数据结构-树

目录

• 树
  • 二叉树
    • 二叉树的生成与遍历(前序遍历法)
  • 线索二叉树的中序建立与遍历
  • 赫夫曼编码

树

二叉树

二叉树的生成与遍历(前序遍历法)

/*
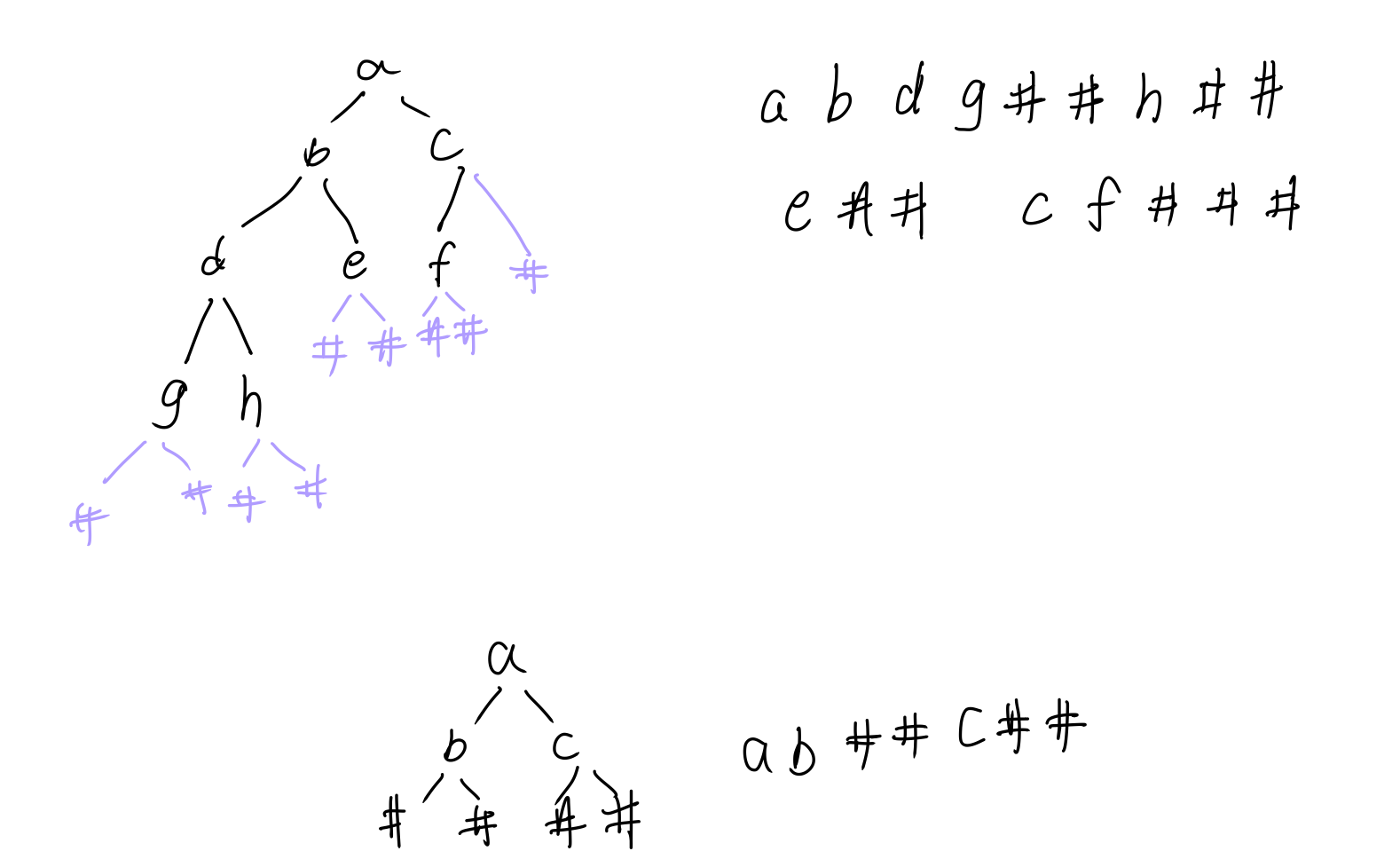
    二叉树
    几个相关的定义：完全二叉树，满二叉树
    二叉树的性质.....需要去了解一下的。

    下面是二叉树的存储于遍历
    使用前序遍历法对输入的数据生成一棵二叉树
    输出某个结点的层数
*/
#include<stdio.h>
#include<stdlib.h>

typedef char elemtype;
typedef struct TNode
{
    elemtype data;
    TNode *lchild ,*rchild;
}TNode,*PTree;

// 传入 一个指向二叉树结点的指针 ，返回一个指向二叉树结点的指针
// 使用前序遍历法创建一棵二叉树
void init_binarytree(PTree *pptree)
{
    char e;
    scanf("%c",&e);
    if(e == '#')
    {
        *pptree = NULL; // 如果输入#表示结点为空
    }
    else
    {
        *pptree = (PTree)malloc(sizeof(TNode));
        (*pptree)->data = e;
        init_binarytree( & (*pptree)->lchild); // 初始化该节点的左子树
        init_binarytree( & (*pptree)->rchild); // 初始化该节点的右子树
    }

}

// 访问成功的操作
void visit(elemtype data, int level)
{
    printf("%c在第%d层\n",data,level);
}

// 遍历操作:前序遍历法
void binarytree_traverse(PTree *pptree,int level)
{
    if(*pptree) // 根节点的访问
    {
        level ++;
        visit((*pptree)->data,level);
        binarytree_traverse( & (*pptree)->lchild,level); // 遍历左子树
        binarytree_traverse( & (*pptree)->rchild,level); // 遍历右子树
    }
}

int main()
{
    int level = 0;
    printf("请按照前序遍历法输入二叉树\n");
    PTree *pptree; // 需要一个指向指针的指针传进去，因为想要修改ptree的值，就要传入指向ptree的指针
    init_binarytree(pptree);
    printf("ptree->data:%c\n",(*pptree)->data);
    binarytree_traverse(pptree,level);

    system("pause");
    return 0;
}

线索二叉树的中序建立与遍历

/*
    线索二叉树
    threaded binary tree

    本质：
        二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构，使每个结点都有了唯一前驱和后继（第一个
    结点无前驱，最后一个结点无后继）。对于二叉树的一个结点，查找其左右子女是方便的，其前驱后继只有在遍历
    中得到。为了容易找到前驱和后继，有两种方法。一是在结点结构中增加向前和向后的指针，这种方法增加了存储
    开销，不可取；二是利用二叉树的空链指针。
*/

# include<stdio.h>
# include<stdlib.h>

typedef char elemtype;
typedef enum {Link,Thread} Pointertag; // Link为0，表示左右孩子存在,Thread为1表示lchild指向前驱，rchild指向后继

typedef struct Tnode
{
    elemtype data;
    Tnode *lchild ,*rchild;
    Pointertag ltag,rtag;
}Tnode,*PTnode;
typedef PTnode *pptnode;
PTnode pre; // 指向上一个遍历结点的指针

// 先前序遍历创建二叉树
void creatbinarytree(pptnode pp)
{
    char e;
    scanf("%c",&e);
    if(e == '#')
    {
        *pp = NULL;
    }
    else
    {
        (*pp) = (PTnode)malloc(sizeof(Tnode));
        (*pp)->data = e;
        (*pp)->ltag = Link;
        (*pp)->rtag = Link;
        creatbinarytree(& (*pp)->lchild);
        creatbinarytree(& (*pp)->rchild);
    }
}
// 中序遍历法使二叉树线索化 这里传入的是根结点
void binarytreethreading(PTnode p)
{
    if(p)
    {
        // 先递归到最低层
        binarytreethreading(p->lchild); // 遍历到一个结点但不访问，留着，先访问它的左子树，然后返回到这里去访问这个结点。中序遍历没毛病
        if( ! p->lchild )
        {
            p->ltag = Thread; // 设置线索状态
            p->lchild = pre; // 设置前驱
        }
        if( ! pre->rchild )
        {
            pre->rtag = Thread; // 设置线索状态
            pre->rchild = p; // 设置前面的结点的后继为此节点 **** 想要设置b结点的一个后继，把b保存在pre中，待到遍历下一个结点c的时候就让pre后继为c 
        }
        pre = p; // 更新pre指针 p成了新的pre
        binarytreethreading(p->rchild); // 线索化右子树
    }
}
// 遍历线索二叉树 对于线索二叉树的遍历，就如同操作一个双向链表,当然也需要一个头结点，可以帮助实现既可以从前往后又可以从后往前遍历
// 初始化一个头结点并完成二叉树线索化 传入根节点
PTnode inittree(PTnode ptree)
{
    PTnode head = (PTnode)malloc(sizeof(Tnode)); // 刚开始忘记给她申请内存了
    head->ltag = Link;
    head->rtag = Thread;
    head->rchild = head; // 先让右子树指向其本身
    PTnode p = ptree; // 根节点
    if( !p ) head->lchild = head; // 如果树为空，则让头结点指向自己
    else
    {
        head->lchild = p;
        pre = head; // pre为头结点
        binarytreethreading(p);
        // 修改末结点的rchild和rtag
        pre->rchild = head;
        pre->rtag = Thread;
        head->rchild = pre; // 将头结点的rchild改成pre
    }

    return head;
}
// 访问操作
void visit(PTnode p)
{
    printf("%c ",p->data);
}

// 中序遍历法遍历线索二叉树链表 传入头结点
void travers_tree( PTnode head )
{
    PTnode p;
    p = head->lchild; 
    while( p != head )
    {
        // 访问左子树
        while(p->ltag == Link)
        {
            p = p->lchild; // 遍历目前这棵树的左子树至最深层
        }
        visit(p);
        
        // 访问走向后继 （这里可以访问某棵树的根节点和右子树，注意，是访问，走向右子树是通过p = p->rchild）
        while(p->rtag == Thread && p->rchild != head) // 没有右子树且后继不是根节点，直接走向后继 
        {
            p = p->rchild;
            visit(p);
        }
        
        p = p->rchild; // 走向右子树
    }
}

int main()
{
    // 初始化一棵二叉树
    PTnode ptree; // 树的根节点
    creatbinarytree(&ptree); // 初始化
    // 设置线索二叉数链表的头结点，并将二叉树线索化
    PTnode head = inittree(ptree);
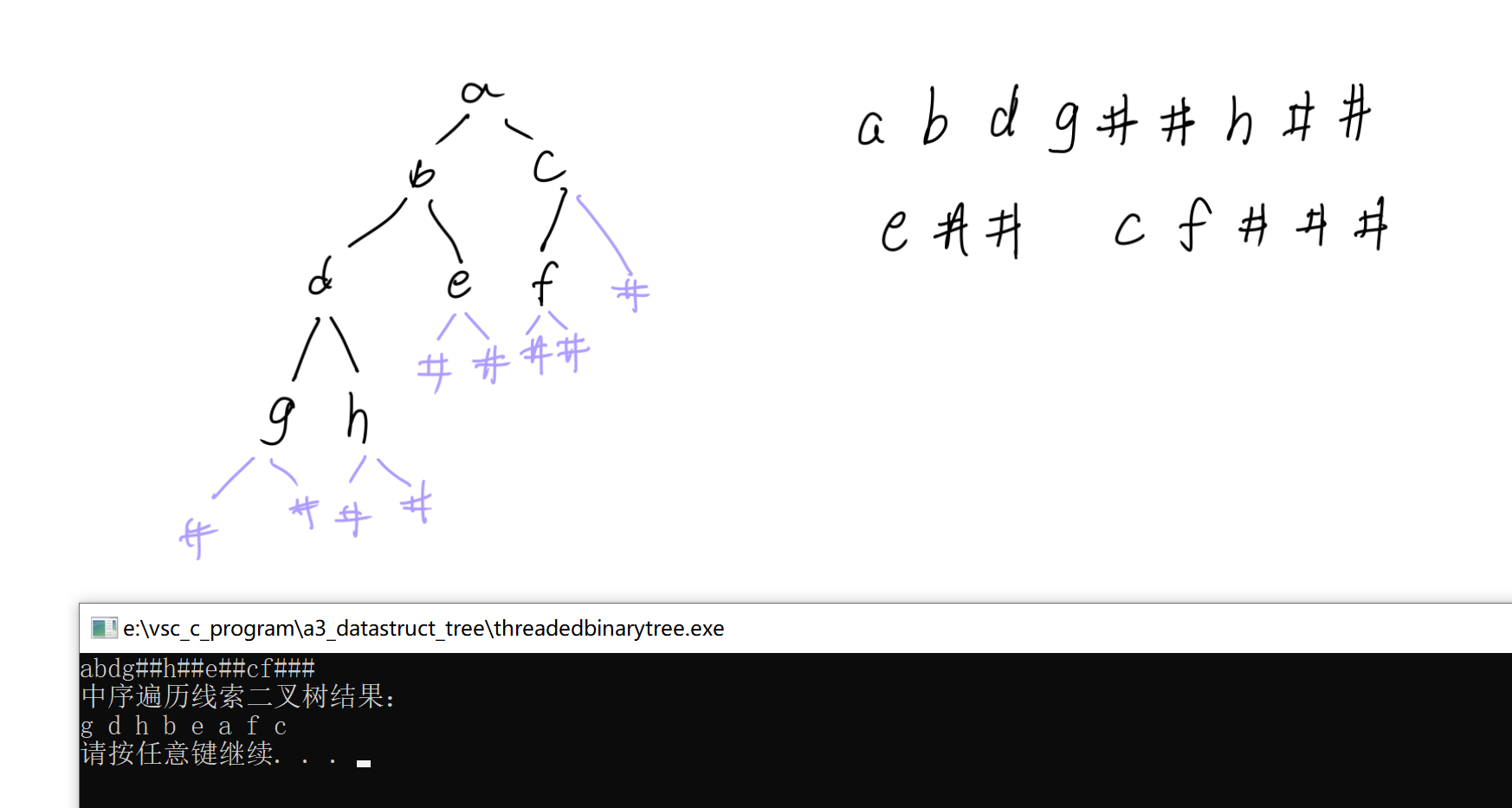
    printf("中序遍历线索二叉树结果：\n");
    travers_tree(head);
    printf("\n");
    system("pause");
    return 0;
}

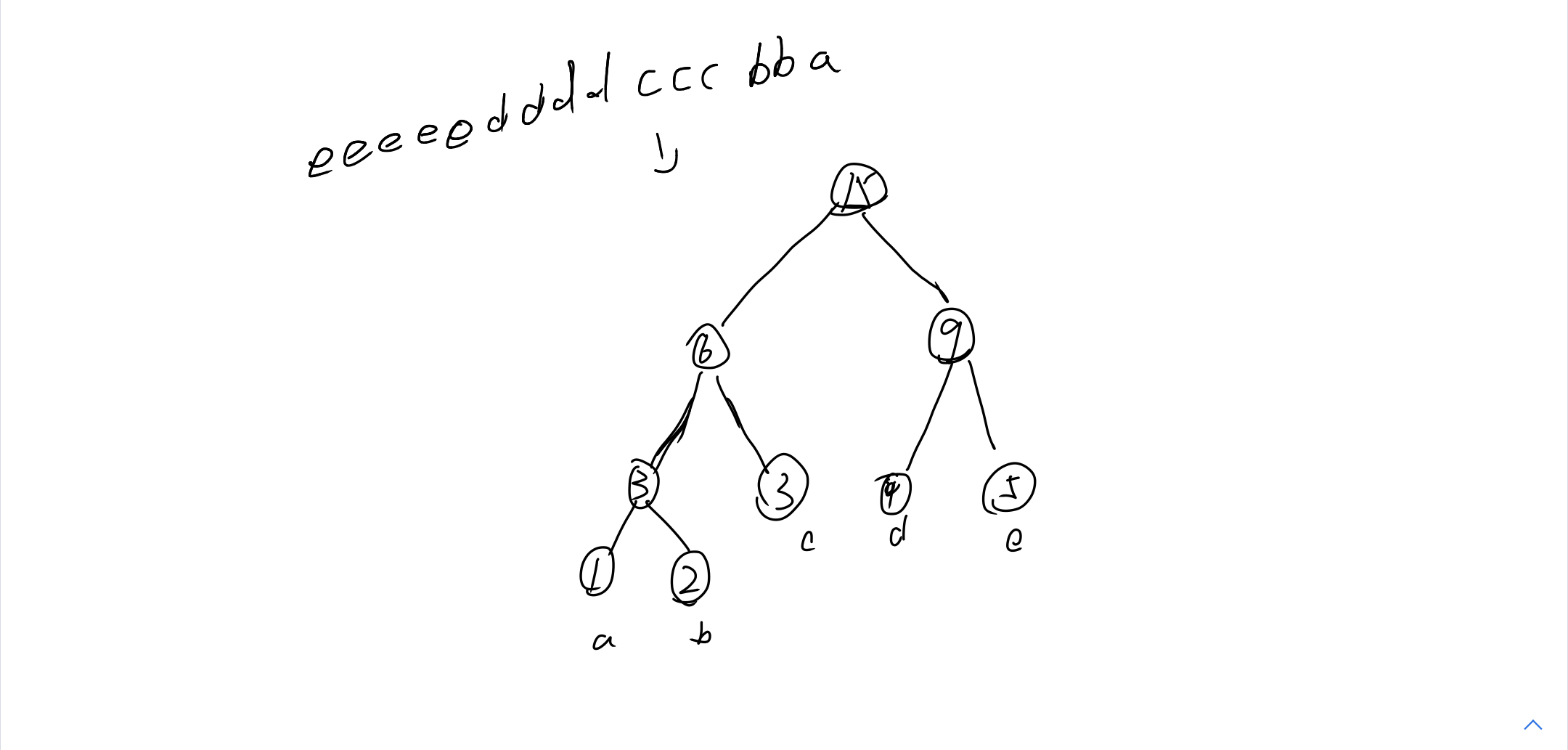
赫夫曼编码

/*
    赫夫曼编码
    1.建立优先级队列
    2.建立赫夫曼树
    3.建立赫夫曼表格
    4.编码encoding
    5.解码decoding
*/
# include<stdio.h>
# include<stdlib.h>
# include<string.h>

// 定义一次性输入的字符串长度的大小
const int MAX_SIZE = 1010;


// 树结构体
typedef struct Tnode
{
    char data ;
    int Weiht ;
    Tnode *lchild,*rchild;
}Tnode,*PTnode;

// 队列结点及其指针的结构体
typedef struct Queue_node
{
    char data ; // 数据域
    int Weight ; // 权值
    Queue_node *next ; // 指针域
    PTnode huftree; // 储存树信息
}Queue_node;
typedef Queue_node *P_quenode; // P_quenode 是指向队列结点的指针

int queue_length;

// 赫夫曼表，对于赫夫曼表，采用链表形式存储
typedef struct Htablenode
{
    char code[256] ; // 一个编码字符串，遍历赫夫曼树产生，左为0右为1
    char data ; // 该编码要代表的数据（字符）
    Htablenode *next;
}Htablenode ,*Phtablenode;

// typedef struct Htable
// {
//     Htablenode *first ; // 保存赫夫曼表的第一个结点
//     Htablenode *last ; // 保存赫夫曼表的最后一个结点
// }Htable;

// 建立优先级队列
/*
    输入一个字符串，统计每个字符串出现的次数为该字符串的权值，权值由小到大放在一个队列里。
    返回一个指向队列头部的指针
    由于后面需要插入和删除等，这里就使用链表结构
*/

// 初始化队列
P_quenode init_queue(char *s)
{
    int cntarr[256]; // 记录出现次数的数组。 每一个字符都可以转换成一个0~255的ascii码
    for(int i = 0 ; i <= 255 ; i ++) cntarr[i] = 0;
    for(int i = 0 ; s[i] != '\0' ; i ++)
    {
        cntarr[s[i]] ++;
    }

    P_quenode head = (P_quenode)malloc(sizeof(Queue_node));
    head->Weight = 0;
    head->next = NULL;
    // 将所有有权值的字符记录进入队列
    for(int i = 0 ; i <= 255 ; i ++)
    {
        if(cntarr[i])
        {
            P_quenode pnode = (P_quenode)malloc(sizeof(Queue_node));
            pnode->data = i ;
            pnode->Weight = cntarr[i];
            pnode->huftree = NULL;
            pnode->next = head->next;
            head->next = pnode;
            queue_length ++;
        }
    }

    return head;
}
// 将队列按权值从小到大排序 冒泡排序
void queue_sort(P_quenode head)
{
    for(int i = 1 ; i <= queue_length - 1; i ++)
    {
        for(int j = 1 ; j <= queue_length - i - 1 + 1; j ++)
        {
            P_quenode p = head ;
            P_quenode q ;
            for(int k = 1 ; k <= j ; k ++) p = p->next; 
            q = p->next;
            if(p->Weight >= q->Weight) 
            {
                P_quenode tmp = (P_quenode)malloc(sizeof(Queue_node));
                *tmp = *q; // 较小的值给tmp
                q->data = p->data;
                q->Weight = p->Weight; // 将大权重的数据存到后面的结点中
                q->huftree = p->huftree;
                p->data = tmp->data;
                p->Weight = tmp->Weight;
                p->huftree = tmp->huftree;
                free(tmp);
            }
        }
    }
}
// 出队与入队
P_quenode queue_out(P_quenode head)
{
    P_quenode outp = head->next;
    head->next = head->next->next;
    outp->next = NULL;
    queue_length --;
    return outp;
}
void queue_in(P_quenode head,P_quenode newnode)
{
    newnode->next = head->next;
    head->next = newnode;
    queue_length ++; // 这里注意先length++再去sort！！！
    queue_sort(head);
}
// 按照权值建立赫夫曼树
PTnode init_huffmantree(P_quenode head)
{
    PTnode T ;
    while(queue_length != 1) // 队列长度为1，就只剩下了根节点
    {
        P_quenode p = queue_out(head);
        P_quenode q = queue_out(head);

        PTnode newtreenode = (PTnode)malloc(sizeof(Tnode));
        newtreenode->lchild = NULL;
        newtreenode->rchild = NULL;
        if(p->huftree && q->huftree)
        {
            newtreenode->lchild = p->huftree;
            newtreenode->rchild = q->huftree;
            newtreenode->Weiht = q->Weight + p->Weight;
        }
        else if(p->huftree || q->huftree)
        {
            if(p->huftree)
            {
                newtreenode->lchild = p->huftree;
                newtreenode->rchild = (PTnode)malloc(sizeof(Tnode));
                newtreenode->rchild->data = q->data;
                newtreenode->rchild->Weiht = q->Weight;
                newtreenode->rchild->lchild = NULL;
                newtreenode->rchild->rchild = NULL;
                newtreenode->Weiht = q->Weight + p->Weight;
            }
            else
            {
                newtreenode->lchild = q->huftree;
                newtreenode->rchild = (PTnode)malloc(sizeof(Tnode));
                newtreenode->rchild->data = p->data;
                newtreenode->rchild->Weiht = p->Weight;
                newtreenode->rchild->lchild = NULL;
                newtreenode->rchild->rchild = NULL;
                newtreenode->Weiht = q->Weight + p->Weight;
            }
        }
        else
        {
            newtreenode->lchild = (PTnode)malloc(sizeof(Tnode));
            newtreenode->rchild = (PTnode)malloc(sizeof(Tnode));
            newtreenode->lchild->data = p->data;
            newtreenode->lchild->Weiht = p->Weight;
            newtreenode->rchild->data = q->data;
            newtreenode->rchild->Weiht = q->Weight;
            newtreenode->lchild->lchild = NULL;
            newtreenode->lchild->rchild = NULL;
            newtreenode->rchild->lchild = NULL;
            newtreenode->rchild->rchild = NULL;
            newtreenode->Weiht = q->Weight + p->Weight;
        }

        free(p);
        free(q);

        P_quenode newqueuenode = (P_quenode)malloc(sizeof(Queue_node));
        newqueuenode->data = newtreenode->data;
        newqueuenode->huftree = newtreenode;
        newqueuenode->Weight = newtreenode->Weiht;
        queue_in(head,newqueuenode);
    }
    P_quenode rootquenode = queue_out(head);
    T = rootquenode->huftree;
    return T;
}

// 建立赫夫曼表
/*
    需要去遍历赫夫曼树，每当遍历左子树就code[k++] = '0'每当遍历右子树就code[k++] = '1'，最后code就是前缀码
    传入一个指向赫夫曼树的头结点
    对表初始化
    遍历赫夫曼树
    返回指向赫夫曼表的指针
*/
// 赫夫曼树遍历函数
/*
    要修改 Phtablenode head,code,idx，就作为参数
*/
void traverse_htree(PTnode T,Phtablenode head,char *code,int idx)
{
    if(T->lchild == NULL && T->rchild == NULL)
    {
        // 遍历到了叶子结点
        code[idx] = '\0' ;
        Phtablenode newnode = (Phtablenode)malloc(sizeof(Htablenode));
        newnode->data = T->data;
        strcpy(newnode->code,code); // 注意这里需要使用字符串复制函数！！！！而且要保证newnode->code足够大
        Phtablenode p = head;
        while(p->next)p = p->next;
        p->next = newnode;
        newnode->next = NULL;
    }
    if(T->lchild != NULL)
    {
        code[idx] = '0';
        traverse_htree(T->lchild,head,code,idx + 1);
    }
    if(T->rchild != NULL)
    {
        code[idx] = '1';
        traverse_htree(T->rchild,head,code,idx + 1);
    }
}

// 解码
void decoding(PTnode T,char *s)
{
    PTnode p = T;
    for(int i = 0 ; s[i] != '\0' ; i ++)
    {
        if(s[i] == '0')
        {
            p = p->lchild;
            if(p->lchild == NULL && p->rchild == NULL)
            {
                printf("%c",p->data);
                p = T;
            }
        }
        else
        {
            p = p->rchild;
            if(p->lchild == NULL && p->rchild == NULL) 
            {
                printf("%c",p->data);
                p = T;
            }
        }
    }
}

Phtablenode init_huffmantable(PTnode T)
{
    Phtablenode head = (Phtablenode)malloc(sizeof(Htablenode));
    head->next = NULL;
    char code[256]; // 用来保存前缀码，256个元素组成二叉树最深为255
    int idx = 0;
    traverse_htree(T,head,code,idx);

    return head;
}


int main()
{
    char s[MAX_SIZE]; 

    scanf("%s",s);
    P_quenode head = init_queue(s);
    P_quenode p = head->next;
    printf("length:%d\n",queue_length);
    queue_sort(head);
    // while(p)
    // {
    //     printf("%c:%d-",p->data,p->Weight);
    //     p = p->next;
    // }
    PTnode T = init_huffmantree(head);
    printf("Huffman树已完成初始化！\n");
    Phtablenode tablehead = init_huffmantable(T);
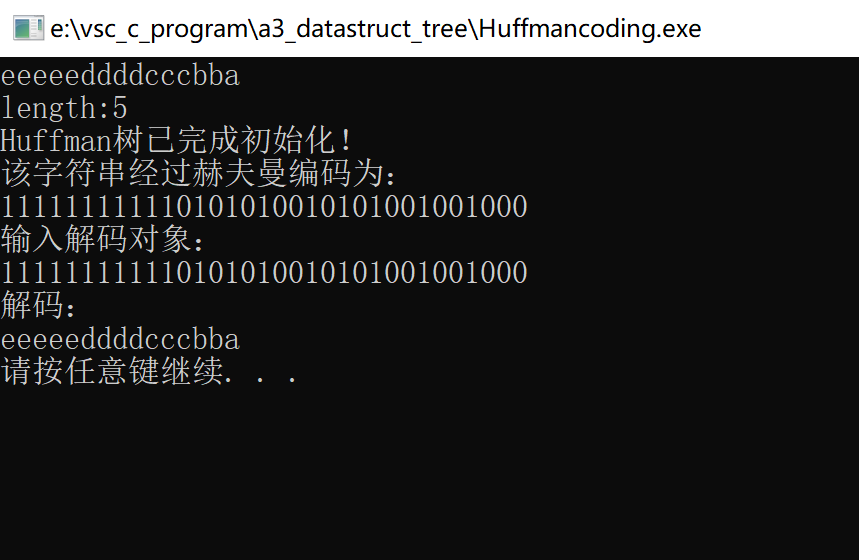
    printf("该字符串经过赫夫曼编码为：\n");
    // 编码
    for(int i = 0; s[i] != '\0'; i ++)
    {
        Phtablenode p = tablehead->next;
        while(p->data != s[i]) p=p->next;
        printf("%s",p->code);
    }
    printf("\n");
    // 解码过程就是按照0/1遍历赫夫曼树，遇到叶子则输出data
    printf("输入解码对象：\n");
    scanf("%s",s);
    printf("解码：\n");
    decoding(T,s);
    printf("\n");

    system("pause");
    return 0;
}