前缀和笔记
前缀和笔记
-
前缀和是一种重要的预处理,能大大降低查询的时间复杂度。可以简单理解为“数列的前 \(n\) 项的和”。
-
C++ 标准库中实现了前缀和函数
std::partial_sum,定义于头文件<numeric>中。
一维前缀和
简介
一维前缀和顾名思义
就是一维的前缀和
前缀和是什么呢?
前缀和就是到目前为止全部的和是多少
一维就是单纯的一串数
他的前缀和就成了一维前缀和
举例
\(1\space2\space3\space4\space5\space6\)
他的前缀和依次就是 \(1\space3\space6\space10\space15\space21\)
\(i\) 位置上的前缀和就是从第一个数到第 \(i\) 个数全部数的和
这样就很显然的知道了什么是一维前缀和了吧?
例题
输入 #1
7
2 -4 3 -1 2 -4 3
输出 #1
4
参考代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn = 200010;
int a[maxn],s[maxn];
int n;
int main(){
cin>>n;
for (int i = 1;i <= n ; i ++ ) cin>>a[i];
for (int i = 1; i <= n ; i ++ ) {
s[i]=s[i-1]+a[i];
}
int ans = -2e9 ,mn = s[0];
for (int r = 1; r <= n ; r ++ ) {
ans = max(ans,s[r]-mn);
mn = min(mn,s[r]);
}
cout<<ans<<endl;
return 0;
}
二维前缀和
简介
二维前缀和顾名思义
就是二维的前缀和
二维很显然了
有 \(x\) 轴和 \(y\) 轴也就是一个面
这很显然
那二维前缀和中一个 \(f[i][j]\) 表示的意思就是
以 \((1,1)\) 为左上角以 \((i,j)\) 为右下角这个矩阵里面数的和
如图
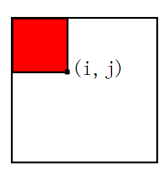
\(f[i][j]\)表示的就是图中红色的部分

二维前缀和求矩阵元素和
二维前缀和可以用来干什么呢?
一维前缀和你可以用来 \(O(1)\) 求某个点的值
那么类比一下
二维前缀和也是可以用来求某个矩阵的值的
但是怎么来求呢?
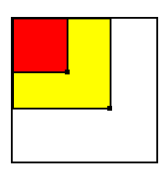
就如图中
知道了两个点的位置和他们的二维前缀和
图中红色是左上角的那个点的二维前缀和
红色+黄色部分是右下角的那个点的二维前缀和
是不是可以用这个来求出他们之间的矩阵的和呢?
也就是这一部分:
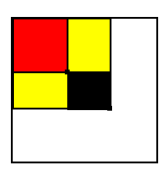
图中黑色的部分就是我们要求的那个矩阵和
是不是可以通过某些奇怪的方法求出黑色部分是多少?
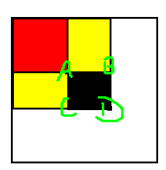
-
\(D\) 点表示的二维前缀和值是红色部分+两个黄色部分+黑色部分
-
\(A\) 点表示的是红色部分
-
\(B\) 点表示的是上面的黄色部分+红色部分
-
\(C\) 点表示的是下面的黄色部分+红色部分
这里面只有 \(D\) 的前缀和里面包括黑色部分
只要减去 \(D\) 里面的哪两个黄色部分和红色部分是不是就剩下了我们要求的黑色部分了?
那怎么减去呢?
可以这样:\(D-B-C+A\)
这就是二维前缀和最重要的部分了
化成二维数组的形式就是这样的
为什么上文成立
继续看上面那张图
由 \(D-B-C+A\) 到方程式这个很显然所以就不多说了
只要证明出 \(D-B-C+A\) 是正确的那就没有问题了
这个可以化成:
红色部分+上面的黄色部分+下面的黄色部分+黑色部分-上面的黄色部分-红色部分-下面的黄色部分-红色部分+红色部分
这样是不是很巧妙的就只剩下了黑色部分
所以成立
二维前缀和怎么求
这个可以类比上面求矩阵的思想
只是这个矩阵的右下角是 \((i,j)\) ,左上角也是
\((i,j)\)
就是一个 \(1\times1\) 的矩阵
所以也是很好求的
但是上面是已知 \(D,A,B,C\) 求黑色部分
这里你只知道 \(A,B,C\) 和黑色部分
因为是一个 \(1\times1\) 的矩阵嘛
所以黑色部分就只有一个元素也就是 \((i,j)\) 坐标上的那个元素值
所以就可以个加法变减法,减法变加法一个性质的
通过 \(A,B,C\) 和黑色部分来求出 \(D\)
- \(D\) 点表示的二维前缀和值是红色部分+两个黄色部分+黑色部分
- \(A\) 点表示的是红色部分
- \(B\) 点表示的是上面的黄色部分+红色部分
- \(C\) 点表示的是下面的黄色部分+红色部分
所以 \(D\) 就可以等于 \(B+C-D\space+\) 黑色部分:
上面的黄色部分+红色部分+下面的黄色部分+红色部分-红色部分+黑色部分
=上面的黄色部分+红色部分+下面的黄色部分+黑色部分
刚好等于 \(D\),方程式为
例题
在一个 \(n\times m\) 的只包含 \(0\) 和 \(1\) 的矩阵里找出一个不包含 \(0\) 的最大正方形,输出边长。
输入 #1
4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1
输出 #1
2
参考代码:
#include <algorithm>
#include <iostream>
using namespace std;
int a[103][103];
int b[103][103]; // 前缀和数组,相当于上文的 f[]
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
b[i][j] =
b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1] + a[i][j]; // 求前缀和
}
}
int ans = 1;
int l = 2;
while (l <= min(n, m)) { //判断条件
for (int i = l; i <= n; i++) {
for (int j = l; j <= m; j++) {
if (b[i][j] - b[i - l][j] - b[i][j - l] + b[i - l][j - l] == l * l) {
ans = max(ans, l); //在这里统计答案
}
}
}
l++;
}
cout << ans << endl;
return 0;
}
作业
求最大矩阵和
输入 #1
4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
输出 #1
15
输出 #1解释
9 2
-4 1
-1 8
\(ACcode:\)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 500;
int a[maxn][maxn],s[maxn][maxn],p[maxn];
int n;
int getarea(int p[]) {
int mn = min(p[1],0),sum = p[1],mx=-2e9;
for (int i = 2; i <= n ; i ++ ) {
sum+=p[i];
mx=max(mx,sum-mn);
mn=min(mn,sum);
}
return mx;
}
int main(){
cin>>n;
for (int i = 1; i <= n ; i ++ ) {
for (int j = 1; j <= n ; j ++ ) {
cin>>a[i][j];
s[i][j]=s[i-1][j]+a[i][j];
}
}
int ans = -2e9;
for (int d = 1; d <= n ; d ++ ){
for (int i = d ; i <= n ; i ++ ) {
for (int j = 1 ; j <= n ; j ++ ) p[j] = s[i][j]-s[i-d][j];//构造一维的情况
ans=max(ans,getarea(p));
}
}
cout<<ans<<endl;
return 0;
}


