NOIP 2000 进制转换
题目描述 t1.cpp/in/out
我们可以用这样的方式来表示一个十进制数： 将每个阿拉伯数字乘以一个以
该数字所处位置的（值减１）为指数，以１０为底数的幂之和的形式。例如：
１２３可表示为 １＊１０２＋２＊１０１＋３＊１００这样的形式。
与之相似的，对二进制数来说，也可表示成每个二进制数码乘以一个以该数
字所处位置的（值－１）为指数，以２为底数的幂之和的形式。一般说来，任
何一个正整数Ｒ或一个负整数－Ｒ都可以被选来作为一个数制系统的基数。如
果是以Ｒ或－Ｒ为基数，则需要用到的数码为 ０，１，．．．．Ｒ－１。例
如，当Ｒ＝７时，所需用到的数码是０，１，２，３，４，５和６，这与其是
Ｒ或－Ｒ无关。如果作为基数的数绝对值超过１０，则为了表示这些数码，通
常使用英文字母来表示那些大于９的数码。例如对１６进制数来说，用Ａ表示
１０，用Ｂ表示１１，用Ｃ表示１２，用Ｄ表示１３，用Ｅ表示１４，用Ｆ表
示１５。
在负进制数中是用－Ｒ 作为基数，例如－１５（十进制）相当于１１０００１
（－２进制），并且它可以被表示为２的幂级数的和数：
１１０００１＝１＊（－２）５＋１＊（－２）４＋０＊（－２）３＋０＊
（－２）２＋
０＊（－２）１ ＋１＊（－２）０
设计一个程序，读入一个十进制数和一个负进制数的基数, 并将此十进制数转
换为此负进制下的数： －Ｒ ∈ ｛－２，－３，－４，．．．，－２０｝
输入
输入的每行有两个输入数据。
第一个是十进制数Ｎ（－32768 ＜＝Ｎ＜＝32767 ）； 第二个是负进制数的基
数－Ｒ。
输出
结果显示在屏幕上，相对于输入，应输出此负进制数及其基数，若此基数
超过１０，则参照１６进制的方式处理。
样例输入
30000 -2
样例输出
30000=11011010101110000 （base -2
***将10进制转换成n进制，这里需要用短除法。将10进制数取余n，其商再继续取余直到该数被除至0，依次得到的余数倒序即为该10进制数的n进制表示。如果将10进制转换为-n进制呢？方法基本一样，只不过要注意的是要使其余数>=0，绝对不能为负数。举个例子，将10进制数15转换成-2进制：
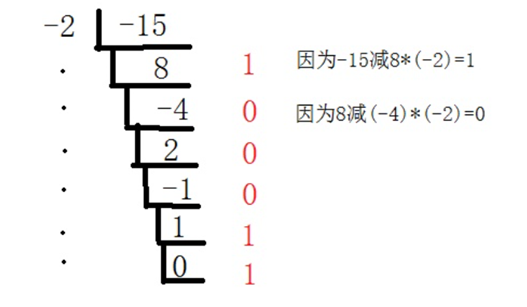
因为由于除法是向0取整的，所以余数有可能是负的(例如(-15)%(-2)=-1)。为了余数为非负整数且满足余数小于n。当余数为负数时，我们可以将商++后重新计算余数，就会发现它变成非负的了。
