jieba 分词改进(1)
在前面的 jieba 分词源代码研读系列中,提出了一个问题即结巴分词对于未登录词的分词表现有待改进。所谓工欲善其事,必先利其器。在探寻解决之道前,我们先研究一下HMM三大算法中的最后一个:向前-向后算法。这个算法解决的问题是 在已经知道输出序列和状态序列后找出一个最匹配的HMM模型即HMM的学习问题。
顾名思义 向前-向后算法中的向前即前向算法。而向后算法也和前向算法类似,不同点在于后向算法在初始化时,把状态概率设为1,而且计算的顺序与序列顺序相反。详见:http://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-2。
前向算法提供了一个基于 t 时刻之前的序列的局部概率 a(i),而后向算法提供了基于 t 时刻之后的序列的局部概率 b(i),其中 i表示这时候处于 状态 i。把这两个概率相乘就能得到 向前-向后算法中 某时刻 t 系统处于状态 i 的概率了(其实更准确的理解应该是 t+1时刻 的状态来自 t时刻 状态i的转变的概率,这也解释了为什么后向算法中把初值即序列的最后时刻的各个状态概率都设为1。在公式中会除以一个分母这是为了归一化),称为 r(i) 。在 t 时刻系统处于状态 i ,而在 t+1 时刻系统处于 状态 j 的概率则等于:
ξ(i , j) = a(i) * T( j | i) * E( o | j ) * b( j)
其中a(i) 表示 t 时刻系统处于状态 i 的概率,而 T( j | i) 表示转移概率,E( o | j )表示 t+1时刻状态 j 输出为 o 的发射概率,b( j)表示 t+1 时刻处于状态 j 的后向概率 ,当然在公式中为了归一化要除以一个分母,这里省略。详见:http://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-4
于是有:

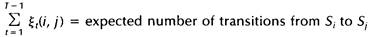

下面的代码我是用python实现的一个向前向后算法:
# -*- coding: utf-8 -*-
# python2.7
import math
MIN_FLOAT=-3.14e100
class BaumWelch:
#参数列表:输出序列,状态序列,初始的状态分布概率,初始的状态转换概率,初始的发射概率
def __init__(self, out_seq, hidden_seq, states, prob_start, prob_trans, prob_emit, maxIterNum=20):
self.seq = zip(list(out_seq), list(hidden_seq))
self.states = tuple(states)
self.prob_start = prob_start
self.prob_trans = prob_trans
self.prob_emit = prob_emit
self.maxIterNum = maxIterNum
self.forward_net = {}
self.backward_net = {}
def log(self, value):
if value == 0:
return MIN_FLOAT
else:
return math.log(value)
def buildnet(self):
if self.forward_net is None or len(self.forward_net.keys()) == 0:
for t, sw in enumerate(self.seq):
prob_t = {}
for s in self.states:
if t == 0:
prob_t[s] = self.prob_start[s]+self.prob_emit[s].get(sw[0], MIN_FLOAT)
else:
emit_p = self.prob_emit[s].get(sw[0], MIN_FLOAT)
prob_t[s] = self.log(sum([math.e**(self.forward_net[t-1][s0] + self.prob_trans[s0].get(s, MIN_FLOAT) + emit_p) for s0 in self.states]))
self.forward_net[t] = prob_t
if self.backward_net is None or len(self.backward_net.keys()) == 0:
T = len(self.seq)-1
for i in range(T, -1, -1):
prob_t = {}
if i == T:
#后向算法的初值设置,T表示序列的最后一个时刻
prob_t = dict([(s, 1) for s in self.states])
else:
for s in self.states:
prob_t[s] = self.log(sum([math.e**(self.backward_net[i+1][s1]+self.prob_trans[s].get(s1, MIN_FLOAT)+self.prob_emit[s1].get(self.seq[i+1][0], MIN_FLOAT)) for s1 in self.states]))
self.backward_net[i] = prob_t
def forward(self, seq, states):
"""
获取某一个时刻序列的前向局部概率
"""
if self.forward_net is not None and 0 in self.forward_net.keys():
return self.forward_net[len(seq)-1]
prob_t = {}
for i, sw in enumerate(seq):
if i == 0:
for s in states:
prob_t[s] = self.prob_start[s]+self.prob_emit[s].get(sw[0], MIN_FLOAT)
else:
buf = dict(prob_t)
for s in states:
emit_p=self.prob_emit[s].get(sw[0], MIN_FLOAT)
prob_t[s] = self.log(sum([math.e**(buf[s0]+self.prob_trans[s0].get(s,MIN_FLOAT)+emit_p) for s0 in self.states]))
return prob_t
def backward(self, seq, states):
"""
获取某一个时刻序列的后向局部概率
"""
if self.backward_net is not None and 0 in self.backward_net.keys():
return self.backward_net[len(seq)-1]
prob_t = {}
T = len(seq)-1
for i in range(T, -1, -1):
if i == T:
#后向算法的初值设置,T表示序列的最后一个时刻
prob_t = dict([(s, 1) for s in states])
else:
#print i
buf = dict(prob_t)
for s in states:
prob_t[s] = self.log(sum([math.e**(buf[s1]+self.prob_trans[s].get(s1, MIN_FLOAT)+self.prob_emit[s1].get(seq[i+1][0], MIN_FLOAT)) for s1 in states]))
return prob_t
def getr(self, seq, t, states):
"""
获取t时刻的前向局部概率和后向局部概率的乘积并归一化,即r概率
"""
prob_t = {}
sum = 0.0
for s in states:
prob_forward = self.forward(seq[0:t+1], states)
prob_backward = self.backward(seq[t:], states)
prob_t[s] = prob_forward[s] + prob_backward[s]
sum += math.e**prob_t[s]
buf = dict(prob_t)
for s in states:
if math.e**buf[s] == 0.0:
prob_t[s] = MIN_FLOAT
else:
if math.e**buf[s] == 0.0:
prob_t[s] = MIN_FLOAT
else:
prob_t[s] = self.log((math.e**buf[s])/sum)
return prob_t
def getxi(self, seq, t, states):
"""
获取t时刻的ξ概率
"""
xi = {}
sum = 0.0
T = len(seq)
for s in states:
xi[s] = 1
if t == T-1:
return None
prob_forward = self.forward(seq[0:t+1], states)
prob_backward = self.backward(seq[t:T], states)
#print t, prob_backward
for s in states:
for s1 in states:
tmp = (s, s1)
xi[tmp] = prob_forward[s]+prob_backward[s1]+self.prob_trans[s].get(s1,MIN_FLOAT)+self.prob_emit[s1].get(seq[t+1][0],MIN_FLOAT)
sum += math.e**xi[tmp]
buf = dict(xi)
for s in states:
for s1 in states:
tmp = (s,s1)
if math.e**buf[tmp] == 0.0:
xi[tmp] = MIN_FLOAT
else:
xi[tmp] = self.log(math.e**buf[tmp]/sum)
return xi
def doEM(self):
while self.maxIterNum > 0:
#E
self.buildnet()
seq_r = {}
seq_xi = {}
for i, sw in enumerate(self.seq):
seq_r[i] = self.getr(self.seq, i, self.states)
seq_xi[i] = self.getxi(self.seq, i, self.states)
#M
self.updatePI(seq_r, self.states)
self.updateTrans(seq_r, seq_xi, self.states)
self.updateEmit(self.seq, seq_r, self.states)
if self.ErrorIsOk(self.seq):
break
self.maxIterNum -= 1
def updatePI(self, seq_r, states):
"""
更新初始概率
"""
for s in states:
self.prob_start[s] = seq_r[0][s]
def updateTrans(self, seq_r, seq_xi, states):
"""
更新状态转移概率
"""
for s in states:
sum_r=0.0
for t in range(0,len(seq_r)-1):
sum_r+=math.e**seq_r[t][s]
for s1 in states:
sum_xi=0.0
for t in range(0,len(seq_r)-1):
sum_xi += math.e**seq_xi[t][(s, s1)]
self.prob_trans[s][s1] = self.log(sum_xi/sum_r)
def updateEmit(self, seq, seq_r, states):
"""
更新发射概率
"""
for s in states:
sum_r = 0.0
state_output={}
for t in range(0,len(seq_r)):
sum_r+=math.e**seq_r[t][s]
state_output.setdefault(seq[t][0],0.0)
state_output[seq[t][0]] += math.e**seq_r[t][s]
for o in state_output.keys():
self.prob_emit[o] = self.log(state_output[o]/sum_r)
def ErrorIsOk(self,seq):
"""
判断误差是否小于要求
"""
prob, path = self.viterbi([s[0] for s in self.seq], self.states, self.prob_start, self.prob_trans,self.prob_emit)
print prob, path
for state_viterbi in path:
for right in seq:
if right[0] != state_viterbi:
return False
return True
def viterbi(self,obs, states, start_p, trans_p, emit_p):
V = [{}]
path = {}
for y in states:
V[0][y] = start_p[y] + emit_p[y].get(obs[0], MIN_FLOAT)
path[y] = [y]
for t in range(1, len(obs)):
V.append({})
newpath = {}
for y in states:
em_p = emit_p[y].get(obs[t], MIN_FLOAT)
(prob, state) = max([(V[t-1][y0] + trans_p[y0].get(y, MIN_FLOAT) + em_p, y0) for y0 in states])
V[t][y] = prob
newpath[y] = path[state] + [y]
path = newpath
(prob, state) = max([(V[len(obs) - 1][y], y) for y in states])
return prob, path[state]
这个算法实现的思路很明确。有了这个算法我们就可以训练自己的语料库了。同时也可以看看 jieba 分词给出的概率在不停迭代后会是一个什么结果呢???



 浙公网安备 33010602011771号
浙公网安备 33010602011771号