一道算法题的想法

题目：

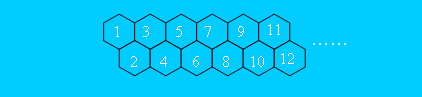
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。 其中，蜂房的结构如下所示。

思路：

题目要求我们计算任意两“蜂巢”之间可能的路线总数，不妨先简化一下题目：

从1 号蜂巢出发，计算到任意蜂巢之间可能的路线。

为方便理解，再用特殊例子简化题目：

计算从1 号蜂巢出发，到5 号蜂巢的可能的路线。

像走迷宫一样，我们从1 号蜂巢开始穷举，得到很多路线：

1-> 2-> 3-> 4-> 5;

1-> 2-> 3-> 5;

1-> 2-> 4-> 5;

…….

显然这样是很麻烦的，不妨从终点蜂巢开始往前思考：

5 号蜂巢的来路只有4 号和3 号蜂巢；

4 号蜂巢的来路只有3 号和2 号蜂巢；

3 号蜂巢的来路只有2 号和1 号蜂巢；

…...

这样我们很容易总结出：

n 号蜂巢的来路只有n-1号和n-2号蜂巢。

这样，我们可以得到：

到5 号蜂巢的路线之和 = 到4 号蜂巢路线之和 + 到3 号蜂巢路线之和

到4 号蜂巢的路线之和 = 到3 号蜂巢路线之和 + 到2 号蜂巢路线之和；

…...

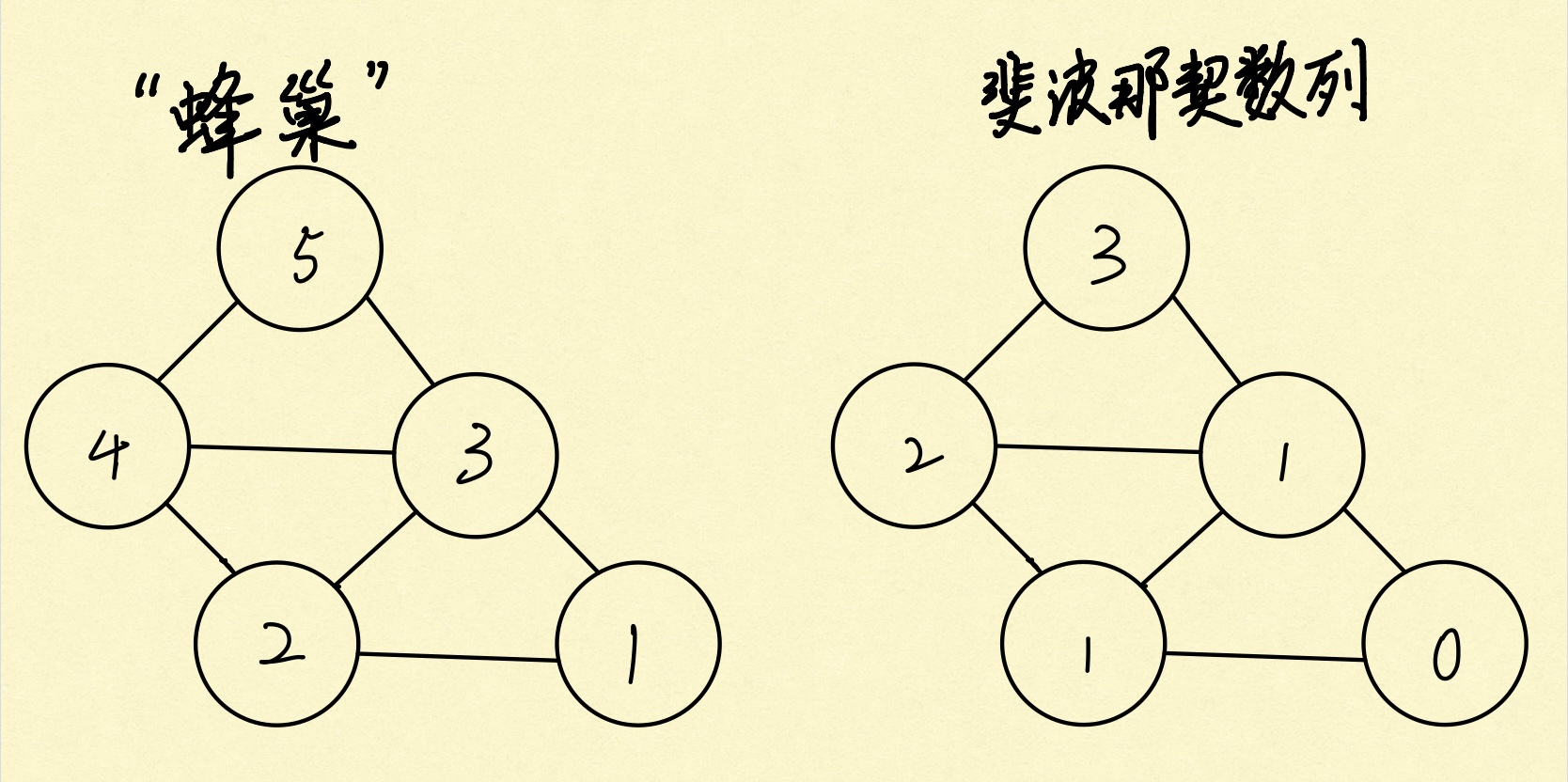
这个模型很容易让我们联想到斐波那契数列，经过验证，我们可以发现当1 号蜂巢和2 号蜂巢作为前两项时，它们的来路总数分别是1 和1，与斐波那契数列的第1、2 项相吻合。将该结论推广，可以得到：

从1 号蜂巢出发到n 号蜂巢可能路线总数 = 斐波那契数列的第n 项。

将以上结论再推广到“任意选择起点”的情况，我们就很容易解决原问题：

从m 号蜂巢出发到n 号蜂巢可能路线总数 = 斐波那契数列的第n-m+1 项。

这样，我们要解决的问题就转化成了求斐波那契数列的任意项问题。

代码实现：

斐波那契数列的代码实现有很多种方式，最简单易懂的莫过于从斐波那契数列的定义出发，用递归的方法计算。

int Fibonacci(int n) {
  if (n == 0)
    return 0;
  if (n == 1)
    return 1;
  else
    return Fibonacci(n - 1) + Fibonacci(n - 2);
}

当n 的值很大时，递归算法将多次重复调用Fibonacci 函数，导致运算速度缓慢。我们将寻求一种新的算法。我将它称为一种类似于“车厢”的模型。

从链表到“车厢”模型

当我们学习数据结构时，我们用代码实现了链表的遍历，其原理是将一个中间结点变量反复赋值，这个中间结点变量就是一个“单节运算车厢”，它执行 -> next 这个运算来寻找下一个结点。

bool List() {
  Node *tempnode = Person_List;
  for(; tempnode-> next != NULL; ) {
    tempnode = tempnode->next;
  }
}

而在计算斐波那契数列时，我们需要一个“双节运算车厢”来执行加法运算，设定两个中间变量first_node 和second_node ，在循环体中对其进行反复赋值，从而得出第n 个斐波那契数列项。

int RouteSum(int n) {
  int first_node = 0;
  int second_node = 1;
  int node_total;
  for (int i = 0; i < n - 1; ++i) {
  	node_total = first_node + second_node;
  	first_node = second_node;
  	second_node = node_total;
  }
  return node_total;
}

以此类推，当我们需要一次计算更多项时就需要更多节的“运算车箱”，而“车厢”内执行的运算类型也可以灵活改变。

解题代码

#include <iostream>

using namespace std;

int RouteSum(int start_node, int end_node) {
  int node_difference = end_node - start_node;
  int first_node = 0;
  int second_node = 1;
  int node_total;
  for (int i = 0; i < node_difference; ++i) {
  	node_total = first_node + second_node;
  	first_node = second_node;
  	second_node = node_total;
  }
  return node_total;
}

int main() {
  int m,n;
  cin >> m;
  cin >> n;
  cout << RouteSum(m,n);
}