方差、标准差、协方差、相关系数

【方差】

　　（variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。方差是衡量源数据和期望值相差的度量值。（百度百科）

　　

　　在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式：

　　            

　　实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，样本方差计算公式：

　　S^2= ∑(X-  ) ^2 / (n-1)     S^2为样本方差，X为变量，  为样本均值，n为样本例数。（无偏估计）

【标准差】

　　标准差（Standard Deviation） ，中文环境中又常称均方差，是离均差平方的算术平均数的平方根，用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。标准差也被称为标准偏差，或者实验标准差，公式为

　　  

【协方差】

　　可以通俗的理解为：两个变量在变化过程中是同方向变化，还是反方向变化，同向或反向程度如何？

　　你变大，同时我也变大，说明两个变量是同向变化的，这时协方差就是正的。

　　你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的。

　　从数值来看，协方差的数值越大，两个变量同向程度也就越大。反之亦然。

　　

　　公式简单翻译一下是：如果有X,Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值，（其实是求“期望”，但就不引申太多新概念了，简单认为就是求均值了）。

【相关系数】

　　相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。由于研究对象的不同，相关系数有如下几种定义方式。简单相关系数：又叫相关系数或线性相关系数，一般用字母r 表示，用来度量两个变量间的线性关系。

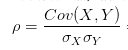　　　　就是用X、Y的协方差除以X的标准差和Y的标准差。 所以，相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差。

　　既然是一种特殊的协方差，那它：

　　1、也可以反映两个变量变化时是同向还是反向，如果同向变化就为正，反向变化就为负。

　　2、由于它是标准化后的协方差，因此更重要的特性来了：它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。

 【参考文献】

https://www.zhihu.com/question/20852004

https://baike.baidu.com/item/%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0/3109424?fr=aladdin

https://blog.csdn.net/u010182633/article/details/45921929

https://www.zhihu.com/question/20099757