numpy方法介绍
三、numpy系列




1、np.maximum:(X, Y, out=None)
X 与 Y 逐位比较取其大者;
最少接收两个参数
h=[[-2,2,10],[-5,-9,20]]
hh=np.maximum(h, 1)
hh=[[1,2,10],[1,1,20]]
2、np.max:(a, axis=None, out=None, keepdims=False)
求序列的最值
最少接收一个参数
axis:默认为列向(也即 axis=0),axis = 1 时为行方向的最值;
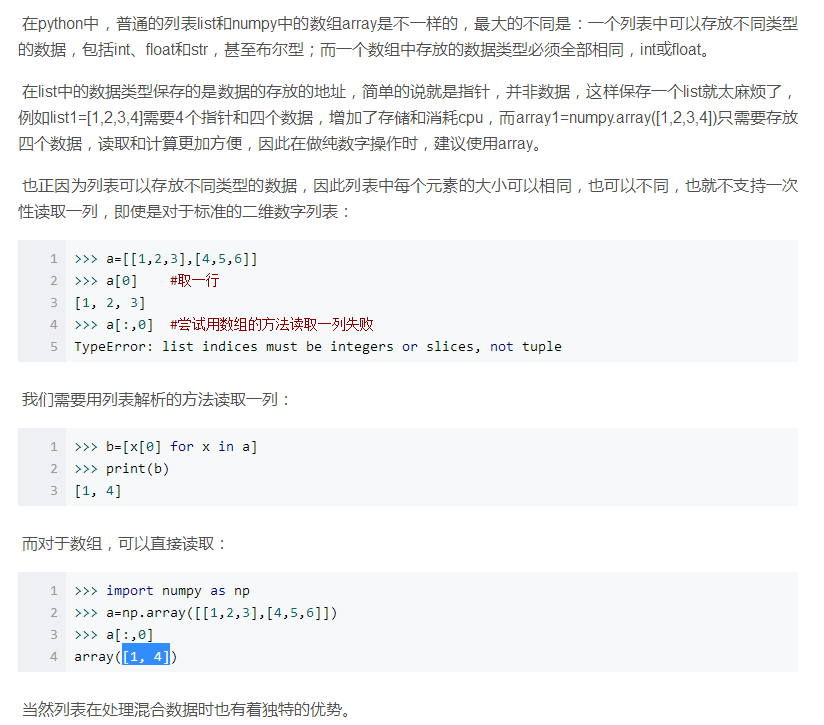
3、np.array([[1,2,3],[4,5,6]])
创建np数组
a[:,0] 输出结果为[1, 4]
4、np.linspace(-5,5,200)[:,np.newaxis];,
生成线性随机x数据,数据-5到5,总共200个
5、np.random.normal(0,0.5,x_data.shape);
生成0-0.5高斯分布的 x_data.shape类型的数据
6、矩阵变换、变形
a.reshape(-1) a.reshape(3, 4, -1) a.T # 转置 a.transpose() # 转置
numpy.linalg.inv(a) # 求逆
a.diagonal([offset, axis1, axis2]) #对角元
numpy.einsum('iijj->ij',a) numpy.r_[a,b] # 在a中增加新行b numpy.c_[a,b] # 新列
7、一般运算
y = x # 建立引用,修改x会影响y
y = x.copy() # 建立副本,修改x不会影响
y a.dot(b) # 矩阵乘法
numpy.dot(a,b) # 矩阵乘法 numpy.trace(a) #求迹
8、特殊矩阵
a = numpy.zeros([4,5]) # all zero
a = numpy.ones([7,6]) # all one
a = numpy.eye(4,7) # 4x7 diagonal 对角线
a = numpy.diag(range(5)) # 5x5 diagonal 对角线
a = numpy.empty((2,3))
a = numpy.arange(10, 30, 5) # array([10, 15, 20, 25]), 1-D
a = numpy.linspace(0, 2, 9) # 9 numbers from 0 to 2
a = numpy.random.random((2,3)) # 随机数矩阵
a = numpy.fromfunction(f,(5,4),dtype=int) # 从函数f(x,y)建立
9、numpy.tile(A,reps)
tile共有2个参数,A指待输入数组,reps则决定A重复的次数。整个函数用于重复数组A来构建新的数组。
假设reps的维度为d,那么新数组的维度为max(d,A.ndim)。下面分三种情况进行讨论:
(1)A.dim < d
则向A中添加新轴扩充A的维度。维度大小可以从shape中看出,一般通过向shape对应的元组中添加1完成对A维度的扩充。扩充完成后,则可根据reps的值对A中相应维度的值进行重复。例如,一维数组shape为(3,),扩充至2维则shape值为(1,3),扩充至3维则shape值为(1,1,3)
(2)A.dim > d
将reps扩充至与A相同的维度。扩充方法同上,也是向shape对应元组中添1,然后再进行重复。例如,4维数组A的shape为(2,3,4,5),而reps为(2,2)只有2维,那么就要对reps添维进行扩充,得到(1,1,2,2)
(3)A.dim = d
不需要扩充,直接按reps的值对相应维度的值进行重复。
>>>from numpy import * >>> a = array([1,2,3]) >>>print a.shape (3.) >>>print a.ndim 1 >>>b = tile(a,2) >>>print b [1 2 3 1 2 3] >>>print b.shape (6,) >>>print b.ndim 1 >>>c = tile(a,(2,3)) >>>print c [[1 2 3 1 2 3 1 2 3] [1 2 3 1 2 3 1 2 3]] >>>print c.shape (2,9) >>>print c.ndim 2

