20202316 2021-2022-1 《数据结构与面向对象程序设计》实验九报告
# 20202316 2021-2022-1 《数据结构与面向对象程序设计》实验九报告
课程:《程序设计与数据结构》
班级: 2023
姓名: 饶坤
学号:20202316
实验教师:王志强
实验日期:2021年12月18日
必修/选修: 必修
## 1.实验内容
(1) 初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)(2分)
(2) 图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)(4分)
(3) 完成有向图的拓扑排序,并输出拓扑排序序列或者输出该图存在环(3分)
(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出(3分)
(5) 完成有向图的单源最短路径求解(迪杰斯特拉算法)(3分)
## 2. 实验过程及结果
(1)初始化:根据屏幕提示(例如:输入1为无向图,输入2为有向图)初始化无向图和有向图(可用邻接矩阵,也可用邻接表),图需要自己定义(顶点个数、边个数,建议先在草稿纸上画出图,然后再输入顶点和边数)
我画的有向图和无向图如下:
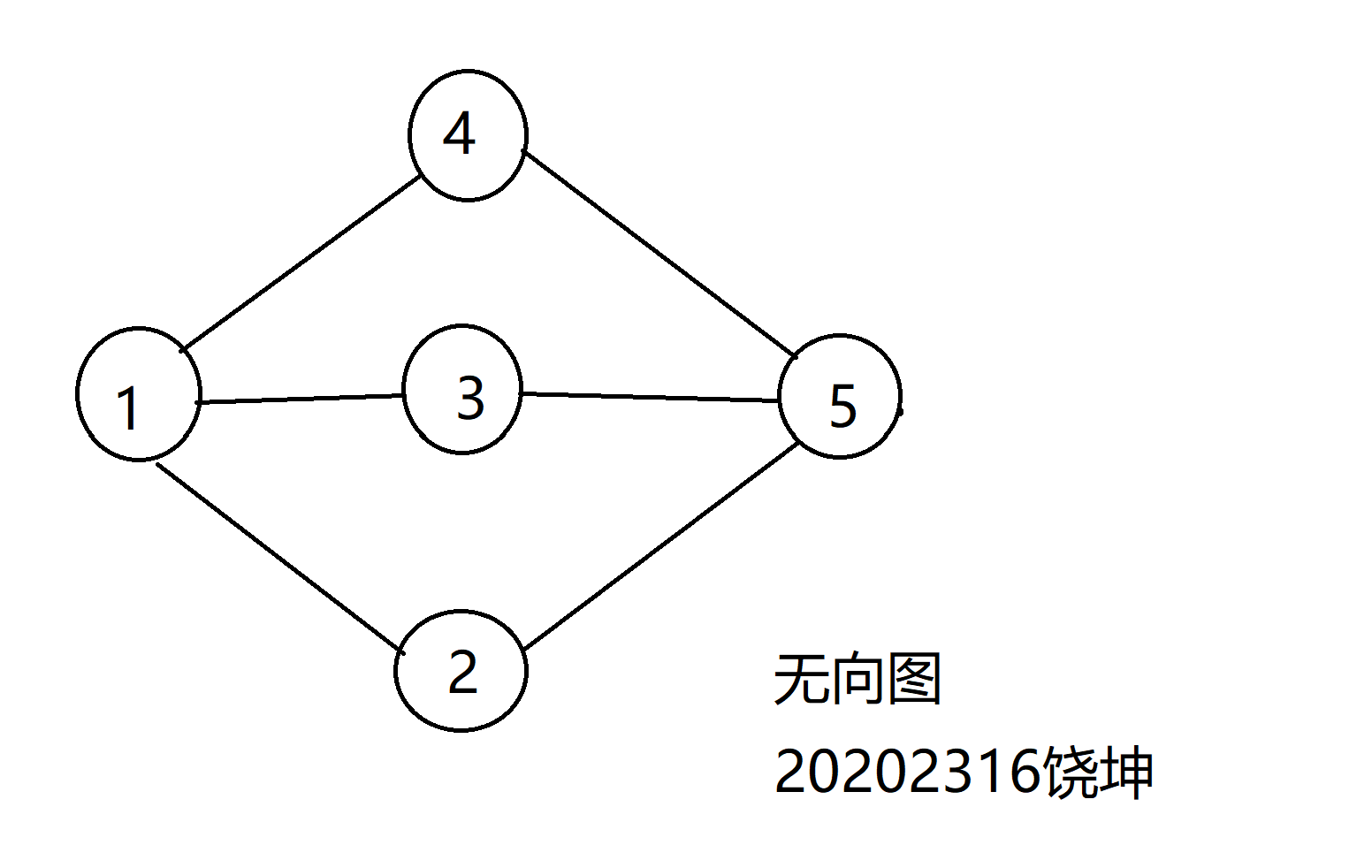
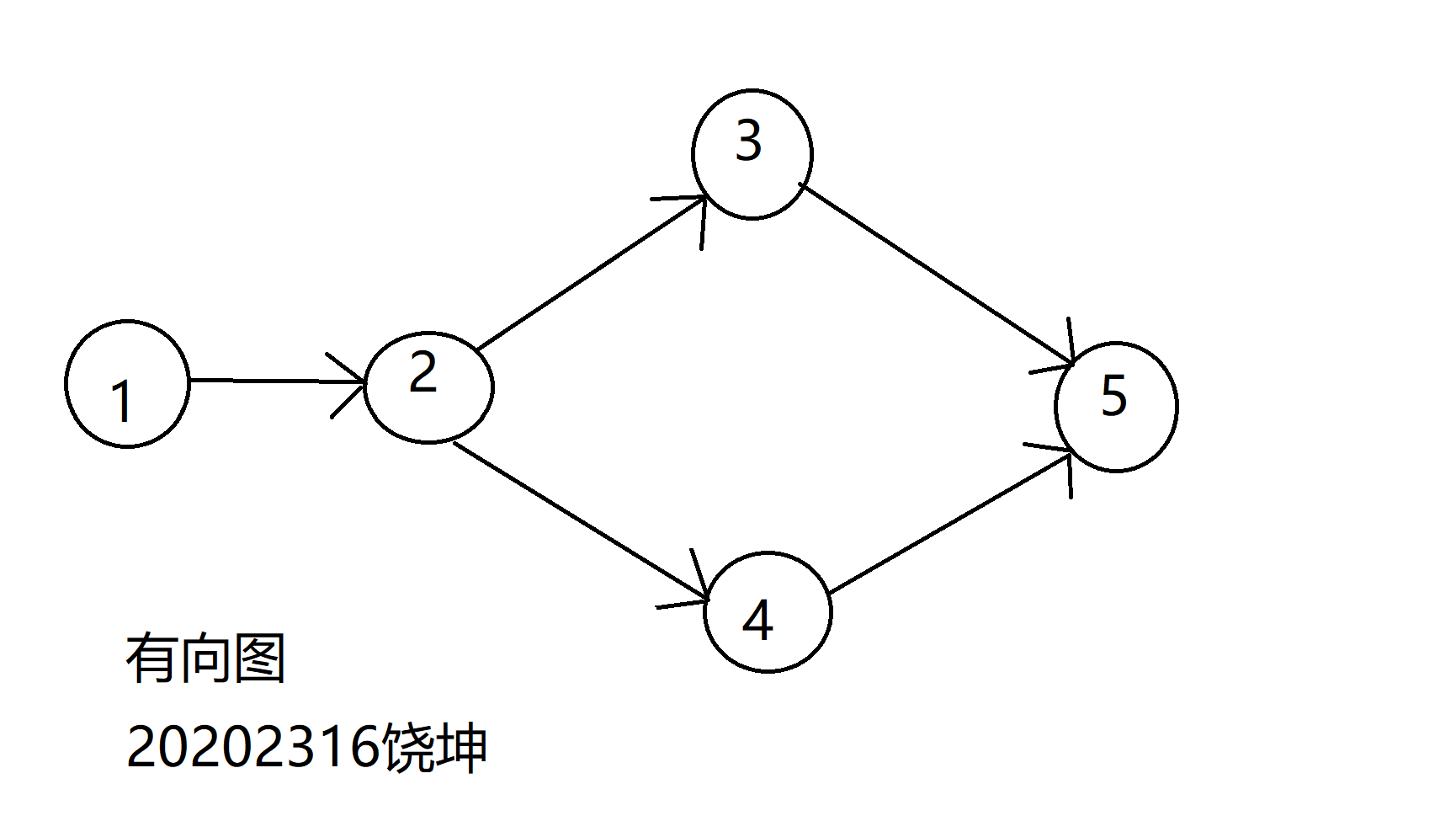
无向图和有向图的代码以及矩阵的建立:
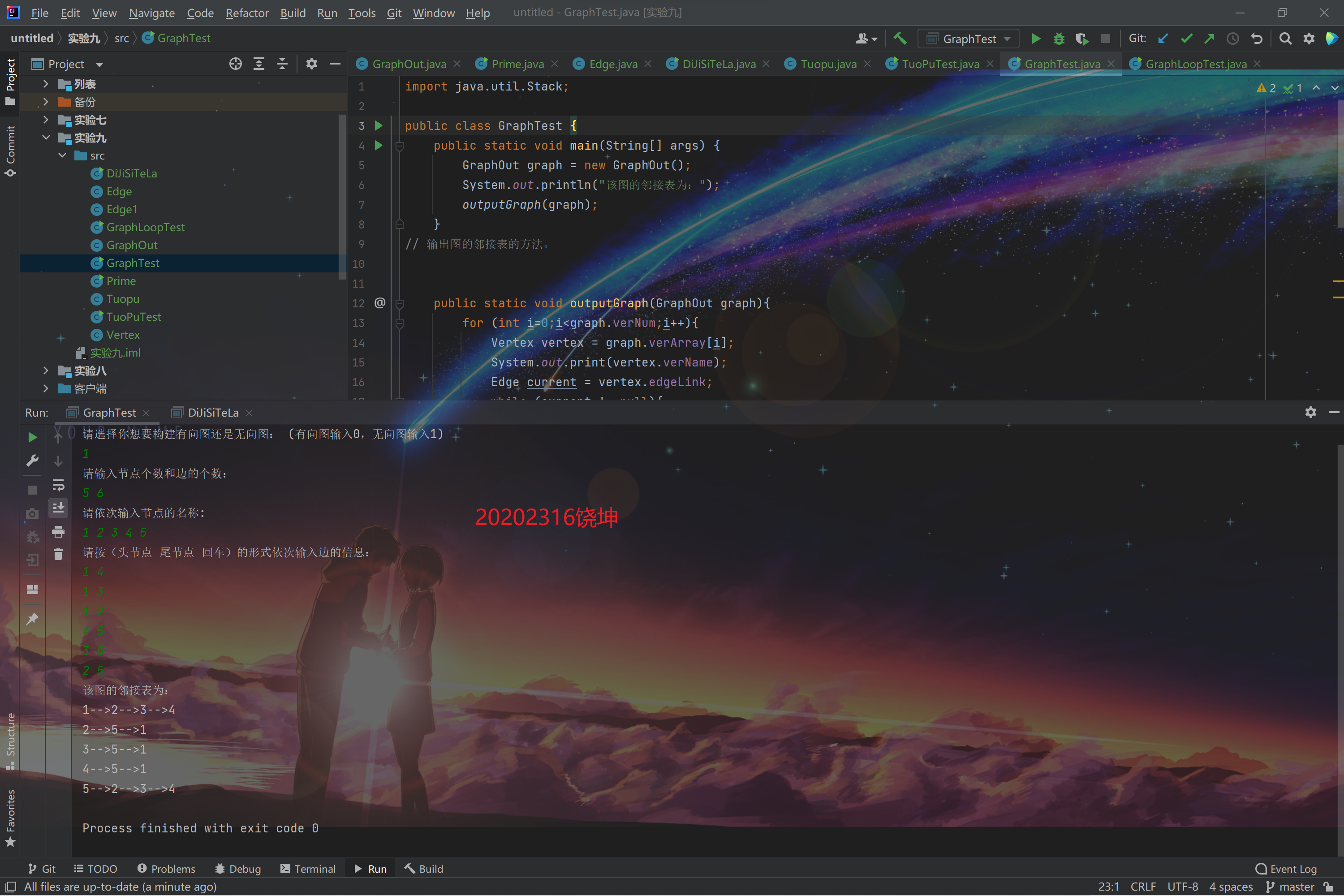
运行结果
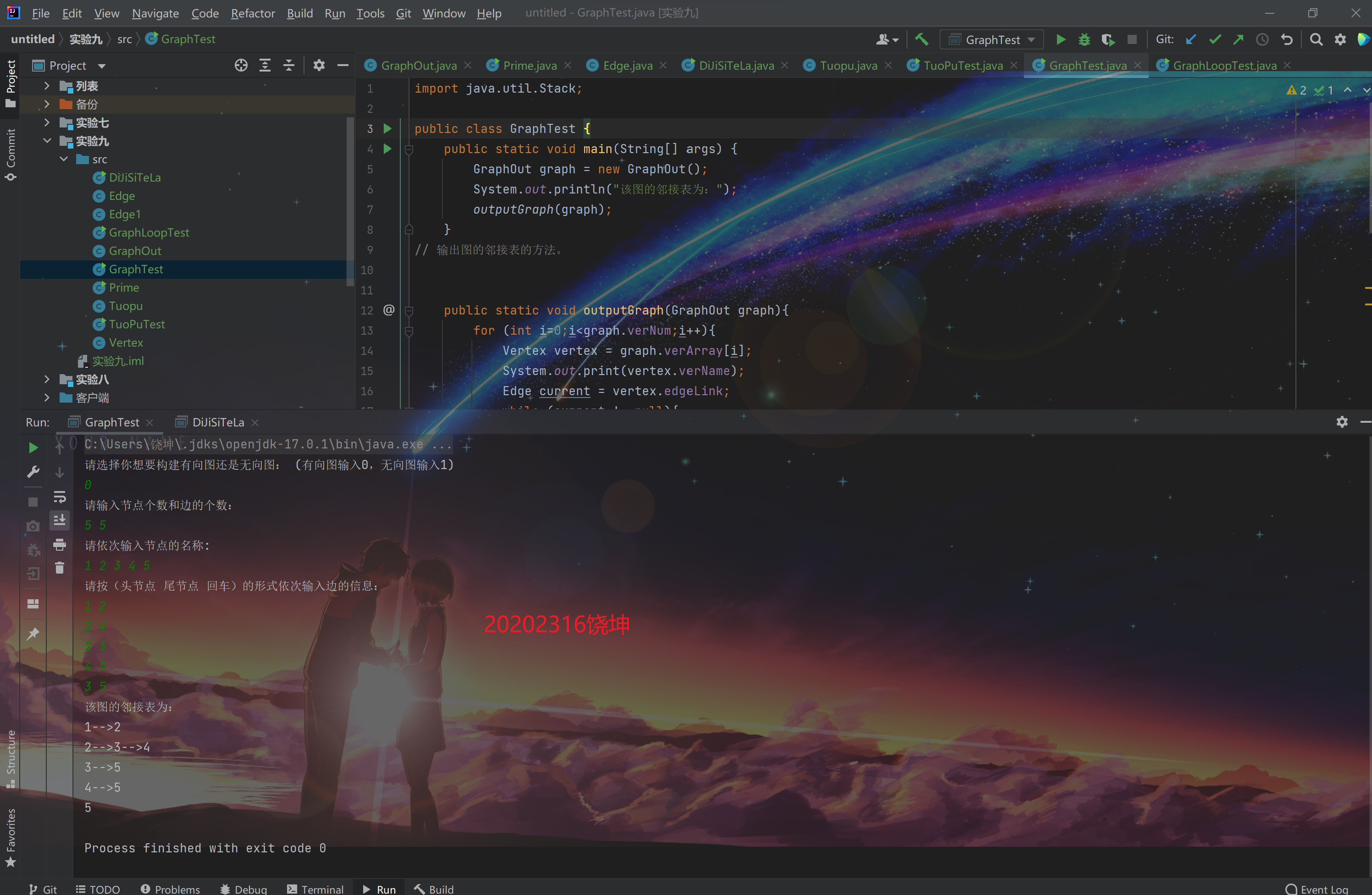
(2)图的遍历:完成有向图和无向图的遍历(深度和广度优先遍历)
图:
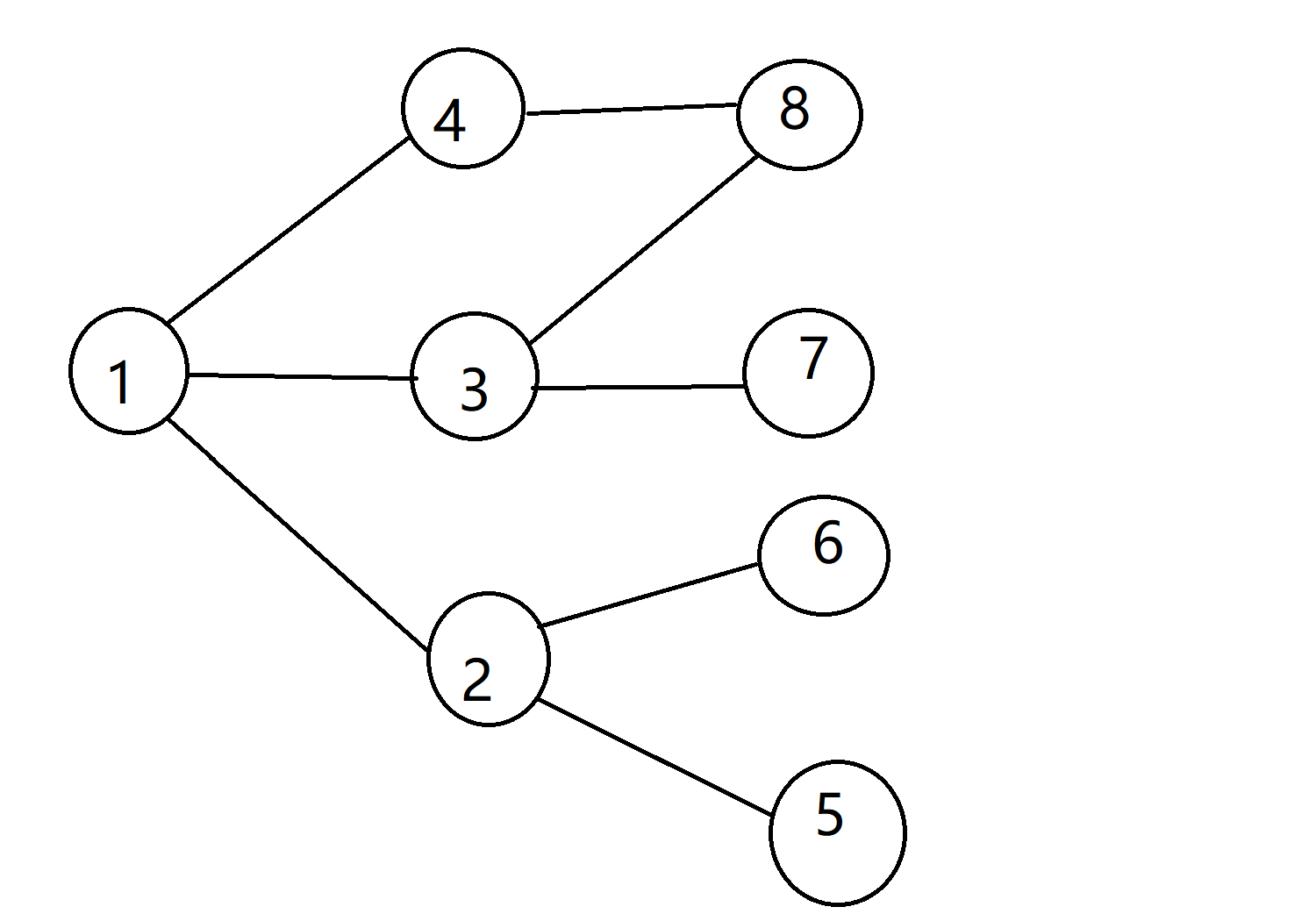
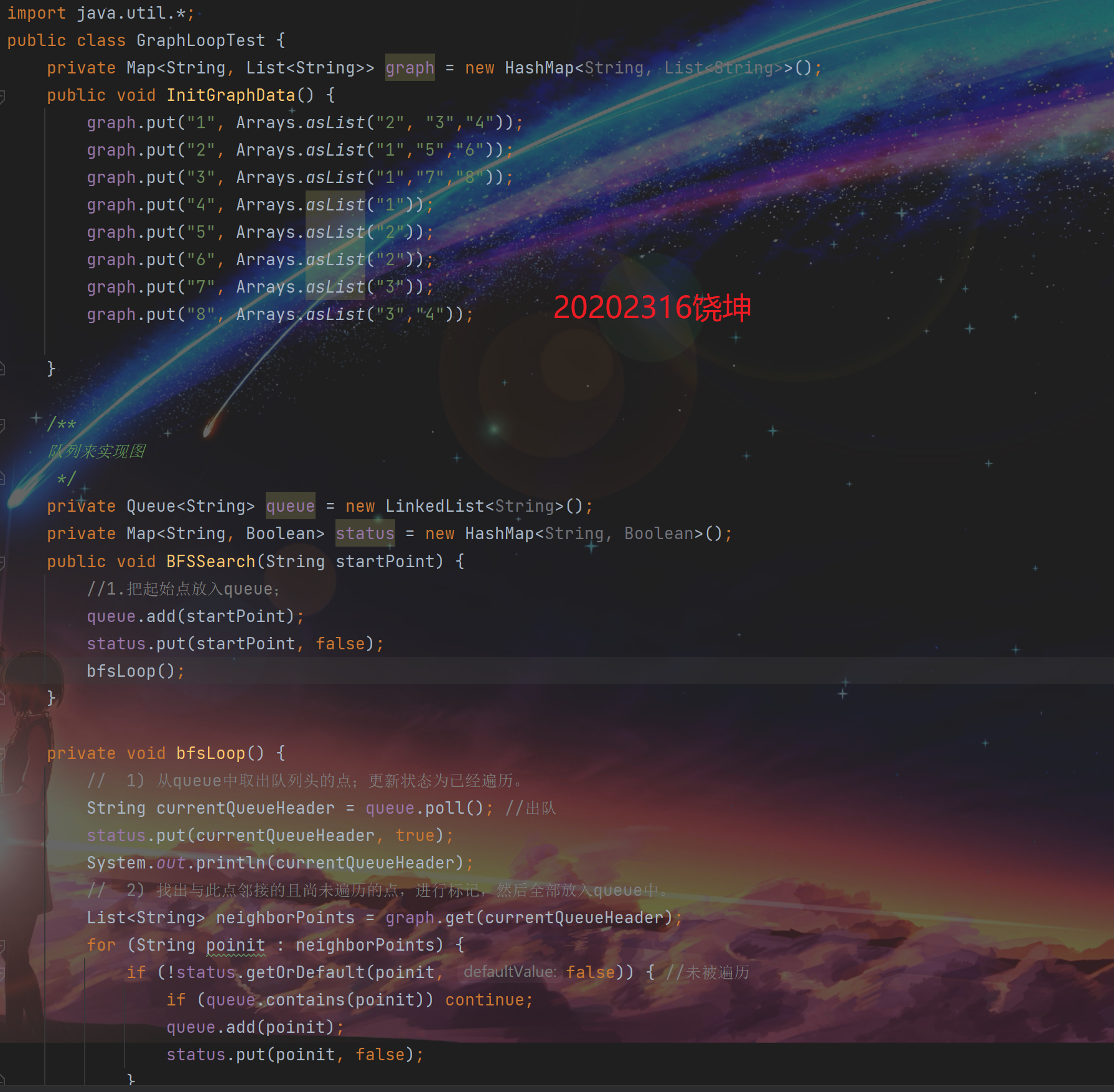
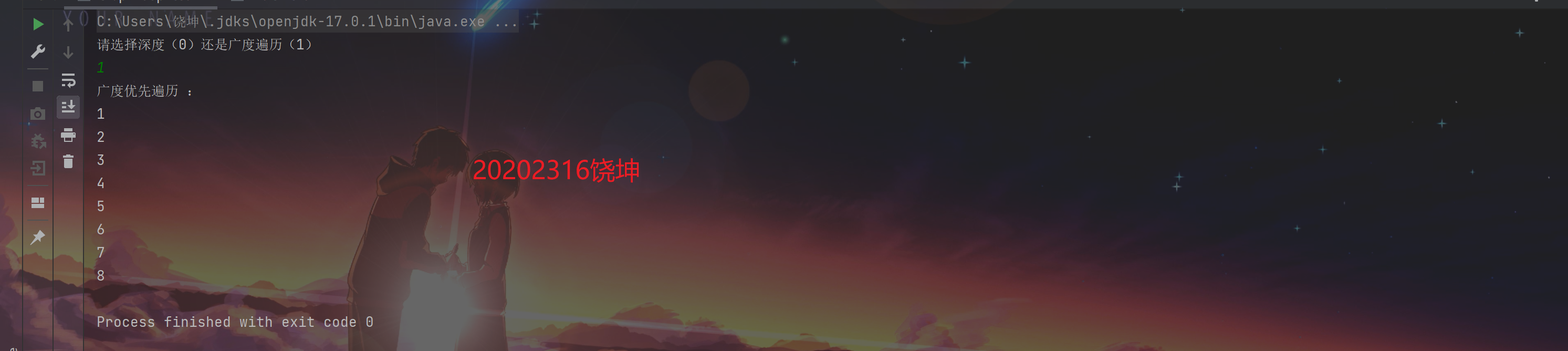
运行的广度优先遍历和深度优先遍历

(3) 有向图的拓扑排序
在有向图中选一个没有前驱的顶点并且输出
从图中删除该顶点和所有以它为尾的弧(白话就是:删除所有和它有关的边)
重复上述两步,直至所有顶点输出,或者当前图中不存在无前驱的顶点为止,后者代表我们的有向图是有环的,因此,也可以通过拓扑排序来判断一个图是否有环
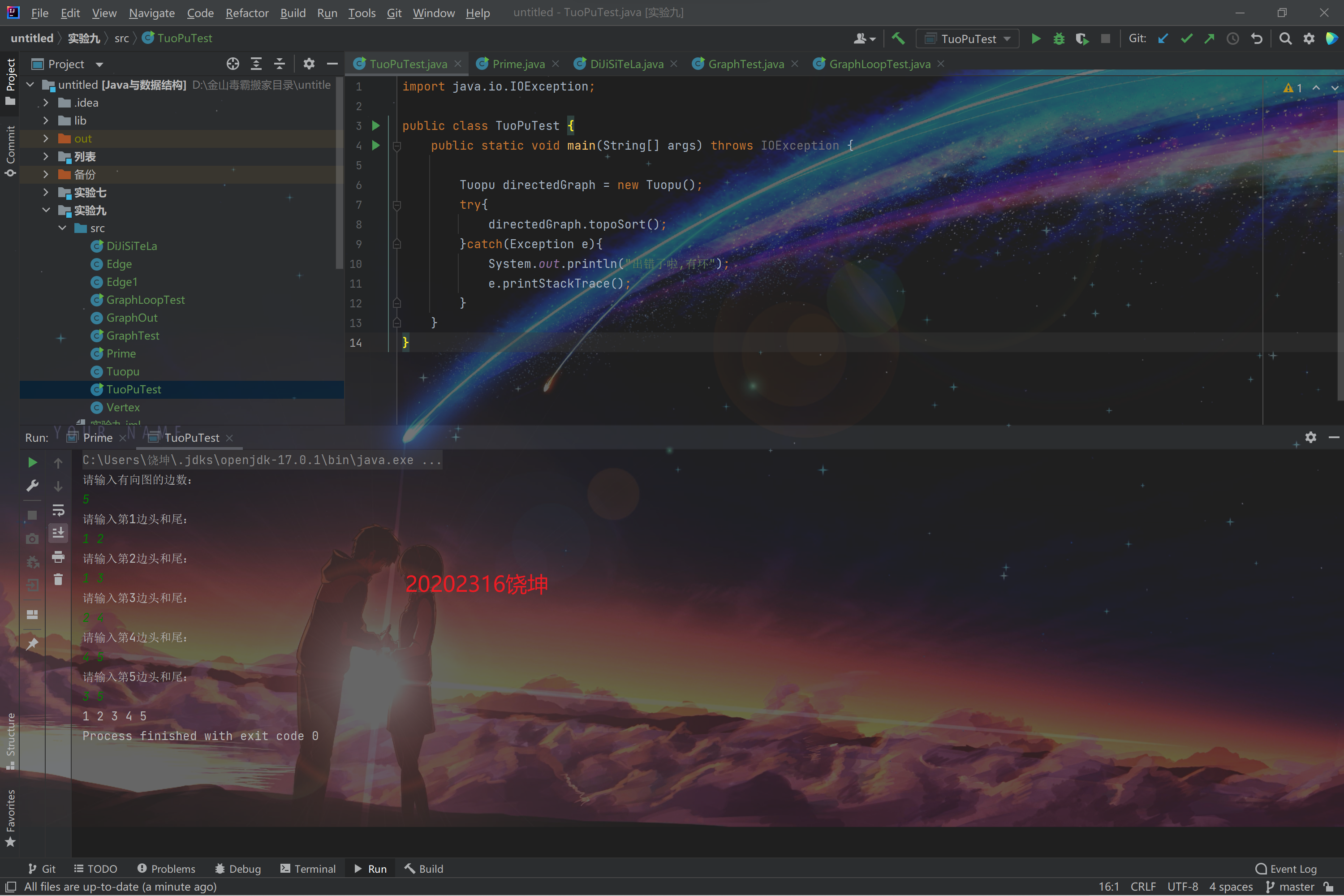
有环的情况

(4) 完成无向图的最小生成树(Prim算法或Kruscal算法均可),并输出。
- 最小生成树的构造方法共有两种:Kruskal与Prim算法
- 在这里我用的是prim算法
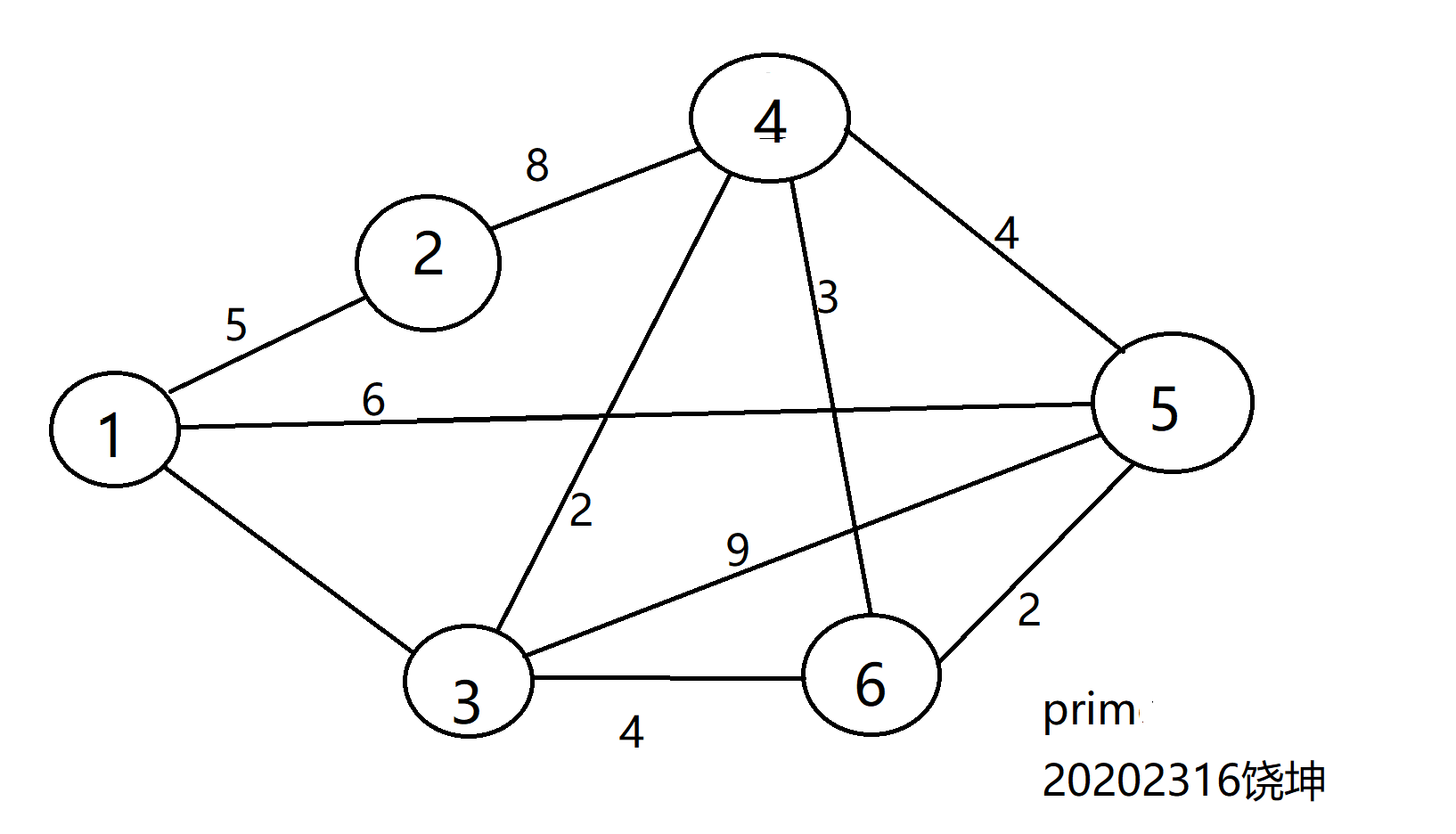
代码及运行情况
相对应的矩阵
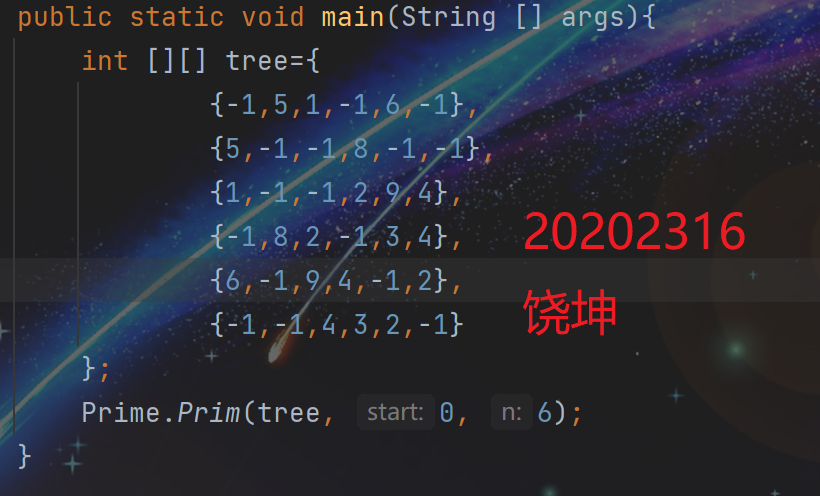
代码运行
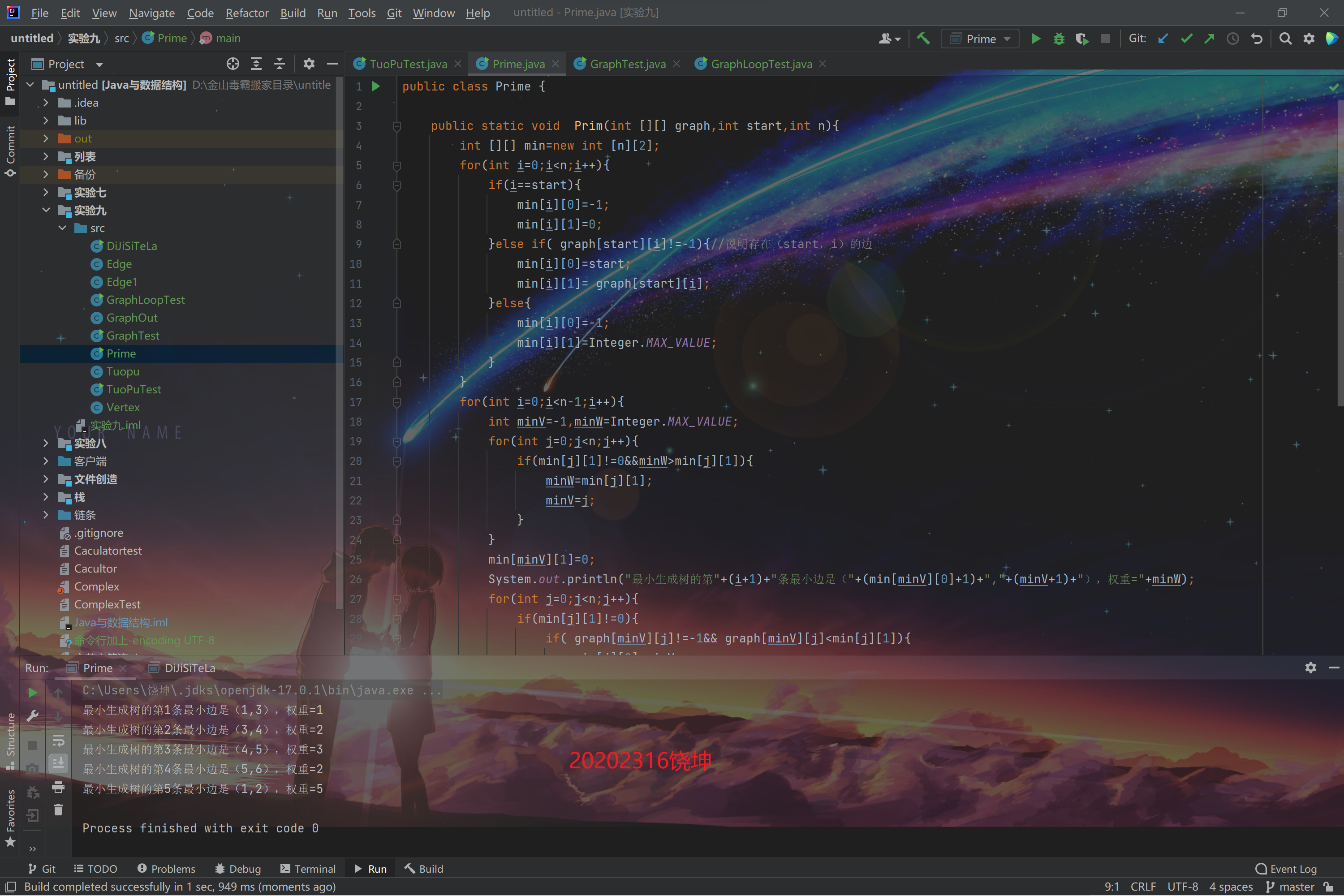
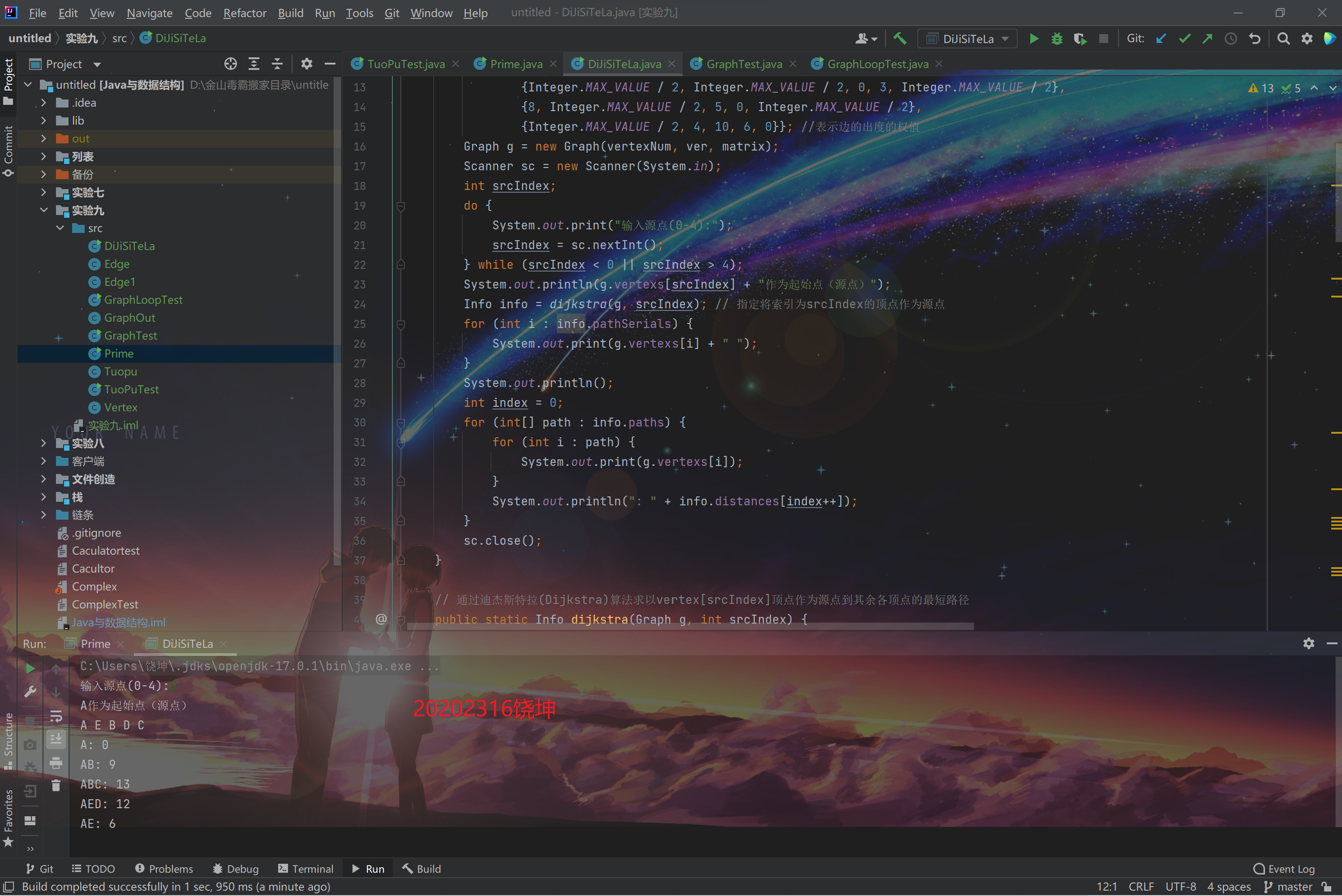
(5)完成有向图的单源最短路径求解(迪杰斯特拉算法)
- 通过Dijkstra计算图G中的最短路径时,需要指定一个起点D(即从顶点D开始计算)。
- 此外,引进两个数组S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点D的距离)。
- 初始时,数组S中只有起点D;数组U中是除起点D之外的顶点,并且数组U中记录各顶点到起点D的距离。如果顶点与起点D不相邻,距离为无穷大。
- 然后,从数组U中找出路径最短的顶点K,并将其加入到数组S中;同时,从数组U中移除顶点K。接着,更新数组U中的各顶点到起点D的距离。
- 重复第4步操作,直到遍历完所有顶点




## 3. 实验过程中遇到的问题和解决过程
- 问题1:在编写深度遍历算法的时候,遍历过程总是不对,与实际结果不符合
- 问题1解决方案:发现是我的栈用错了,后面我改了之后终于成功运行出来了
- 问题2:最小生成树的编写中,邻接矩阵总是出错
- 问题2解决方案:我用-1来表示无法到达的点,这下十分完美的输出结果。
## 其他
感悟:最后一次的实验了,总的来说这一学期的收获还是蛮多,超人的课我们都上的是十分的开心,也学到了蛮多的知识,虽说这一次的图的相关实验对于我来说还是难度十分的大,我看着着一个个算法脑袋真的是大的离谱了,我这水平真的菜的过分了,虽说以后就没有数据结构的课了,但是我应该会抽时间去练习Java的,对吧。
## 参考资料
- 《Java程序设计教程(第九版)》
- 《Java软件结构与数据结构(第四版)》
- 网页搜索资料:图的遍历:https://blog.csdn.net/qq_22238021/article/details/78286798
- Prim算法或Kruscal算法:https://www.cnblogs.com/yghjava/p/6858364.html
- 云班课:https://www.cnblogs.com/rocedu/p/6371262.html



