poj1200

原题：

 

 题目意思大致是这样 

输入的NC 如4 说明输入的这个addbabac 有abcd四个不同字符

输入的N 如 3 是指子串长度

输入的s 如daababac是主串

我们要找主串中不同的连续子串数目 子串长度必须为N

如daababac 有

 

 这五个不同连续子串

 

这样一看 好像这个NC没啥用 我们先用最简单的方法写一遍

#include<cstdio>
#include<iostream>
#include<set>
#include<string>

using namespace std;
int main()
{
    int N,NC;
    scanf("%d%d",&N,&NC);
    string q;
    cin>>q;
    set<string> c;
    for(int i =0; i < q.size()-N+1;i++)
    {
        c.insert(q.substr(i,N));
    }
    cout<<c.size()<<endl;
    return 0;
}

我们直接暴力遍历一遍 把所有遍历的放了去重容器set中 再直接数set多少个元素就行

果不其然超时了。这种看似简单的题基本都会卡输入输出

所以想想怎么优化：

具体思路是

首先cin cout肯定不能有 

string也避免用 

就用c写不去用stl

然后再想想优化算法

我们之前是直接暴力比较

set是红黑树 插入的时间复杂度是O（logN）但是里边还有一个string的substr 这个substr截取子串的话如果用char数组，char*去想想实现原理

平均应该也有个n/2次 那时间复杂度是o（N）

 

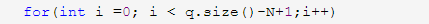
 上边还有一个循环

这个时间复杂度粗略估算是三个乘起来 怎么也得比o(n²）o（n*m）高

所以算法必须优化。之前这个算法好处就是 set这个红黑树的logn时间复杂度还挺好 所以要善于用set

怎么优化呢 用哈希

这样这个NC就用上了

举个例子

对于addbabac 这个串 我们用c的语言特点

a虽然是char 但是int值也是97

a-z这些字符他们的int值本身也是哈希值 一一映射

这就方便我们直接用int数组记录哈希

还有就是 这个NC提示我们要用NC进制去标识 这个s转化的唯一NC进制数

之后我们把字符 字符串的比较转化为了数字的比较 

举个例子 10进制 每位就是0-9 唯一标识了一个数 假如abcd是 1234

就不会有adbb也是1234 和他重复 

ac代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long int
const int maxn = 16000000 + 3;
char s[maxn];
int not_0[maxn];
int num[301];
int N,NC;
void hash(char *s)
{
    int len = strlen(s);
    int temp = 0;
    num[s[0]] = temp++;  
    for(int i=1;i<len;i++)
    { 
        if(num[s[i]] == 0)
            num[s[i]] = temp ++;
    } //num[s[i]] char -> int
}
int get_cnt(int l,int r)
{
    int sum = 0;
    for(int i=l;i<=r;i++)
    {
        sum = sum * NC + num[s[i]];
    }
    return sum;
}
int main()
{
    while(~scanf("%d%d%s",&N,&NC,s))
    {
        int ans = 0;
        int len = strlen(s);
        hash(s);
        for(int i=0;i<=len-N;i++)
        {
            int cnt = get_cnt(i, i+N-1);
            if(!not_0[cnt])
            {
                ans ++;
                not_0[cnt] = 666;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}