彻底理解RSA加密算法

RSA是非常典型的非对称加密算法

 

 

它的算法是这样的

 

加密是我们把明文M转化成密文C 需要用到加密运算 而解密时我们要用解密运算将密文C转化成M 从表达式中

可以看出 e和d使我们需要确定的参数 而N是两者共有的 所以我们把参数e，d称之为私钥 N就是公钥 两者都属于密钥 

这里M比N小 我们不能狭义地去看待这些数 因为计算机本质上传输的都是二进制数据 计算机是用电信号 所以所谓图片 影片 文本等等不都是二进制数据么 也就是数

看起来好像很简单 

但是我们现在面临几个问题 首先 初始时e怎么确定 N怎么确定 

其次 由e和N如何确定d的值 从而进行解密操作

还有 为什么解密这个式子是成立的 为什么可以这么解密

 

 我们先保存这些问题 来看一下RSA密钥的产生过程

首先 我们随机选择两个大素数p，q

计算N=pq

此时

 

上式的证明如下：

如果m和n是互质的正整数。那么，ϕ(mn)=ϕ(m)ϕ(n)=（m-1）（n-1）

 

 

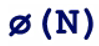是N的欧拉函数  

 

 

 之后

 

 

 gcd就是我们的欧几里得算法 c++代码如下

int gcd(int a,int b)///辗转相除法求最大公约数
{

    int t = a;
    while(a%b)
    {
        a=b;
        b=t%b;
        t=a;
    }
    return b;
}

这个还可以直接递归实现

int gcd(int a, int b)
{
    return b == 0 ? a : gcd(b, a%b);
}

 

也就是说 当gcd的两个参数互质时 函数值才是1 所以e与N的欧拉函数互质(欧几里得算法用来求最大公约数）

之后我们求解下列方程解出d

其实也就是ed mod φ(N)=1 解出d

 

 

 两个-是= 三个-是同余的意思 也就是说 ed mod φ(N)=1 mod  φ(N) = 1

最后我们再保存公钥和私钥 算法结束 

 

 

现在我们来讨论一下其中的问题

 

首先我们要知道欧拉定理：

在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则:

 

 

 也就是 a的φ(N)次方 对n取余 = 1

其证明如下：

 

 

 

 此时根据欧拉定理我们又可以又有一个推论：

 

 

 

 

 

 

 

 

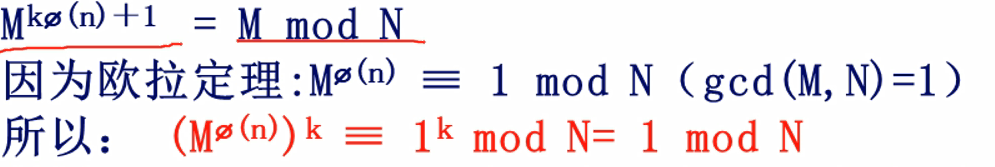
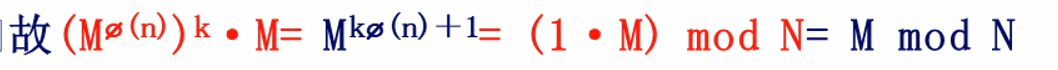
 我们可以用这些推论来解决实际问题

比如用来简化幂的模运算

问题如下：

计算7^{222}的个位数

实际是求7^{222}被10除的余数。7和10[[互素]]，且φ(10)=4

 

 

 

 

 

 

 

 

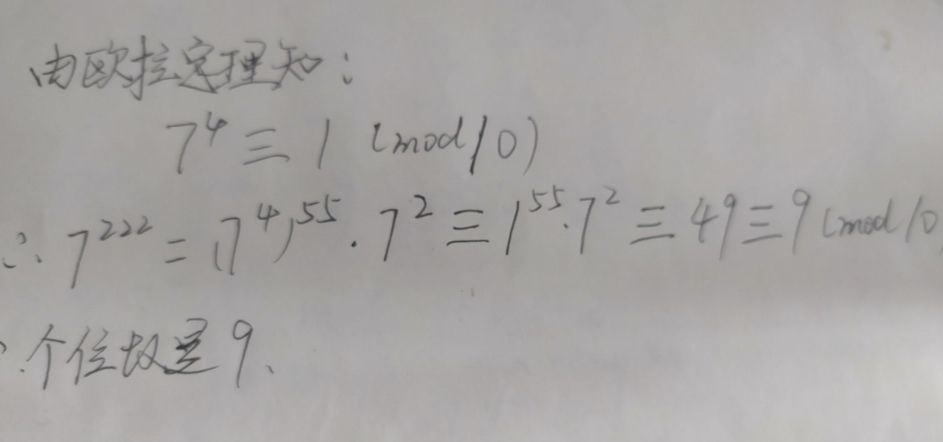
 现在 我们回到RSA算法中 我们选择e时 肯定是要小于φ（N） 之后我们要选择d 而使得ed mod φ（N）=1

那么因为我们合适的d值 就会存在 ed = 1+ kφ（N）

所以我们开始的解密和加密公式

C^d =(M^e)^d=M^(1+kφ（N) )=M mod N 得证

而如何去选择合适的d值

我们发现 ed mod φ(N) = 1

所以求d  就是求e对φ（N)的乘法逆元

 

求解乘法逆元 我们首先想到的是 简单暴力的迭代算法：

int d；
 for (d = 1;; d++) ///求d d是e的乘法逆元 n1是φ（N）
    {
        if (d * e % n1 == 1)
            break;
    }

但是这样又一个坏处 因为d是从1开始一直自增1去遍历 所以n1不能太大 也就是说p和q不能太大 但是本身p，q需要是大质数 这样才能保证加密的性能

于是我们

需要用到扩展欧几里得算法求乘法逆元d

 

要了解扩展欧几里得算法我们需要先知道贝祖定理：

若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。

它的一个重要推论是：a,b互质的充要条件是存在整数x,y使ax+by=1.

 

 

 所以 通常谈到最大公约数时，我们都会提到一个非常基本的事实：给予二个整数a、b，必存在整数x、y使得ax + by = gcd(a,b)。

 

有两个数a,b，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到ax+by=gcd(a,b)的整数解。

扩展欧几里得算法可以用来计算模反元素(也叫模逆元)，而模反元素在RSA加密算法中有举足轻重的地位。

 

我们举个例子：

用类似辗转相除法，求二元一次不定方程47x+30y=1的整数解

 

 这个过程也可以用矩阵表示 q表示商，r表示余数

 

 

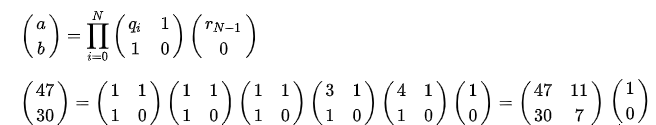
那么使用扩展欧几里德算法的过程应该是这样：

求exgcd(e, m)—>利用欧几里得算法不断递归直到x=1,y=0—>反向递归求出第一层的x和y，x即为e模m的逆元。

 

用代数表示一下 就是

我们要处理的是求出 a 和 b的最大公约数，并求出 x 和 y 使得 a*x + b*y= gcd ，而我们已经求出了下一个状态：b 和 a%b 的最大公约数，并且求出了一组x1 和y1 使得： b*x1 + (a%b)*y1 = gcd ， 这两个相邻的状态之间应该存在一种关系

那么我们来验证一下：

  我们给出这一条定理： a%b = a - (a/b)*b  //c系语言的除是取整数部分的除  因为欧拉定理我们清楚地知道 gcd（a,b）= gcd(b,a % b)

带入化简

 gcd = b*x1 + (a-(a/b)*b)*y1

            = b*x1 + a*y1 – (a/b)*b*y1

            = a*y1 + b*(x1 – a/b*y1)

 对比之前我们的状态：求一组 x 和 y 使得：a*x + b*y = gcd 

根据恒等定理 系数是不是要相同啊：

没错

x = y1

 y = x1 – a/b*y1

这时候 我们就可以写出扩展欧几里得算法

int exgcd(int a2,int  b2,int &x,int &y)
{
    if(b2==0)
    {
        x=1;y=0;
        return a2;
    }

    int ans = exgcd(b2,a2%b2,x,y);
    double temp=x;
    x=y;
    y=temp-a2/b2*y;
    return ans;       ///返回的还是最大公约数 但是我们就方便求x和y

}

这时候 我们很方便地可以求x和y  也就可以求出乘法逆元

乘法逆元是： ed mod φ（N）=1

也就存在这个表达式 ed +kφ（N）= 1 根据前边我们知道当gcd(ed φ（N）) != 1 的时候是没有解

一般，根据不定方程等数论部分的知识 我们应该能够找到无数组解满足条件，但是谁会闲的无聊让你写一堆通解

一般是让你求解出最小的那组解，怎么做？我们求解出来了一个特殊的解 x0 那么，我们用 x0 %  φ（N）其实就得到了最小的解了

因为啊 d的通解正是x0+kt

 也就是说  d对于 φ（N） 的逆元是一个关于 φ（N） 同余的

那么根据最小整数原理，一定存在一个最小的正整数，它是 d 关于φ（N） 的逆元，而最小的肯定是在（0 , φ（N））之间的，而且只有一个 这些都是纯数学推导

不得不说数学真的很重要

这时候还有一点要注意 我们有时候得到的x0可能是负数 所以要用函数abs（）取绝对值

至此 所有RSA加密的问题都迎刃而解了

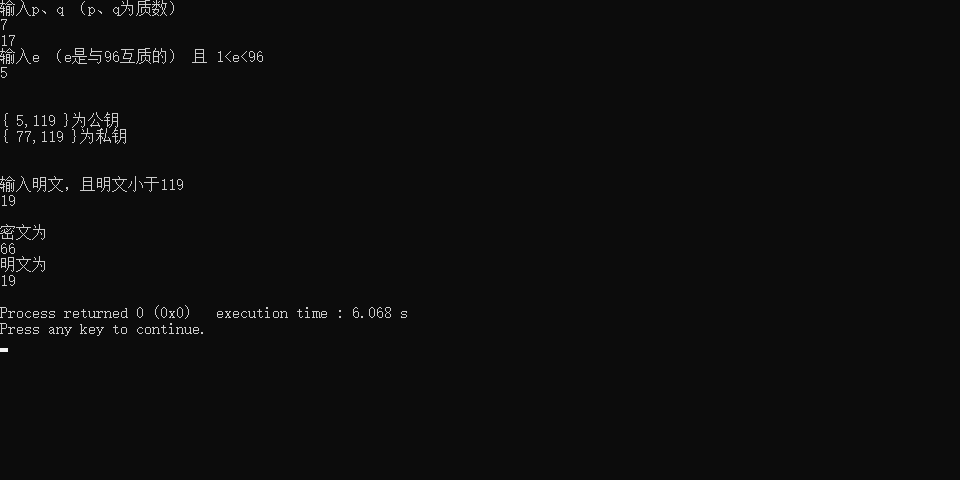
现在我给出模拟RSA加密的总代码

#include<bits/stdc++.h>
using namespace std;
int gcd(int a,int b)///辗转相除法求最大公约数
{

    int t = a;
    while(a%b!=0)
    {
        a=b;
        b=t%b;
        t=a;
    }
    return b;
}

int x,y,q;
int exgcd(int a2,int  b2,int &x,int &y)
{
    if(b2==0)
    {
        x=1;y=0;
        return a2;
    }

    int ans = exgcd(b2,a2%b2,x,y);
    double temp=x;
    x=y;
    y=temp-a2/b2*y;
    return ans;       ///返回的还是最大公约数 但是我们就方便求x和y

}
int tocal(int a3,int b3)
{
    int x0,y0;
    int gcd = exgcd(a3,b3,x0,y0);
    if(1%gcd!=0) return -1; ///gcd得等于1  ...
    x0*=1/gcd;
    b3=abs(b3);
    int ans = x0%b3;
    if (ans<=0) ans+=b3;
    return ans;


}
int main()
{
    int p, q;
    cout << "输入p、q （p、q为质数）" << endl;
    cin >> p >> q;
    int n = p * q;
    int n1 = (p - 1) * (q - 1);///欧几里得函数
    int e;
    cout << "输入e （e是与" << n1 << "互质的） 且 1<e<" << n1 << endl;///按照定义来
    cin >> e;
    int d;
    /*其实也可以穷举法求d 但是这样 输入的p和q不能过大 所以n1才不会太大
    for (d = 1;; d++) ///求d d是e的乘法逆元
    {
        if (d * e % n1 == 1)
            break;
    }
    */
    d = tocal(e,n1);

    cout << endl << endl;

    cout << "{ " << e << "," << n << " }" << "为公钥" << endl;
    cout << "{ " << d << "," << n << " }" << "为私钥" << endl;


    cout << endl << endl;

    int before;
    cout << "输入明文，且明文小于"<<n << endl;
    cin >> before;

    cout << endl;
    int i;

    cout << "密文为" << endl;
    int after;
    after = before % n;
    for (i = 1; i < e; i++)
    {
        after = (after * before) % n;
    }
    cout << after << endl;

    cout << "明文为" << endl;
    int real;
    real = after % n;
    for (i = 1; i < d; i++)
    {
        real = (real * after) % n;
    }
    cout << real << endl;
    return 0;

}

 

运行结果：完全正确

 

 

 

 后话：最初的网络安全都是基于对称加密。没有公钥私钥之分 一旦别人拥有密钥 数据就会泄露；

后来地球上出现了迄今为止最重要的非对称加密RSA算法。

公钥对外公开 而私钥自己保有

世界上很多事情，都是单向（或者反向问题难度大大增加）的。杀一个人比救一个人容易 摔碎一个餐具比拼好一个餐具容易 研究毒药比研究毒药的解药容易

令两个大素数相乘容易 把一个大数分解成两个素数相乘就很难

解密确实用了私钥，一个跟加密过程不一致的方式。即解密并不是我们常识理解的那种逆运算，比如1+1=2，反过来2-1=1。但是RSA却不是这样很显然的方式

所以才叫非对称加密 这样对概念也就能深深的理解