对循环神经网络参数的理解|LSTM RNN Input_size Batch Sequence

在很多博客和知乎中我看到了许多对于pytorch框架中RNN接口的一些解析，但都较为浅显甚至出现一些不准确的理解，在这里我想阐述下我对于pytorch中RNN接口的参数的理解。

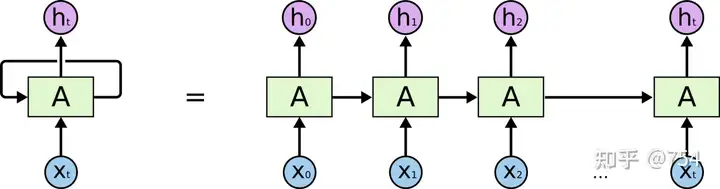
我们经常看到的RNN网络是如图下所示：

RNN的

1. timestep训练过程

这个左边图中间循环的箭头难以理解，所以将其按照时间轴展开成多个单元。

但是！！！！

网络只有一个，网络只有一个,网络只有一个， 并不是想右边那样画的。右边的图只不过是不同时刻的输入。因为每个时刻RNN会产生两个输出，一个output和一个state（state是输入向下一个时序的结果），上一个时刻state和当前作为输入给当前网络，就如右图所示。上图很容易造成了误解。

比如我们需要预测一个sin函数，那么我们会用x的坐标去预测y，batchsize=1(batch_size的问题较为复杂，后续会聊)，timestep(sequence的长度)为5，特征为1(只有x坐标)，所以整个训练过程是这样的，我们预备出5个坐标，一个一个依次放入到网络中，初始化的h0是0，然后会得到h1，去得到h2，用h2和x3去得到h4，以此类推。。。我们其实只要看上图的左边，不要被右图给搞混，只有一个网络结构而已。只是不停的放入不停的迭代。

2. batch理解

网上对batch的理解鱼龙混杂，什么样的解释都有，这里我要阐述我的观点，用一个博客上的例子，

给定一个长序列，序列中的每一个值，也都由一个很长的向量（或矩阵）表示。把序列从前往后理解为时间维度，那么timestep就是指的这个维度中的值，如果timestep=n，就是用序列内的n个向量（或矩阵）预测一个值,下图的timestep为2。

而对于每一个向量来说，它本身有一个空间维度（如长度），那么Batchsize就是这个空间维度上的概念。

比如一共有5个字母ABCDE，它们分别如此表示：

A：1 1 1 1 1

B：2 2 2 2 2

C：3 3 3 3 3

D：4 4 4 4 4

E：5 5 5 5 5

X	Y
AB	C
BC	D
CD	E

下面我们只看第一对数据：AB-C

t=0,A进入训练，生成h(0)

t=1,B进入训练，生成h(1)

如果我们分batch的话，设batch=2，那就AB-C, BC-D一起放入训练，同时平均loss之后经过一次backward更新超参数，由于超参数的方法更新很多，可能是类似于加权的平均。

这样或许很抽象，于是我我以文本数据为例画了一张图

3. hidden_size理解

hidden_size类似于全连接网络的结点个数，hidden_size的维度等于hn的维度，这就是每个时间输出的维度结果。我们的hidden_size是自己定的，根据炼丹得到最佳结果。

为什么我们的input_size可以和hidden_size不同呢，因为超参数已经帮我们完成了升维或降维，如下图(超参数计算流程)。

此时我引用正弦预测例子，后续会展示代码，其中input_size=1,hidden_size=50。

我们可以得到以下结果：

代码附下:

import numpy as np
import pandas as pd

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# %matplotlib inline

# 跟matlab差不多 返回一个1维张量，包含在区间start和end上均匀间隔的step个点。
# torch.linspace(start, end, steps, out=None) → Tensor
x = torch.linspace(0,799,800)

y = torch.sin(x*2*3.1416/40)

plt.figure(figsize=(12,4))
plt.xlim(-10,801)
plt.grid(True)
plt.xlabel("x")
plt.ylabel("sin")
plt.title("Sin plot")
plt.plot(y.numpy(),color='#8000ff')
plt.show()

test_size = 40
train_set = y[:-test_size]#前760个数
test_set = y[-test_size:]#后40个数


plt.figure(figsize=(12,4))
plt.xlim(-10,801)
plt.grid(True)
plt.xlabel("x")
plt.ylabel("sin")
plt.title("Sin plot")
plt.plot(train_set.numpy(),color='#8000ff')
plt.plot(range(760,800),test_set.numpy(),color="#ff8000")
plt.show()

# 在使用LSTM模型时，我们将训练序列分为一系列重叠的窗口。用于比较的标签是序列中的下一个值。【滑动窗口】
# 例如，如果我们有一系列12条记录，窗口大小为3，我们将[x1, x2, x3]送入模型，并将预测值与x4比较。
# 然后我们回溯，更新参数，将[x2, x3, x4]输入模型，并将预测结果与x5进行比较。
# 为了简化这个过程，我定义了一个函数input_data(seq,ws)，创建了一个(seq,labels)图元的列表。
# 如果ws是窗口大小，那么（seq,labels）图元的总数将是len(series)-ws。

def input_data(seq, ws):
    out = []
    L = len(seq)

    for i in range(L - ws):
        window = seq[i:i + ws]
        label = seq[i + ws:i + ws + 1]
        out.append((window, label))

    return out

# The length of x = 800
# The length of train_set = 800 - 40 = 760
# The length of train_data = 760 - 40 - 720

window_size = 40
train_data = input_data(train_set, window_size)
len(train_data)

train_data[0]#40个滑动窗口，作为一个输入


class LSTM(nn.Module):
    def __init__(self, input_size=1, hidden_size=50, out_size=1):
        super().__init__()
        self.hidden_size = hidden_size
        self.lstm = nn.LSTM(input_size, hidden_size)
        self.linear = nn.Linear(hidden_size, out_size)
        self.hidden = (torch.zeros(1, 1, hidden_size), torch.zeros(1, 1, hidden_size))

    def forward(self, seq):
        lstm_out, self.hidden = self.lstm(seq.view(len(seq), 1, -1), self.hidden)
        pred = self.linear(lstm_out.view(len(seq), -1))
        return pred[-1]

torch.manual_seed(42)
model = LSTM()
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

epochs = 10
future = 40

for i in range(epochs):

    for seq, y_train in train_data:
        optimizer.zero_grad()
        model.hidden = (torch.zeros(1, 1, model.hidden_size),
                        torch.zeros(1, 1, model.hidden_size))

        y_pred = model(seq)
        loss = criterion(y_pred, y_train)
        loss.backward()
        optimizer.step()

    print(f"Epoch {i} Loss: {loss.item()}")

    preds = train_set[-window_size:].tolist()
    for f in range(future):
        seq = torch.FloatTensor(preds[-window_size:])
        with torch.no_grad():
            model.hidden = (torch.zeros(1, 1, model.hidden_size),
                            torch.zeros(1, 1, model.hidden_size))
            preds.append(model(seq).item())

    loss = criterion(torch.tensor(preds[-window_size:]), y[760:])
    print(f"Performance on test range: {loss}")

    plt.figure(figsize=(12, 4))
    plt.xlim(700, 801)
    plt.grid(True)
    plt.plot(y.numpy(), color='#8000ff')
    plt.plot(range(760, 800), preds[window_size:], color='#ff8000')
    plt.show()

参考文章：https://zhuanlan.zhihu.com/p/460282865
原创作者：孤飞-博客园
个人博客：https://blog.onefly.top