[BZOJ2616][SPOJ PERIODNI] Periodni (树形背包)
简易题意
有$n$个$1 \times h_i$的空地，顺次拼成一个大的空地，其中不是空地的地方就是墙。现在要求在空地上放车，要求车不能互相攻击到。
数据范围
$n,m\leq500\ h_i\leq1000000$
题解
这题第一感觉是个暴力hash+DP，使用组合数进行转移。
首先先想按列考虑，但是按列考虑空地的高度有可能增长也有可能降低，因此不方便进行转移。
换个思路，我们可以按行考虑。
如果每次从高往低扫，每次截取当前这条线以上的空地图形，与之前相比，会产生新的联通块或者合并旧的联通块。
合并旧的联通块当且仅当这个位置的高度是之前两个旧的联通块内最小的之。
我们可以反方向考虑，从合并联通块变成分裂联通块。
每次分裂的时候，找到这一段内最小的值，之后将其分裂。
对于每一段，我们定义$dp_{j}$表示在当前联通块（段）放$j$个车时的方案数。
容易看出，每次转移的时候，新联通块一定是一堆旧的联通块加上一个矩形
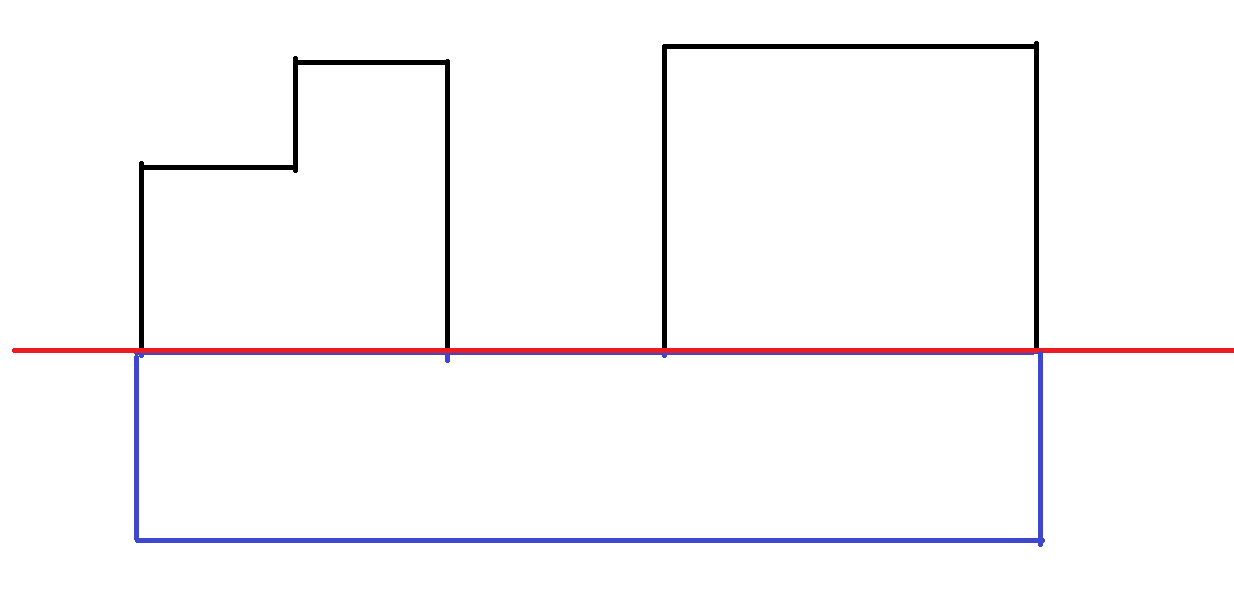
对于新的联通块，我们并不在意上面几个联通块哪些位置放了车，只在意有几列被放了车，即放了几个车。
因此，我们合并的时候先统计旧的联通块有多少种合法情况放了$i$个车，这很明显是一个使用背包的计数题。
处理完上面的联通块后，我们再处理下面新增的矩形。
我们只需要枚举上面联通块车的个数，和下面联通块车的个数，就可以利用组合数算出情况个数。
$$
dp_{i+j}=\sum dp_i\times C_{\Delta h}^j \times A_{len}^j
$$
（似乎$dp_0$要特殊处理）
答案就是总段的$dp_k$
代码
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#include<bitset>
using namespace std;
template<typename __T>
inline void read(__T &x)
{
x=0;
int f=1;char c=getchar();
while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
while(isdigit(c)) {x=x*10+c-'0';c=getchar();}
x*=f;
}
const int mod=1000000007;
int frac[1000005];
int fracinv[1000005];
long long qpow(long long a,long long b)
{
long long ans=1;
while(b)
{
if(b&1) ans=(ans*a)%mod;
b>>=1;
a=a*a%mod;
}
return ans;
}
int C(int n,int m)
{
if(n<m) return 0;
return 1ll*frac[n]*fracinv[n-m]%mod*fracinv[m]%mod;
}
int Cinv(int n,int m)
{
return 1ll*fracinv[n]*frac[n-m]%mod*frac[m]%mod;
}
int A(int n,int m)
{
return 1ll*frac[n]*fracinv[n-m]%mod;
}
int h[505];
int n,k;
int dp[505][505];
int tmp[505];
int tot=1;
void dfs(int l,int r,int id,int lasth)
{
int minz=12345678;
for(int i=l;i<=r;i++)
minz=min(minz,h[i]);
int top=0;
int sta[505];
for(int i=l;i<=r;i++)
if(h[i]==minz)
sta[top++]=i;
if(top==r-l+1)
{
for(int i=0;i<=top;i++)
dp[id][i]=1ll*C(minz-lasth,i)*A(top,i)%mod;
return;
}
int laspos=l;
int edpos=l;
dp[id][0]=1;
while(laspos<=r)
{
while(h[laspos]==minz) laspos++;
if(laspos>r) break;
edpos=laspos;
while(edpos<r && h[edpos+1]>minz) edpos++;
int neid=++tot;
dfs(laspos,edpos,neid,minz);
memcpy(tmp,dp[id],4*k+4);
memset(dp[id],0,4*k+4);
for(int i=0;i<=laspos;i++)
for(int j=0;j<=edpos-laspos+1;j++)
dp[id][i+j]=(dp[id][i+j]+1ll*tmp[i]*dp[neid][j])%mod;
dp[id][0]=1;
laspos=edpos+1;
}
memcpy(tmp,dp[id],4*k+4);
memset(dp[id],0,4*k+4);
for(int i=0;i<=r-l+1-top;i++)
for(int j=0;j<=r-l+1-i;j++)
dp[id][i+j]=(dp[id][i+j]+1ll*tmp[i]*C(minz-lasth,j)%mod*A(r-l+1-i,j))%mod;
dp[id][0]=1;
}
int main()
{
read(n);
read(k);
int sbsx=n;
for(int i=0;i<n;i++)
{
read(h[i]);
sbsx=max(sbsx,h[i]);
}
frac[0]=1;
for(int i=1;i<=sbsx;i++)
frac[i]=1ll*frac[i-1]*i%mod;
fracinv[sbsx]=qpow(frac[sbsx],mod-2);
for(int i=sbsx-1;i>0;i--)
fracinv[i]=1ll*fracinv[i+1]*(i+1)%mod;
fracinv[0]=1;
dfs(0,n-1,1,0);
printf("%d\n",dp[1][k]);
return 0;
}
参考
没有
