GCN学习笔记
很好的翻译:http://www.elecfans.com/rengongzhineng/603772.html 才发现自己翻译的太渣了,还花了很长时间,呜呜~全当练习英语了

In the last couple of years, a number of papers re-visited this problem of generalizing neural networks to work on arbitrarily structured graphs (结构化图)
(Bruna et al., ICLR 2014; Henaff et al., 2015; Duvenaud et al., NIPS 2015; Li et al., ICLR 2016; Defferrard et al., NIPS 2016; Kipf & Welling, ICLR 2017),
some of them now achieving very promising results in domains that have previously been dominated by, e.g., kernel-based methods, graph-based regularization techniques and others.
Outline
- Short introduction to neural network models on graphs
- Spectral graph convolutions and Graph Convolutional Networks (GCNs)
- Demo: Graph embeddings with a simple 1st-order GCN model 使用简单的一阶GCN模型进行图形嵌入
- GCNs as differentiable generalization of the Weisfeiler-Lehman algorithm GCN是Weisfeiler-Lehman算法的可微分推广
If you're already familiar with GCNs and related methods, you might want to jump directly to Embedding the karate club network.
Recent literature相关文献
Some recent papers introduce problem-specific specialized architectures (e.g. Duvenaud et al., NIPS 2015; Li et al., ICLR 2016; Jain et al., CVPR 2016),
others make use of graph convolutions known from spectral graph theory1 (Bruna et al., ICLR 2014; Henaff et al., 2015) to define parameterized filters(参数滤波器) that are used in a multi-layer neural network model多层神经网络模型,类似于我们所知道和喜爱的“经典”CNN。
More recent work focuses on bridging the gap between fast heuristics and the slow2,更原则性的谱方法。Defferrard et al. (NIPS 2016) approximate smooth filters in the spectral domain using Chebyshev shpolynomials with free parameters that are learned in a neural network-like model. They achieve convincing results on regular domains (like MNIST), closely approaching those of a simple 2D CNN model.Defferrard等人。 (NIPS 2016)使用Chebyshev shpolynomials切比雪夫多项式在谱域中*似*滑滤波器,其中自由参数是在神经网络模型中学习的。它们在常规域(如MNIST)上取得令人信服的结果,与简单的2D CNN模型非常接*。
In Kipf & Welling (ICLR 2017)采用了一种类似的方法,从光谱图卷积的框架开始,yet introduce simplifications (we will get to those later in the post) that in many cases allow both for significantly faster training times and higher predictive accuracy, reaching state-of-the-art classification results on a number of benchmark graph datasets.然后引入简化(我们将在后面的文章中介绍),在许多情况下允许两者显着加快训练时间 更高的预测准确性,在许多基准图数据集上达到最先进的分类结果。
一般化CNN、RNN这样的神经网络并且将它们应用在图结构数据上是一个很有挑战性的工作。最*有一些论文提出了针对特定问题的专用架构(比如,Duvenaud等, NIPS 2015; Li et等, ICLR 2016; Jain等, CVPR 2016),还有一些论文运用基于谱图理论的图卷积来定义参数化的滤波器(filter)(Bruna等, ICLR 2014; Henaff等, 2015),并将它们应用在我们熟知的经典多层CNN网络中。
另外最*更多的工作重点是结合速度快的启发式算法和速度慢但更合理的谱方法。Defferrard等人 (NIPS 2016)使用带有自由参数的Chebyshev多项式在谱域中*似得到*滑的滤波器,其中参数可以通过一个类似神经网络的模型学习。他们在常用的数据集(MNIST)得到了令人信服的结果,和简单的2维CNN模型的结果非常接*。
在这篇(Kipf & Welling等,ICLR 2017)文章中,我们使用了一个相似的方法并且也是从谱图卷积的框架出发,并引入了一种简化方式(稍后介绍)既能明显加快训练时间又能得到更高的预测精度,在一些基准的图数据集上,达到了最好的效果。
GCNs Part I: Definitions
目前,大多数图形神经网络模型具有一些共同的通用架构。 我将这些模型称为图形卷积网络(GCN); 卷积,因为滤波器参数通常在图中的所有位置(或其子集,如 in Duvenaud et al., NIPS 2015)共享。
对于这些模型,目标是学习图G=(V,E)(V顶点 E边)上的信号/特征函数,该函数作为输入:
1.每个节点i的特征描述为xi;用N×D维特征矩阵X概括(N:节点数,D:输入特征数)
2.矩阵形式的图结构的代表性描述,通常以邻接矩阵A(或其某些功能)的形式( aij=0为不相邻,aij=1为相邻)
并产生一个节点级输出Z(N×F维特征矩阵),其中F是每个节点的输出特征数)。 图形级输出可以通过引入某种形式的池化操作来建模(参见,e.g. Duvenaud et al., NIPS 2015)。
然后可以将每个神经网络层写为非线性函数
![]()
![]() (或图表级输出的z),L是层数。 然后,具体模型的区别仅在于如何选择 f(⋅,⋅)和参数化。
(或图表级输出的z),L是层数。 然后,具体模型的区别仅在于如何选择 f(⋅,⋅)和参数化。
GCNs Part II: A simple example
作为一个例子,让我们考虑以下非常简单的分层传播规则形式:
![]()
W(l)是第l个神经网络层的权重矩阵,σ(⋅)是一个像ReLU一样的非线性激活函数。尽管它很简单,但这个模型已经非常强大(我们马上就会谈到它)。
但首先,让我们解决这个简单模型的两个局限性:
1.与 A 相乘意味着,对每个节点都是将所有相邻节点的特征向量的加和而不包括节点本身(除非图中存在自循环)。我们可以通过在图中强制执行自我循环来「解决」这个问题——只需要将恒等矩阵添加到 A 上。
2.第二个局限性主要是 A 通常不是归一化的,因此与 A 相乘将完全改变特征向量的分布范围(我们可以通过查看 A 的特征值来理解)。归一化 A 使得所有行总和为 1,即 D^-1 A,其中 D 是对角节点度矩阵,这样即可避免这个问题。归一化后,乘以 D^-1 A 相当于取相邻节点特征的*均值。在实际应用中可使用对称归一化,如 D^-1/2 A D^-1/2(不仅仅是相邻节点的*均),模型动态会变得更有趣。结合这两个技巧,我们基本上获得了Kipf & Welling (ICLR 2017)文章中介绍的传播规则:
结合这两个技巧,我们基本上得出了在Kipf & Welling (ICLR 2017)中引入的传播规则:

式中 A =A+I,I 是单位矩阵,D 是 A 的对角节点度矩阵。
在下一节中,我们将仔细研究这种类型的模型如何在一个非常简单的示例图上运行:Zachary's karate club network Zachary的空手道俱乐部网络(make sure to check out the Wikipedia article!))。
GCNs Part III: Embedding the karate club network 嵌入空手道俱乐部网络
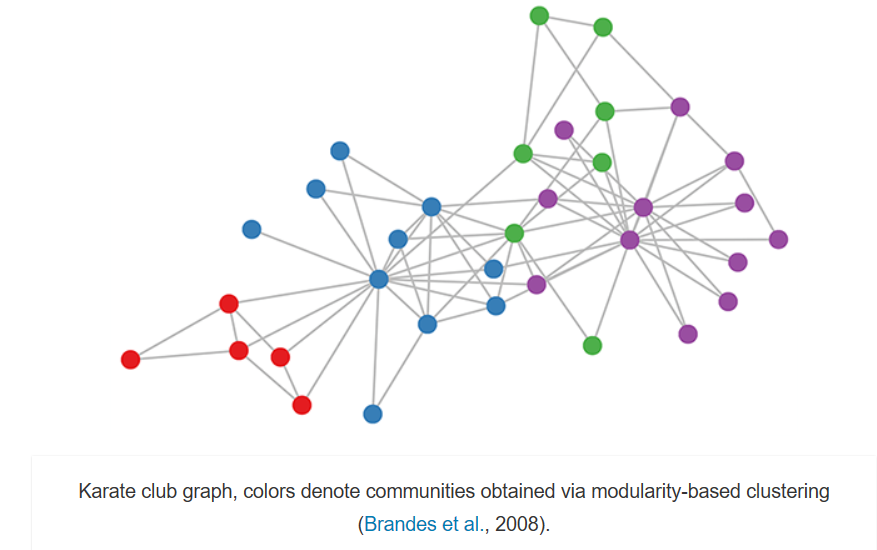
空手道俱乐部图表,颜色表示通过基于模块化的聚类获得的 communities社区(Brandes et al., 2008).
让我们来看看我们的简单GCN模型(参见上一节或Kipf & Welling, ICLR 2017)如何在著名的图形数据集上工作:Zachary的空手道俱乐部网络(见上图)。
Zachary空手道俱乐部是一个小型的社交网络,在这里,俱乐部管理员和教练之间会发生冲突。任务是预测,当冲突发生时,俱乐部成员会站在哪一边。俱乐部社交网络图表示如下:
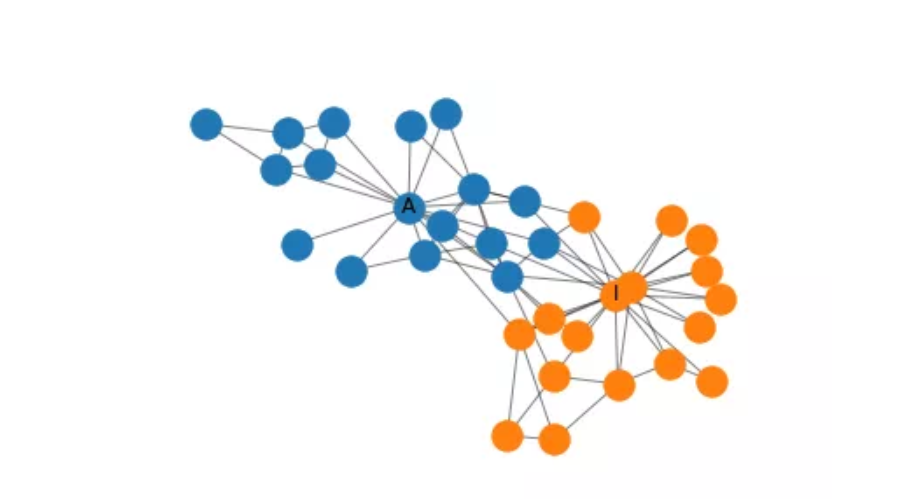
每个节点表示俱乐部的每个成员,成员之间的连接表示他们在俱乐部外进行的交互。管理员用是节点A,教练是节点I。
我们采用随机初始化权重的3层GCN。 现在,在训练权重之前,我们只需将图的adjacency matrix邻接矩阵A和X = I(即单位矩阵,因为我们没有任何节点特征)插入到模型中。 3层GCN现在前向传播期间执行三个传播步骤,并有效地卷积每个节点(图的节点)的3阶邻域(所有节点最多3“跳”)。值得注意的是,该模型为这些节点生成了一个与图的共同体结构非常相似的嵌入(见下图)。到目前为止,我们已经完全随机地初始化了权重,并且还没有做任何训练。

用于空手道俱乐部网络中节点的GCN嵌入(随机权重)。
这似乎有点令人惊讶。最*一篇名为 DeepWalk 的模型((Perozzi et al., KDD 2014))表明,他们可以在复杂的无监督训练过程中得到相似的嵌入。那我们怎么可能仅仅使用未经训练的简单 GCN 模型,就得到
这样的嵌入呢?
我们可以通过将 GCN 模型视为图论中著名的 Weisfeiler-Lehman 算法的广义可微版本,并从中得到一些启发。Weisfeiler-Lehman 算法是一维的,其工作原理如下 :
对所有的节点 vi∈G 求解邻*节点 {vj} 的特征 {hvj}
通过 hvi←hash(Σj hvj) 更新节点特征,该式中 hash(理想情况下)是一个单射散列函数
重复 k 步或直到函数收敛。
在实际应用中,Weisfeiler-Lehman 算法可以为大多数图赋予一组独特的特征。这意味着每个节点都被分配了一个独一无二的特征,该特征描述了该节点在图中的作用。但这对于像网格、链等高度规则的图是不适用的。对大多数不规则的图而言,特征分配可用于检查图的同构(即从节点排列,看两个图是否相同)。
回到我们图卷积的层传播规则(以向量形式表示):
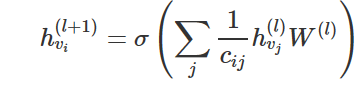
式中,j 表示 vi 的相邻节点。cij 是使用我们的 GCN 模型中的对称归一化邻接矩阵 D-1/2 A D-1/2 生成的边 (v_i,v_j) 的归一化常数。
我们可以将该传播规则解释为在原始的 Weisfeiler-Lehman 算法中使用的 hash 函数的可微和参数化(对 W(l))变体。如果我们现在选择一个适当的、非线性的的矩阵,并且初始化其随机权重,使它是正交的,(或者使用 Glorot & Bengio, AISTATS 2010 提出的初始化)那么这个更新规则在实际应用中会变得稳定(这也归功于归一化中的 c_ij 的使用)。我们得出了很有见地的结论,即我们得到了一个很有意义的*滑嵌入,其中可以用距离远*表示局部图结构的相似性/不相似性!
GCNs Part IV: Semi-supervised learning 半监督学习
由于我们模型中的所有内容都是可微分且参数化的,因此可以添加一些标签,使用这些标签训练模型并观察嵌入如何反应。我们可以使用Kipf & Welling (ICLR 2017).文章中介绍的 GCN 的半监督学习算法。我们只需对每类/共同体(下面视频中突出显示的节点)的一个节点进行标记,然后开始进行几次迭代训练:
用 GCNs 进行半监督分类:对每类仅仅标记一个标签,(突出显示标记节点)进行 300 次迭代训练得到隐空间的动态。

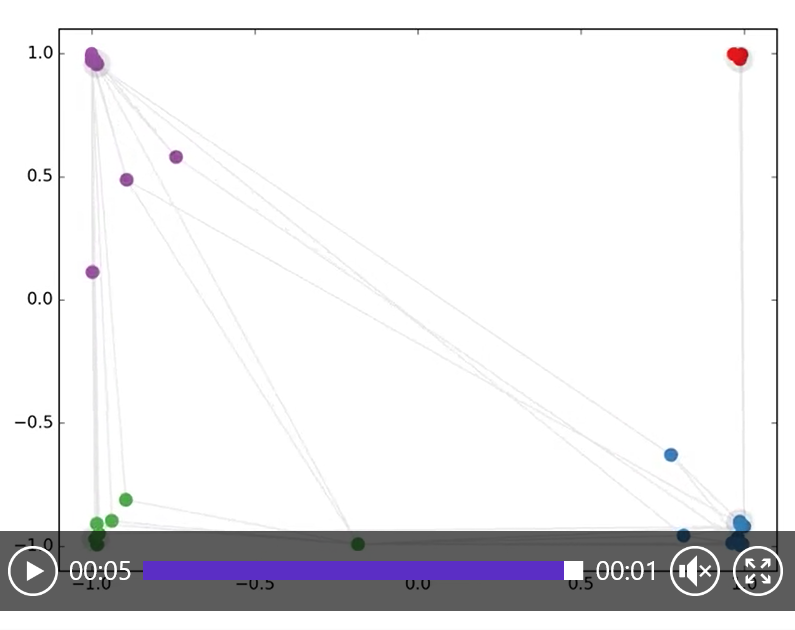
使用GCN进行半监督分类:潜在的空间动态,300次训练迭代,每类有一个标签。 被标记的节点突出显示。
请注意,该模型会直接生成一个二维的即时可视化的隐空间。我们观察到,三层 GCN 模型试图线性分离这些(只有一个标签实例的)类。这一结果是引人注目的,因为模型并没有接收节点的任何特征描述。与此同时,模型还可以提供初始的节点特征,因此在大量数据集上都可以得到当前最佳的分类结果,而这也正是我们在文章中描述的实验所得到的结果。
结论
有关这个领域的研究才刚刚起步。在过去的几个月中,该领域已经获得了振奋人心的发展,但是迄今为止,我们可能只是抓住了这些模型的表象。而神经网络如何在图论上针对特定类型的问题进行研究,如在定向图或关系图上进行学习,以及如何使用学习的图嵌入来完成下一步的任务等问题,还有待进一步探索。本文涉及的内容绝非详尽无遗的,而我希望在不久的将来会有更多有趣的应用和扩展。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号