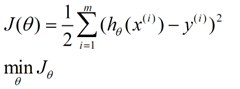逻辑回归模型(Logistic Regression, LR)--分类
逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,使得逻辑回归模型成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。本文主要详述逻辑回归模型的基础,至于逻辑回归模型的优化、逻辑回归与计算广告学等,请关注后续文章。
1 逻辑回归模型
回归是一种极易理解的模型,就相当于y=f(x),表明自变量x与因变量y的关系。最常见问题有如医生治病时的望、闻、问、切,之后判定病人是否生病或生了什么病,其中的望闻问切就是获取自变量x,即特征数据,判断是否生病就相当于获取因变量y,即预测分类。
最简单的回归是线性回归,在此借用Andrew NG的讲义,有如图1.a所示,X为数据点——肿瘤的大小,Y为观测值——是否是恶性肿瘤。通过构建线性回归模型,如hθ (x)所示,构建线性回归模型后,即可以根据肿瘤大小,预测是否为恶性肿瘤h θ (x)≥.05为恶性,h θ (x)<0.5为良性。

然而线性回归的鲁棒性很差,例如在图1.b的数据集上建立回归,因最右边噪点的存在,使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致,而分类范围,需要在[0,1]。逻辑回归就是一种减小预测范围,将预测值限定为[0,1]间的一种回归模型,其回归方程与回归曲线如图2所示。逻辑曲线在z=0时,十分敏感,在z>>0或z<<0处,都不敏感,将预测值限定为(0,1)。
 图2 逻辑方程与逻辑曲线
图2 逻辑方程与逻辑曲线
逻辑回归其实仅为在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,逻辑回归成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。对于多元逻辑回归,可用如下公式似合分类,其中公式(4)的变换,将在逻辑回归模型参数估计时,化简公式带来很多益处,y={0,1}为分类结果。 
对于训练数据集,特征数据x={x 1 , x 2 , … , x m }和对应的分类数据y={y 1 , y 2 , … , y m }。构建逻辑回归模型f(θ),最典型的构建方法便是应用极大似然估计。首先,对于单个样本,其后验概率为:
 那么,极大似然函数为:
那么,极大似然函数为:
 log似然是:
log似然是:

2 梯度下降
由第1节可知,求逻辑回归模型f(θ),等价于:
![]() 采用梯度下降法:
采用梯度下降法:
 从而迭代θ至收敛即可:
从而迭代θ至收敛即可:
![]()
3 模型评估
对于LR分类模型的评估,常用AUC来评估,关于AUC的更多定义与介绍,可见参考文献2,在此只介绍一种极简单的计算与理解方法。
 对于训练集的分类,训练方法1和训练方法2分类正确率都为80%,但明显可以感觉到训练方法1要比训练方法2好。因为训练方法1中,5和6两数据分类错误,但这两个数据位于分类面附近,而训练方法2中,将10和1两个数据分类错误,但这两个数据均离分类面较远。
对于训练集的分类,训练方法1和训练方法2分类正确率都为80%,但明显可以感觉到训练方法1要比训练方法2好。因为训练方法1中,5和6两数据分类错误,但这两个数据位于分类面附近,而训练方法2中,将10和1两个数据分类错误,但这两个数据均离分类面较远。
AUC正是衡量分类正确度的方法,将训练集中的label看两类{0,1}的分类问题,分类目标是将预测结果尽量将两者分开。将每个0和1看成一个pair关系,团中的训练集共有5*5=25个pair关系,只有将所有pair关系一至时,分类结果才是最好的,而auc为1。在训练方法1中,与10相关的pair关系完全正确,同样9、8、7的pair关系也完全正确,但对于6,其pair关系(6,5)关系错误,而与4、3、2、1的关系正确,故其auc为(25-1)/25=0.96;对于分类方法2,其6、7、8、9的pair关系,均有一个错误,即(6,1)、(7,1)、(8,1)、(9,1),对于数据点10,其正任何数据点的pair关系,都错误,即(10,1)、(10,2)、(10,3)、(10,4)、(10,5),故方法2的auc为(25-4-5)/25=0.64,因而正如直观所见,分类方法1要优于分类方法2。
回归问题的条件/前提:
1) 收集的数据
2) 假设的模型,即一个函数,这个函数里含有未知的参数,通过学习,可以估计出参数。然后利用这个模型去预测/分类新的数据。
# coding: utf-8 ''' Created on Oct 27, 2010 Logistic Regression Working Module @author: Peter ''' from numpy import * def loadDataSet(): dataMat = []; labelMat = [] fr = open('testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # three feature labelMat.append(int(lineArr[2])) return dataMat,labelMat def sigmoid(inX): return 1.0/(1+exp(-inX)) def gradAscent(dataMatIn, classLabels): dataMatrix = mat(dataMatIn) #convert to NumPy matrix labelMat = mat(classLabels).transpose() #convert to NumPy matrix # 行向量转化为列向量,转置 m,n = shape(dataMatrix) alpha = 0.001 maxCycles = 500 weights = ones((n,1)) for k in range(maxCycles): #heavy on matrix operations h = sigmoid(dataMatrix*weights) #matrix mult error = (labelMat - h) #vector subtraction weights = weights + alpha * dataMatrix.transpose()* error #matrix mult ##中间过程略:∂J(w)/∂w=1/2∂w(∑(hw(x)−y)2)=(hw(x)−y)x(i) return weights def stocGradAscent0(dataMatrix, classLabels): m,n = shape(dataMatrix) alpha = 0.01 weights = ones(n) #initialize to all ones for i in range(m): h = sigmoid(sum(dataMatrix[i]*weights)) error = classLabels[i] - h weights = weights + alpha * error * dataMatrix[i] return weights def stocGradAscent1(dataMatrix, classLabels, numIter=150): # m,n = shape(dataMatrix) weights = ones(n) #initialize to all ones for j in range(numIter): dataIndex = range(m) for i in range(m): alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not # 学习率越来越低 randIndex = int(random.uniform(0,len(dataIndex))) # go to 0 because of the constant h = sigmoid(sum(dataMatrix[randIndex]*weights)) # 随机选择样本 error = classLabels[randIndex] - h weights = weights + alpha * error * dataMatrix[randIndex] del(dataIndex[randIndex]) return weights def classifyVector(inX, weights): prob = sigmoid(sum(inX*weights)) if prob > 0.5: return 1.0 else: return 0.0
1. 线性回归
假设 特征 和 结果 都满足线性。即不大于一次方。这个是针对 收集的数据而言。
收集的数据中,每一个分量,就可以看做一个特征数据。每个特征至少对应一个未知的参数。这样就形成了一个线性模型函数,向量表示形式:
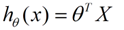
这个就是一个组合问题,已知一些数据,如何求里面的未知参数,给出一个最优解。 一个线性矩阵方程,直接求解,很可能无法直接求解。有唯一解的数据集,微乎其微。
基本上都是解不存在的超定方程组。因此,需要退一步,将参数求解问题,转化为求最小误差问题,求出一个最接近的解,这就是一个松弛求解。
求一个最接近解,直观上,就能想到,误差最小的表达形式。仍然是一个含未知参数的线性模型,一堆观测数据,其模型与数据的误差最小的形式,模型与数据差的平方和最小:
这就是损失函数的来源。接下来,就是求解这个函数的方法,有最小二乘法,梯度下降法。
最小二乘法
是一个直接的数学求解公式,不过它要求X是列满秩的,
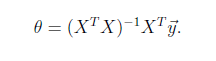
梯度下降法
分别有梯度下降法,批梯度下降法,增量梯度下降。本质上,都是偏导数,步长/最佳学习率,更新,收敛的问题。这个算法只是最优化原理中的一个普通的方法,可以结合最优化原理来学,就容易理解了。
2. 逻辑回归
逻辑回归与线性回归的联系、异同?
逻辑回归的模型 是一个非线性模型,sigmoid函数,又称逻辑回归函数。但是它本质上又是一个线性回归模型,因为除去sigmoid映射函数关系,其他的步骤,算法都是线性回归的。可以说,逻辑回归,都是以线性回归为理论支持的。
只不过,线性模型,无法做到sigmoid的非线性形式,sigmoid可以轻松处理0/1分类问题。
另外它的推导含义:仍然与线性回归的最大似然估计推导相同,最大似然函数连续积(这里的分布,可以使伯努利分布,或泊松分布等其他分布形式),求导,得损失函数。
![\begin{align}J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^m y^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) \right]\end{align}](http://deeplearning.stanford.edu/wiki/images/math/f/a/6/fa6565f1e7b91831e306ec404ccc1156.png)
逻辑回归函数
 表现了0,1分类的形式。
表现了0,1分类的形式。
应用举例:
是否垃圾邮件分类?
是否肿瘤、癌症诊断?
是否金融欺诈?
3. 一般线性回归:
http://deeplearning.stanford.edu/wiki/index.php/Softmax_Regression
线性回归 是以 高斯分布 为误差分析模型; 逻辑回归 采用的是 伯努利分布 分析误差。而高斯分布、伯努利分布、贝塔分布、迪特里特分布,都属于指数分布。
![]()
而一般线性回归,在x条件下,y的概率分布 p(y|x) 就是指 指数分布. 经历最大似然估计的推导,就能导出一般线性回归的 误差分析模型(最小化误差模型)。
softmax回归就是 一般线性回归的一个例子。
有监督学习回归,针对多类问题(逻辑回归,解决的是二类划分问题),如数字字符的分类问题,0-9,10个数字,y值有10个可能性。
而这种可能的分布,是一种指数分布。而且所有可能的和 为1,则对于一个输入的结果,其结果可表示为:
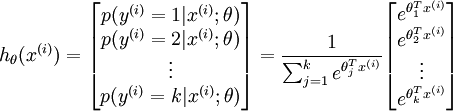 参数是一个k维的向量。而代价函数:
参数是一个k维的向量。而代价函数:![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]\end{align}](http://deeplearning.stanford.edu/wiki/images/math/7/6/3/7634eb3b08dc003aa4591a95824d4fbd.png)
是逻辑回归代价函数的推广。而对于softmax的求解,没有闭式解法(高阶多项方程组求解),仍用梯度下降法,或L-BFGS求解。当k=2时,softmax退化为逻辑回归,这也能反映softmax回归是逻辑回归的推广。
4. 拟合:拟合模型/函数
由测量的数据,估计一个假定的模型/函数。如何拟合,拟合的模型是否合适?可分为以下三类
合适拟合
欠拟合
过拟合
过拟合的问题如何解决?
问题起源?模型太复杂,参数过多,特征数目过多。
方法: 1) 减少特征的数量,有人工选择,或者采用模型选择算法 :http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html (特征选择算法的综述)
2) 正则化,即保留所有特征,但降低参数的值的影响。正则化的优点是,特征很多时,每个特征都会有一个合适的影响因子。
5. 概率解释:线性回归中为什么选用平方和作为误差函数?
假设模型结果与测量值 误差满足,均值为0的高斯分布,即正态分布。这个假设是靠谱的,符合一般客观统计规律。
数据x与y的条件概率:
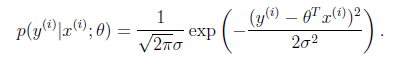
若使 模型与测量数据最接近,那么其概率积就最大。概率积,就是概率密度函数的连续积,这样,就形成了一个最大似然函数估计 。对最大似然函数估计进行推导,就得出了求导后结果: 平方和最小公式
。对最大似然函数估计进行推导,就得出了求导后结果: 平方和最小公式
7. 错误函数/代价函数/损失函数:
线性回归中采用平方和的形式,一般都是由模型条件概率的最大似然函数 概率积最大值,求导,推导出来的。
统计学中,损失函数一般有以下几种:
1) 0-1损失函数
L(Y,f(X))={1,0,Y≠f(X)Y=f(X)
2) 平方损失函数
L(Y,f(X))=(Y−f(X))2
3) 绝对损失函数
L(Y,f(X))=|Y−f(X)|
4) 对数损失函数
L(Y,P(Y|X))=−logP(Y|X)
损失函数越小,模型就越好,而且损失函数 尽量 是一个凸函数,便于收敛计算。
线性回归,采用的是平方损失函数。而逻辑回归采用的是 对数 损失函数。 这些仅仅是一些结果,没有推导。
正则化:
为防止过度拟合的模型出现(过于复杂的模型),在损失函数里增加一个每个特征的惩罚因子。这个就是正则化。如正则化的线性回归 的 损失函数:
lambda就是惩罚因子。
正则化是模型处理的典型方法。也是结构风险最小的策略。在经验风险(误差平方和)的基础上,增加一个惩罚项/正则化项。线性回归的解,也从θ=(XTX)−1XTy
转化为
括号内的矩阵,即使在样本数小于特征数的情况下,也是可逆的。逻辑回归的正则化:
从贝叶斯估计来看,正则化项对应模型的先验概率,复杂模型有较大先验概率,简单模型具有较小先验概率。这个里面又有几个概念。什么是结构风险最小化?先验概率?模型简单与否与先验概率的关系?
经验风险、期望风险、经验损失、结构风险
期望风险(真实风险),可理解为 模型函数固定时,数据 平均的 损失程度,或“平均”犯错误的程度。 期望风险是依赖损失函数和概率分布的。只有样本,是无法计算期望风险的。
所以,采用经验风险,对期望风险进行估计,并设计学习算法,使其最小化。即经验风险最小化(Empirical Risk Minimization)ERM,而经验风险是用损失函数来评估的、计算的。对于分类问题,经验风险,就训练样本错误率。对于函数逼近,拟合问题,经验风险,就平方训练误差。对于概率密度估计问题,ERM,就是最大似然估计法。
而经验风险最小,并不一定就是期望风险最小,无理论依据。只有样本无限大时,经验风险就逼近了期望风险。如何解决这个问题? 统计学习理论SLT,支持向量机SVM就是专门解决这个问题的。有限样本条件下,学习出一个较好的模型。由于有限样本下,经验风险Remp[f]无法近似期望风险R[f] 。因此,统计学习理论给出了二者之间的关系:R[f] <= ( Remp[f] + e )
而右端的表达形式就是结构风险,是期望风险的上界。而e = g(h/n)是置信区间,是VC维h的增函数,也是样本数n的减函数。VC维的定义在 SVM,SLT中有详细介绍。e依赖h和n,若使期望风险最小,只需关心其上界最小,即e最小化。所以,需要选择合适的h和n。这就是结构风险最小化Structure Risk Minimization,SRM. SVM就是SRM的近似实现,SVM中的概念另有一大筐。就此打住。
1范数,2范数 的物理意义:
范数,能将一个事物,映射到非负实数,且满足非负性,齐次性,三角不等式。是一个具有“长度”概念的函数。
1范数为什么能得到稀疏解?
压缩感知理论,求解与重构,求解一个L1范数正则化的最小二乘问题。其解正是 欠定线性系统的解。
2范数为什么能得到最大间隔解?
2范数代表能量的度量单位,用来重构误差。
以上几个概念理解需要补充。
牛顿法求解 最大似然估计
前提条件:求导迭代,似然函数可导,且二阶可导。
迭代公式: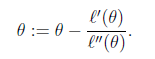
若是 向量形式,
![]()
H就是 n*n 的hessian矩阵了。
特征:当靠近极值点时,牛顿法能快速收敛,而在远离极值点的地方,牛顿法可能不收敛。 这个的推导?
这点是与梯度下降法的收敛特征是相反的。
核函数的物理意义:
映射到高维,使其变得线性可分。什么是高维?如一个一维数据特征x,转换为(x,x^2, x^3),就成为了一个三维特征,且线性无关。一个一维特征线性不可分的特征,在高维,就可能线性可分了。
Regression问题的常规步骤为:
- 寻找h函数(即hypothesis);
- 构造J函数(损失函数);
- 想办法使得J函数最小并求得回归参数(θ)
构造预测函数h
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为:
Sigmoid 函数在有个很漂亮的“S”形,如下图所示(引自维基百科):
下面左图是一个线性的决策边界,右图是非线性的决策边界。
对于线性边界的情况,边界形式如下:
构造预测函数为:
函数的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
构造损失函数J
Cost函数和J函数如下,它们是基于最大似然估计推导得到的。
下面详细说明推导的过程:
(1)式综合起来可以写成:
取似然函数为:
对数似然函数为:

最大似然估计就是求使 取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将
取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将 取为下式,即:
取为下式,即:

因为乘了一个负的系数-1/m,所以取 最小值时的θ为要求的最佳参数。
最小值时的θ为要求的最佳参数。
梯度下降法求的最小值
θ更新过程:


θ更新过程可以写成:

向量化Vectorization
Vectorization是使用矩阵计算来代替for循环,以简化计算过程,提高效率。
如上式,Σ(...)是一个求和的过程,显然需要一个for语句循环m次,所以根本没有完全的实现vectorization。
下面介绍向量化的过程:
约定训练数据的矩阵形式如下,x的每一行为一条训练样本,而每一列为不同的特称取值:

g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。由上式可知 可由
可由 一次计算求得。
一次计算求得。
θ更新过程可以改为:

综上所述,Vectorization后θ更新的步骤如下:
(1)求 ;
;
(2)求 ;
;
(3)求  。
。
Reference: