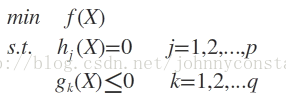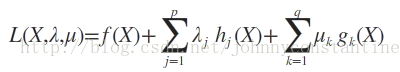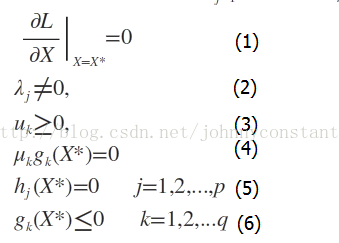SVM相关知识及和softmax区别
1.相对于容易过度拟合训练样本的人工神经网络,支持向量机对于未见过的测试样本具有更好的推广能力。
2.SVM更偏好解释数据的简单模型---二维空间中的直线,三维空间中的平面和更高维空间中的超平面。
3.SVM正是从线性可分情况下的最优分类面发展而来,主要思想就是寻找能够成功分开两类样本并且有最大分类间隔的最优分类超平面。算法最终转化为二次型寻优问题,得到的是全局最优,解决了在神经网络方法中无法避免的局部极值问题。
三类:对于样本中只有支持向量(SV)对超平面的划分有贡献,所以样本可由支持向量代替。(一般支持向量总是远远少于样本总数)
线性可分的SVM
非线性可分的SVM(C-SVM) 引入错误代价系数C
需要核函数映射情况下的SVM (通过非线性变换将其转化为某个高维空间中的线性问题) ---有个点积运算,可用核函数代替
核函数:
Kernel 函数满足Mercer条件,它就对应某一变换空间中的内积。
多类问题:
1 一对多的最大响应策略
2 一对一的投票策略
3 一对一的淘汰策略
(3)不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下:
则我们定义不等式约束下的拉格朗日函数L,则L表达式为:
其中f(x)是原目标函数,hj(x)是第j个等式约束条件,λj是对应的约束系数,gk是不等式约束,uk是对应的约束系数。0
此时若要求解上述优化问题,必须满足下述条件(也是我们的求解条件):
这些求解条件就是KKT条件。(1)是对拉格朗日函数取极值时候带来的一个必要条件,(2)是拉格朗日系数约束(同等式情况),(3)是不等式约束情况,(4)是互补松弛条件,(5)、(6)是原约束条件。
对于一般的任意问题而言,KKT条件是使一组解成为最优解的必要条件,当原问题是凸问题的时候,KKT条件也是充分条件。
关于条件(3),后面一篇博客中给出的解释是:我们构造L(x,λ,u)函数,是希望L(x,λ,u)<=f(x)的(min表示求最小值)。在L(x,λ,u)表达式中第二项为0,若使得第三项小于等于0就必须使得系数u>=0,这也就是条件(3)。
关于条件(4),直观的解释可以这么看:要求得L(x,λ,u)的最小值一定是三个公式项中取得最小值,此时第三项最小就是等于0值的时候。稍微正式一点的解释,是由松弛变量推导而来。
参考: 支持向量机(SVM)复习总结
支持向量机原理(五)线性支持回归(待填坑)