SNE+t-SNE+拉普拉斯矩阵

SNE是通过仿射(affinitie)变换将数据点映射到概率分布上，主要包括两个步骤：

• SNE构建一个高维对象之间的概率分布，使得相似的对象有更高的概率被选择，而不相似的对象有较低的概率被选择。
• SNE在低维空间里在构建这些点的概率分布，使得这两个概率分布之间尽可能的相似。

我们看到t-SNE模型是非监督的降维，他跟kmeans等不同，他不能通过训练得到一些东西之后再用于其它数据（比如kmeans可以通过训练得到k个点，再用于其它数据集，而t-SNE只能单独的对数据做操作，也就是说他只有fit_transform，而没有fit操作）

t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法，是由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出来。此外，t-SNE 是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化。

t-SNE是由SNE(Stochastic Neighbor Embedding, SNE; Hinton and Roweis, 2002)发展而来。我们先介绍SNE的基本原理，之后再扩展到t-SNE。最后再看一下t-SNE的实现以及一些优化。

一、拉普拉斯矩阵基本定义

对于图G，一般用点的集合V和边的集合E来描述：G（V,E）。现在有这样一个图，如何定义拉普拉斯矩阵呢？这里涉及到两个常用矩阵：邻接矩阵、度矩阵。

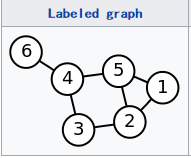
从最简单的应用入手，不同数据点相通权重为1，不相通权重为0.

首先求解邻接矩阵W：

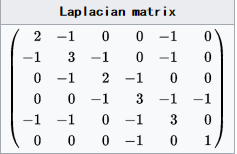
将每一列求和，这个数值的对角形式对应就是度矩阵D：

i=∑j=1nwij

写成矩阵形式：⎜⎜⎜d1…⋮……d2⋮………⋱dn⎞⎠⎟⎟⎟⎟⎟

从而得到拉普拉斯矩阵L的定义：

L=D−W

 

二、拉普拉斯矩阵意义及性质

f

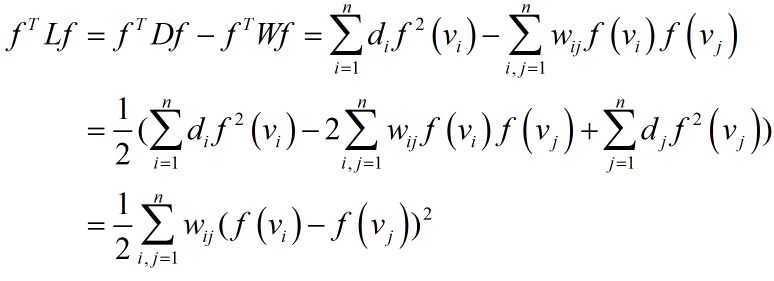
0=λ1　≤λ2　≤...　≤　λn

• t-SNE完整笔记

• 拉普拉斯矩阵（Laplace Matrix）与瑞利熵（Rayleigh quotient）