2019/8/1 LCA(最近公共祖先) (2)
LCA(最近公共祖先)
LCA,Lowest Common Ancetors,即最近公共祖先。
有关LCA定义及示例详见上一篇LCA(RMQ)。
今天向大家介绍的是LCA(Tarjan)算法
Tarjan求解LCA
前置知识
-
并查集
-
链式前向星
-
DFS
梗概:Tarjan求解LCA是利用DFS的性质在对给定树进行遍历时不断更新一给定询问结点在目前遍历高度的祖先,当遍历到另一询问节点时查找前一询问节点祖先,以此求出给定两点LCA。
时间复杂度:O(n+q) q:询问次数
1.在线/离线算法
在线算法:
“在计算机科学中,一个在线算法是指它可以以序列化的方式一个个的处理输入,也就是说在开始时并不需要已经知道所有的输入。”------百度百科
离线算法:
“算法设计策略都是基于在执行算法前输入数据已知的基本假设,也就是说,对于一个离线算法,在开始时就需要知道问题的所有输入数据,而且在解决一个问题后就要立即输出结果,通常将这类具有问题完全信息前提下设计出的算法称为离线算法( off line algorithms)”------百度百科
本文介绍的Tarjan求解LCA算法是一种离线算法,其需要将询问储存起来集中处理,得到答案后一并输出。
2.Tarjan
“Robert Tarjan,计算机科学家,以LCA、强连通分量等算法闻名。”------百度百科
Tarjan(求LCA)算法基于DFS原理。利用LCA必然存在于从一询问节点至另一询问结点的DFS遍历路径上的性质,回答询问。
又是这棵树(再次手残)
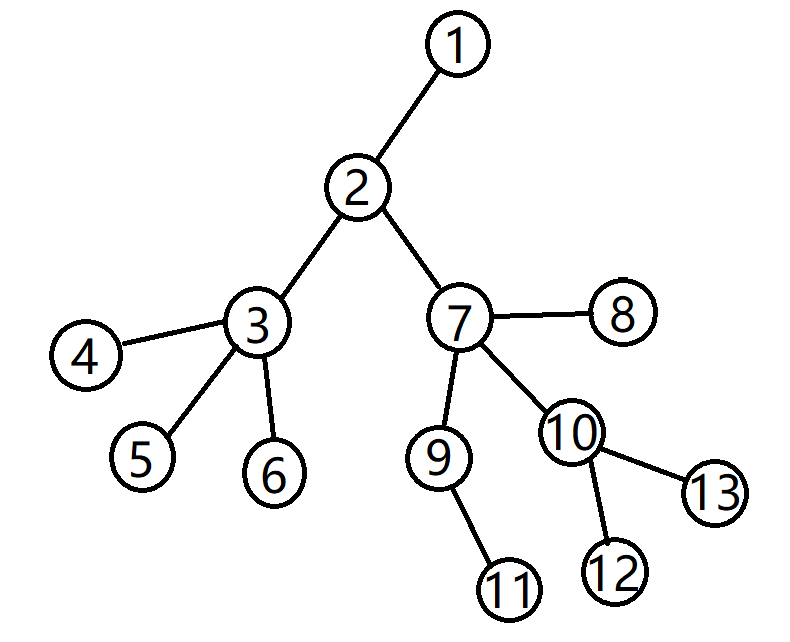
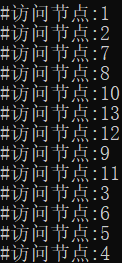
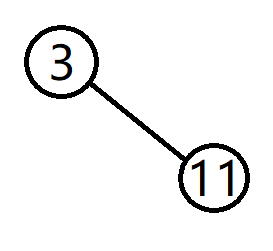
给定树 访问路径 “询问”树
首先,读入整颗给定树,建树,读入所有询问(3 11),建立“询问树”。
对于询问结点3与结点11,假定我们按照顺序遍历了除结点11外结点7的子树中所有结点。
示例流程(具体代码见“实现”部分):
1.将结点11标记为已访问。
2.枚举结点11所有出边。
3.由于结点11无未访问的出边指向的点,开始遍历结点11在“询问”树中所有的出边。
4.出边指向结点3,由于节点3未访问,直接跳过。
5.回溯至结点9,继续访问结点9的出边,发现遍历完成,更新f[11]=9,回溯。
6.重复第5步直至访问结点2,更新f[7]=2,继续遍历结点2出边,访问未遍历节点3。
7.重复第1至5步,直至遍历完结点3的所有出边。
8.结点3无未遍历出边,开始遍历结点3在“询问树”中的出边。
9.出边指向已访问节点11,查找结点11的祖先。
10.由于还未回溯至结点1,所以f[2]还未更新为1,此时仍为2,即f[11]=f[9]=f[7]=f[2]=2。
11.结点2即为询问(3 11)的LCA。
以上即是此种算法求LCA的基本步骤,在实现时,可归纳为
1.标记结点为已访问。
2.遍历所有出边,如指向结点为访问则继续递归。
3.回溯,更新父亲节点。(基于并查集)
4.遍历结点在“询问”树中所有出边,如指向结点已访问,存储指向结点祖先为此次询问结果。
至此,原理分析结束。(如仍有疑问请看“实现”部分)
3.实现
代码:
声明部分:
1 #include <iostream> 2 #include <cstdio>//标准输入输出 3 using namespace std; 4 int n,m,s,cnt;//cnt为边计数器 5 int head[500005];//链式前向星 6 int qhead[500005];//链式前向星 (询问) 7 int f[500005];//并查集储存父结点 8 int vis[500005];//判断是否访问过 9 int lca[1000005];//离线存储答案
链式前向星部分:
1 struct edge 2 { 3 int nxt; 4 int to; 5 //int dis;边权值默认为 1 6 }e[1000005];//建议4倍 7 8 struct qedge 9 { 10 int nxt; 11 int to; 12 //int dis; 13 }qe[1000005];//建议4倍 14 15 void add(int x,int y/*,int d*/) 16 { 17 e[++cnt].nxt=head[x]; 18 e[cnt].to=y; 19 head[x]=cnt; 20 }//链式前向星加边 21 22 void qadd(int x,int y) 23 { 24 qe[++cnt].nxt=qhead[x]; 25 qe[cnt].to=y; 26 qhead[x]=cnt; 27 }//链式前向星加边 (询问)
并查集模板部分:
1 int find(int x) 2 { 3 return f[x]== x ? x : f[x] = find( f[x] );//路径压缩 4 }//“查 ” 5 6 void merge(int a,int b) 7 { 8 int fa=find(a),fb=find(b); 9 if(fa==fb) 10 return ; 11 f[fa]=fb; 12 }//“并 ” 13 14 void setup(int N) 15 { 16 for(int i=1;i<=N;i++) 17 { 18 f[i]=i; 19 } 20 }//初始化
Tarjan(DFS)函数部分:
1 void tarjan(int x) 2 { 3 cout<<"#访问节点:"<<x<<endl; 4 vis[x]=1;//标记访问 5 for(int i=head[x];i;i=e[i].nxt)//遍历此子节点所有出边 6 { 7 int v=e[i].to; 8 if(!vis[v])//如下一节点未访问 9 { 10 tarjan(v);//继续遍历 11 f[v]=x;//回溯时更新子节点祖先 12 if(v==11) 13 { 14 cout<<"//"<<x<<" "<<f[11]<<endl; 15 } 16 } 17 } 18 for(int i=qhead[x];i;i=qe[i].nxt)//对于询问中有此点的询问组 19 { 20 int qv=qe[i].to; 21 if(vis[qv])//若另一询问节点已被遍历 22 { 23 lca[i]=find(qv);//则对于这组询问,其LCA为另一询问节点最后一次更新的祖先 24 if(i%2)//对于正反两组相同询问 25 lca[i+1]=lca[i];//若为正向的询问,下一组询问为此次询问的反向询问 ,询问结果相同 26 else 27 lca[i-1]=lca[i];//若为反向的询问,下一组询问为此次询问的正向询问 ,询问结果相同 28 } 29 } 30 }//DFS函数
主函数:
1 int main() 2 { 3 cin>>n>>m>>s; 4 for(int i=1;i<n;i++) 5 { 6 int a,b; 7 cin>>a>>b; 8 add(a,b);//无向图正反存边 9 add(b,a); 10 } 11 cnt=0;//懒得再加一个变量qcnt 12 for(int i=1;i<=m;i++) 13 { 14 int a,b; 15 cin>>a>>b; 16 qadd(a,b);//储存正反询问 17 qadd(b,a);//无向图正反存边 18 } 19 setup(n);//初始化 20 tarjan(s);//以s为根开始遍历 21 for(int i=1;i<=m;i++) 22 { 23 printf("%d\n",lca[i*2]);//由于每组询问储存了两遍,所以输出时输出其中一组 24 } 25 return 0; 26 }
结语:
Tarjan好啊!!!
相关题目:
见上一篇末。
//还没想起来·······
over.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号