词法分析原理 - Lexical Analysis

Regex, DFA, NFA 算法理论

算法1：根据Regex构建NFA - McNaughton-Yamada-Thompson Construction

输入：字母表∑上的一个正则表达式r。
输出：一个接受L(r)的NFA N。
方法：首先对r进行语法分析，分解出组成它的子表达式。构建NFA的规则分为基本规则和归纳规则。
基本规则：处理不包含运算符的子表达式。
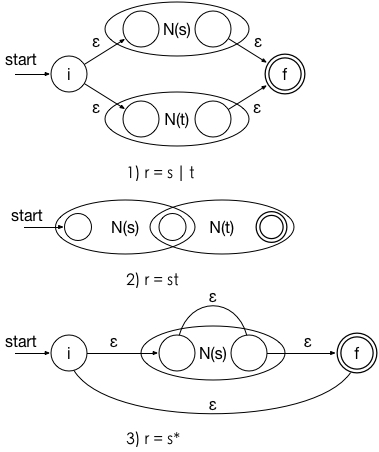
　　对于表达式ε，构造如下NFA：[ start ]---->[ i ]--(ε)-->[[ f ]]。其中i和f都是新状态，分别为起始状态和接受状态。
　　对于表达式a，构造如下NFA：[ start ]---->[ i ]--(a)-->[[ f ]]。其中i和f都是新状态，分别为起始状态和接受状态。
　　对于每次ε或a作为r的子表达式出现，都会用新状态构建一个独立的NFA。
归纳规则：根据给定表达式r的直接子表达式的NFA构造总NFA。
　　假设正则表达式s和t的NFA分别为N(s)和N(t)，可如图根据三种情况构建r的DFA。
　　

算法2：根据NFA构建等价DFA - 子集构造算法 - The Subset Construction

输入：一个NFA N。
输出：一个等价的DFA D。
方法：DFA的每个状态是一个NFA的状态集合，构造DFA转换方程Dtran，使得DFA并行地模拟NFA遇到给定输入串时可能执行的所有动作。首先定义如下操作，其中s表示NFA的单个状态，T表示NFA的一个状态集合。

ε-closure(s): 能够从NFA状态s开始，只通过ε转换到达的NFA状态集合。
ε-closure(T): 能够从NFA的状态集T中某个状态s开始，只通过ε转换到达的NFA状态集合。
move(T, a): 能够从NFA的状态集T中某个状态s开始，通过标记为a的转换到达的NFA状态集合。

算法：初始状态可能是ε-closure(s₀)中的任意状态，其中s₀是NFA的起始状态。读入输入符号a后，NFA可以立即移动到move(T, a)中任何状态，同样可以进一步移动到ε-closure(move(T, a))中的任何状态。

子集构造法:
一开始，ε-closure(s0)是Dstates中的唯一状态，且未标记;
while (在Dstates中有一个为标记状态T) {
    标记T;
    for (每个字母表中符号a) {
        U = ε-closure(move(T, a));
        if (U不在Dstates中)
            将未标记的U加入到Dstates中;
        Dtran[T, a] = U;
    }
}

计算ε-closure(T):
将T的所有状态压入栈stack中, 将ε-closure(T)初始化为T;
while (stack不为空) {
    t = stack.pop;
    for (每个满足如下条件的u: 从t出发有一个标号为的转换到达状态u)
        if (u不在ε-closure(T)中) {
            将u加入到ε-closure(T)中;
            将u压入栈中;
        }
}

算法3：模拟NFA执行过程

输入：一个以eof结尾的输入串x，一个NFA N，开始状态为s₀，接受状态集为F，转换函数为move。
输出：接受串x则返回yes，否则返回no。
方法：保存一个当前状态集合S，即可以从开始状态沿着标号到当前已读入的输入部分的路径到达状态的集合。如果c是函数nextChar()读到的下一个输入字符，那么就首先计算move(S, c)，然后通过ε-closure()求闭包。

模拟NFA执行过程:
S = ε-closure(s0);
c = nextChar();
while (c != eof) {
    S = ε-closure(move(S, c));
    c = nextChar();
}
if (S ∩ F != Ø) return yes;
else return no;

算法4：直接通过Regex创建DFA

重要状态：如果一个NFA状态有离开转换，且都不是基于ε的转换，则该状态为重要状态。NFA重要状态直接对应于regex中符号的位置。

过程函数：这些函数基于增广正则表达式(r)#所构成的抽象语法树。
　　1) nullable(n)，该节点所代表的子表达式对应的语句包含ε语句，则为真。
　　2) firstpos(n)，可以出现在该节点表达的语句的第一个位置的符号。
　　3) lastpos(n)，可以出现在该节点表达的语句的最后一个位置的符号。
　　4) followpos(p)，可以出现在p所代表的语句的后面的第一个字符。
a) 计算nullable, firstpos, lastpos
　　可以根据语法树，自底向上递归获得。
b) 计算followpos
　　只有两种情况会使得一个regex的某个位置跟在另一个位置之后：
　　1) 如果n是一个cat结点，左右子节点为c₁、c₂，那么对于lastpos(c₁)中的每个位置i，followpos(i) = firstpos(c₂)；
　　2) 如果n是star结点，对于lastpos(n)中的每个位置i，followpos(i) = firstpos(n)。

输入：一个regex r。
输出：一个识别L(r)的DFA D。
方法：
　　1) 根据扩展正则表达式(r)#构造语法树T。
　　2) 计算函数nullable(), firstpos(), lastpos()和followpos()。
　　3) 根据如下算法构造：

从Regex构造DFA:
初始化Dstates, 使其只包含未标记状态集firstpos(n0), 其中n0是T的根节点;
while (Dstates存在未标记状态集S) {
    标记S；
    for (每个输入符号a) {
        令U为S中和a对应的所有位置p的followpos(p)的并集;
        if (U不在Dstates中)
            将未标记的U加入Dstates;
        Dtran[S, a] = U;
    }
}

算法5：最小化DFA - Hopcroft's Algorithm

DFA的等价状态：对于任意输入串产生同样状态。
方法：首先粗划分为两组p₀ = D_accept，p₁ = {D - D_accpet}。对于p_s中的状态d_i和d_j，他们必须满足 ∀c∈Σ, δ(i, c) = x, δ(j, c) = y 且 d_x, d_y ∈ p_t。为了划分P，该算法检查每一个p∈P以及每一个c∈Σ。如果c划分p，该算法就将p划分为两个子集并添加至T中。
创建DFA：根据等价状态分组，对于每一组状态集p∈P，在DFA中对应建立一个状态。对于d_j∈p_l，d_k∈p_m，且δ(d_j, c) = d_k，我们就创建两个状态分别对应pl和pm，且δ(p_l, c) = p_m。

DFA等价状态划分:
T = {Da, {D - Da}};
P = ø;
while (P != T) {
    P = T;
    T = ø;
    for (each set p ∈ P)
        T = T ∪ Split(p);
}
Split(S) {
    for (each c ∈ Σ) {
        if (c splits S into s1 and s2)
            then return {s1, s2};
    }
    return S;
}

算法6：直接从NFA构建最小化DFA - Brzozowski's Algorithm

应当注意到在子集构建DFA时，不会有相同前缀出现。该算法运用了这一特性，直接从NFA构建最小化DFA。

对于给定NFA N：
　　reverse(N): 将NFA倒转，将所有原接受状态连接至新的起始状态。
　　reachable(N): 所有从起始状态可以到达的状态。
　　subset(N): 子集构建法获得的DFA。

于是可得NFA N对应的最小化DFA为：
　　reachable(subset(reverse( reachable(subset(reverse(n))) )))

其中，内部的subset(reverse(n))精简了NFA的后缀，reachable()弃掉了所有无用的状态。然后外部的三个函数再一次精简了NFA的前缀，并弃掉其余无用状态，最终构建最小化NFA。

将DFA转化为代码实现

实现1：表驱动分析器 - Table-Driben Scanner

方法：将转换函数输入到一个对应的二维数组中，scan过程中通过查表来模拟DFA行为。还可以提供另外一个表用来将输入字符分类，实现压缩转换表。

Table-Driven Scanner:
Nextword() {
　　 /* initalization */
    state = S0;
    lexeme = "";
    stack.clear();
    stack.push(bad);
    /* scanning loop to model the DFA's behavior */
    while (state != Serror) {
        char = Nextchar();
        lexeme += char;
        if (state ∈ Saccept)
            stack.clear();
        stack.push(state);
        category = CharCat[char];　　// 表1: 字符分类表, e.g. digit, letter, punc, space
        state = δ[state, cat];　　　 // 表2: 转换表, 包含每个状态下对应不同输入的转换状态
    }
    /* roll back loop in case the DFA overshoots the end of the token */
    while (state ∉ Saccept && state != bad) {
        stack.pop();
        truncate lexeme;
        RollBack();
    }
　　 /* interprets and reports the result */
    if (state ∈ Saccept)
        return Type[state];
    else return invalid;
}

实现2：直接编码分析器 - Direct-Coded Scanners

方法：直接将转换表的行为编入代码，节省查表时间。

Sinit: lexeme = "";
         stack.clear();
         stack.push(bad);
         goto S0;
S0:    Nextchar(char);
         lexeme += char;
         if (state ∈ Saccept)
             stack.clear();
         stack.push(state);
         if (char == 'r')
             goto S1;
         else goto Sout;
S1:    ...
S2:    ...
Sout: while (state ∉ Saccept && state != bad) {
             state = stack.pop();
             truncate lexeme;
             RollBack();
         }
         if (state ∈ Saccept)
              then return Type[state];
         return invalid;

实现3：手工构建分析器 - hand-Coded Scanner

方法：利用双重缓冲技术，通过指针高效读取输入字符。

initialization:
Input = 0;
Fence = 0;
fill Buffer[0 : n];

implementing NextChar():
Char = Buffer[Input];
Input = (Input + 1) mod 2n;
if (Input mod n == 0) {
    fill Buffer[Input : Input + n - 1];
    Fence = (Input + n) mod 2n;
}
return Char;

implementing RollBack():
if (Input == Fence)
    then signal roll back error;
Input = (Input - 1) mod 2n;