斐波那契堆简介
斐波那契堆(Fibnacci Heap)有两种用途:第一,支持一系列操作,这些操作构成了所谓的可合并堆。第二,其一些操作可以在常数时间内完成,这使得这种数据结构非常适合于需要频繁调用这些操作的应用。
可合并堆(Mergeable Heap)支持如下五种操作:Make-Heap(), Insert(H, x), Minmun(H), Extract-Min(H), Union(H1, H2)。事实上,就是具备了快速合并操作的堆(Heap)。
斐波那契堆还支持额外两种操作:Decrease-Key(H, x, k), Delete(H, x)。
斐波那契堆结构
一个斐波那契堆是一系列具有最小堆序的有根树集合,每棵树都遵循最小堆性质。如图:
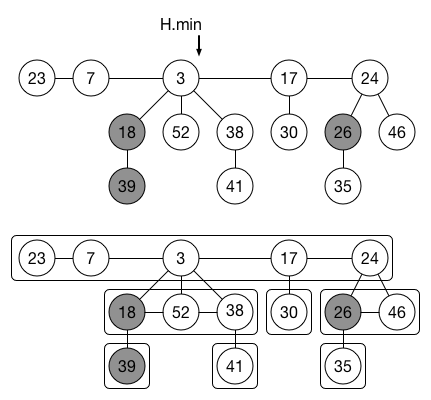
堆属性:
每个结点 x 包含一个指向其父节点的指针 x.parent 和一个指向其某一个孩子的指针 x.child,x 的所有构成了一个双向环形链表,称之为 x 的孩子链表。每个孩子节点 y 包含指针 y.left 和 y.right 指向兄弟节点。孩子链表中各兄弟出现的次序是任意的。
每个结点还有两个属性。把结点 x 的孩子链表中的孩子数目存储在 x.degree 中,布尔值属性 x.mark 指示结点 x 自上一次成为另一个结点的孩子后,是否是去过孩子。新节点是未被标记的,当结点 x 成为另一个结点的孩子时,便成为未被标记结点。
通过指针 H.min 来访问一个给定的斐波那契堆 H,指向该堆的最小根节点。如果堆为空,则 H.min 指向 NULL。因为根节点也构成了双向环形链表,所以根节点的次序是任意的。
根节点还有一个属性 H.n 表示当前节点数目。
势函数:
通过势函数来分析斐波那契堆性能。对于给定堆 H, 用 t(H) 表示 H 中根链表中树的树木,用 m(H) 来表示 H 中已标记结点的树木。定义斐波那契堆 H 的势函数 Φ(H) = t(H) + 2m(H)。
最大度数:
在一个 n 个结点的斐波那契堆中任何结点的最大度数都有上界 D(n)。如果仅仅支持可合并堆操作,那么 D(n) ≤ floor(lgn),当支持斐波那契堆操作时,也要求 D(n) = O(lgn)。
可合并堆操作
斐波那契堆上的一些可合并操作应尽可能延后执行。不同的操作可以进行性能平衡。例如,当执行 Extract-Min 操作后,不得不遍历根链表剩下的结点找出新的最小结点。这里便存在性能平衡问题。只要我们在执行 Extract-Min 操作后便利整个根链表,并把结点合并到最小堆序树中以减小根链表的规模。后面将讨论到,不论执行 Extract-Min 之前是什么样子,执行之后,根链表中每个节点要求有一个唯一的度数,使得根链表规模最大为 D(n)+1。
创建新的斐波那契堆:
创建一个新堆,Make-FibHeap 过程分配并返回一个斐波那契堆对象 H,其中 H.n = 0 和 H.min = NULL,H 中没有树,因为 t(H) = 0 且 m(H) = 0,所以其势 Φ(H) = 0。因此其摊还代价等于其实际代价 O(1)。
插入一个节点:
下面过程将结点 x 插入至 H 中,其中 x.key 已被赋值。
FibHeap-Insert(List *H, Node *x) { x.degree = 0 x.parent = NULL x.child = NULL x.mark = False if (H.min == NULL) create a root list for H containing just x H.min = x else insert x into H's root list if (x.key < H.min.key) H.min = x H.n++ }
势的增加量为 1,实际代价为 O(1),所以摊还代价为 O(1) + 1 = O(1)。
寻找最小节点:
可以通过指针 H.min 直接得到,摊还代价等于实际代价为 O(1)。
两个斐波那契堆合并:
该过程简单地将 H1 和 H2 的根链表链接,然后确定新的 H.min。
FibHeap-Union(List *H1, List *H2) { H = Make-FibHeap() H.min = H1.min concatenate the root list of H2 with that of H1 if ((H1.min == NULL) || (H2.min != NULL && H2.min.key < H1.min.key)) H.min = H2.min H.n = H1.n + H2.n return H }
第1~3行将 H1 和 H2 的根链表链接成为 H 的新根链表。第2~5行设定 H 的最小根节点。第6行设置合并后的节点数目。
势的变化为 0,所以摊还代价等于实际代价 O(1)。
抽取最小结点:
该过程首先将最小节点 H.min 的每个孩子变成根节点,并从根链表中删除该结点。然后合并相同度数结点,优化根链表(这一步操作一直延迟到 Extract-Min 后才执行)。
FibHeap-Extract-Min(List *H) { z = H.min if (z != NULL) for each child x of z add x to the root list of H x.parent = NULL remove z from the root list of H if (z == z.right) H.min = NULL else H.min = z.right Consolidate(H) H.n-- return z }
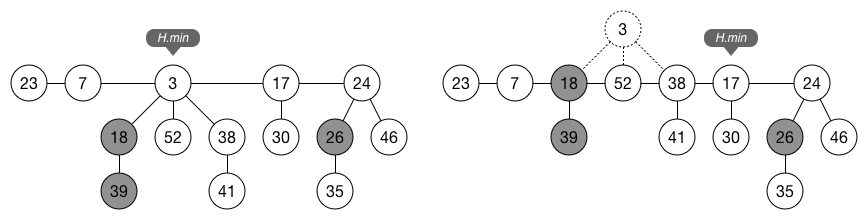
下一步要合并 H 的根链表,通过调用 Consolidate(H) 来减少根链表树的树木。合并过程重复下列过程,直到每个根都具有不同的度数:
1. 在根链表中找到两个相同度数的根 x 和 y,假定 x.key ≤ y.key;
2. 把 y 链接到 x:从根链表移除 y,调用 FibHeap-Link 过程,使 y 成为 x 的孩子。该过程将 x.degree 增加1,并清除 y 上的标记。
过程 Consolidate(H) 使用一个辅助数组 A[0..D(H.n)] 来记录根节点对应度数的轨迹。如果 A[i]=y,那么当前的 y 是一个具有 y.degree=1 的根。计算 D(H.n) 的过程留到后面讲解。
Consolidate(List *H) { create array A[0..D(H,n)] for i = (0 to D(H,n)) A[i] = NULL for each node w in the root list of H x = w d = x.degree while (A[d] != NULL) y = A[d] if (x.key > y.key) exchange x with y FibHeap-Link(H, y, x) A[d] = NULL d++ H.min = NULL for i = (0 to D(H,n)) if A[i] != NULL if H.min == NULL create a root list for H containing just A[i] else insert A[i] into H's root list if A[i].key < H.min.key H.min = A[i] } FibHeap-Link(List *H, Node *y, Node *x) { remove y from the root list of H make y a child of x, incrementing x.degree y.mark = False }
抽取最小节点的摊还代价为 O(lgn)。
斐波那契堆操作-降权和删除
关键字降权:
关键字降权的时候,如果被降权的结点是一个根节点的子节点,则需要判断降权后是否违反最小堆性质。如果子节点比根节点小,则直接将子结点树剪切至斐波那契堆根链表中。如果被剪切子节点的父节点没有标记,则打上标记。如果有标记,则将其父节点也剪切至根链表中,这称之为级联剪切。级联剪切一直向上回溯,直至遇到一个未被标记结点或者根节点。
FibHeap-Decrease-Key(List *H, Node *x, int key) { if (key > x.key) error "New key is greater than current one." x.key = key y = x.parent if (y != NULL && x.key < y.key) Cut(H, x, y) Cacsading-Cut(H, y) if (x.key < H.min.key) H.min = x.key } Cut(List *H, Node *x, Node *y) { remove x from the child list of y, y.degree-- add x to the root list of H x.parent = NULL x.mark = False } Cascading-Cut(List *H, Node *y) { z = y.parent if (z != NULL) if (y.mark == False) y.mark = True else Cut(H, y, z) Cascading-Cut(H, z) }
关键字降权的摊还代价至多为 O(1)。之所以之前有2倍于节点数目的势,一个单位的势支付切断和标记位的清除,另一个单位补偿了被剪切结点成为根节点后多出来的势。
删除节点:
非常简单,降权至-∞后直接 Extract 出去。
FibHeap-Delete(List *H, Node *x) { FibHeap-Decrease-Key(H, x, -∞) FibHeap-Extract-Min(H) }
斐波那契堆理论分析
对于斐波那契堆中的每个结点 x,定义 size(x) 为以 x 为根的子树中包括 x 本身在内的结点个数。我们将证明 size(x) 是 x.degree 的幂。
引理1:设 x 是斐波那契堆中的任意结点,假定 x.degree = k。设 y1, y2, ..., yk 表示 x 的孩子,并以他们链入 x 的先后顺序排列,则 y1.degree ≥ 0,且对于 i = 2, 3, ..., k,有 yi.degree ≥ i-2。
引理2:对于所有整数 k ≥ 0,Fibk+2 = 1 + sigma(i = 0, k)Fibi。
引理3:对于所有整数 k ≥ 0,斐波那契数的第 k+2 个数满足 Fibk+2 ≥ φk,其中 φ = (1 + 根号5)/2。
引理4:设 x 是斐波那契堆中的任意结点,并设 k = x.degree,则有 size(x) ≥ Fibk+2 ≥ φk。
引理5:一个 n 个节点的斐波那契堆中任意结点的最大度数 D(n) = O(lgn)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号