问题简介
对于给定文本 T[n] 和模式 P[m]，找到一个位移量 s，使得 T[s + j] = P[j] (0 <= s <= n-m, 1 <= j <= m)，则说明模式 P 在文本 T 中出现且位移为 s。
所以字符串问题就是在给定文本 T 中，找出指定模式 P 出现的所有有效位移的问题。
记号和术语
长度为0的空字符串用 ɛ 表示。字符串 x 的长度用 |x| 表示。字符串 x, y 的连接表示为xy，长度为 |x|+|y|。
对于字符串 x, y, w，如果 x = wy，就说字符串 w 是字符串 x 的前缀，表示为w ⊏ x，且|w| ≤ |x|；字符串y是字符串x的后缀，表示为y ⊐ x，且|y| ≤ |x|。前缀⊏和后缀⊐都是传递关系。
对于空字符串 ɛ，既是任意字符串的前缀，也是任意字符串的后缀。对于任意字符串x, y和任意字符a，x ⊐ y 当且仅当 xa ⊐ ya。
此外，我们把模式 P[m] 的前k个字符组成的前缀 P[1..k] 记为 Pk。因此，有 P0 = ɛ，Pm = P = P[1..m]。类似地，把文本 T[n] 的前缀记为 Tk。
通过这种方法，可以把字符串匹配问题描述为：找出范围为 0 ≤ s ≤ n-m 并满足 P ⊐ Ts+m 的所有位移。
引理（重叠后缀引理）：设字符串 x, y, z 满足关系 x ⊐ z 和 y ⊐ z，即字符串 x 和 y 都是字符串 z 的后缀。
如果 |x| ≤ |y|，则 x ⊐ y；如果 |x| ≥ |y|，则 y ⊐ x；如果 |x| = |y|，则 x = y。如图：
字符串匹配朴素算法
该算法用一个循环来找出所有有效位移，该循环对 n-m+1 个可能的每一个 s 值检查条件 P[1..m] = T[s+1..s+m]。
NAVIE-STRING-MATCHER(T, P) n = length[T] m = length[P] for s = (0 to n-m) if P[1..m] = T[s+1..s+m] ; 这里隐藏了一个嵌套循环 print s
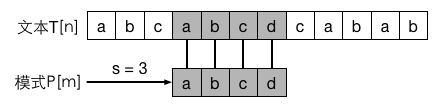
这种朴素算法可以看成用一个包含模式 P 的滑板沿文本 T 滑动，同时判断模式 P 上的字符是否与文本中相应字符相同。如图：
在最坏情况下，朴素算法运行时间为 O((n-m+1)m)。
Rabin-Karp算法
在实际应用中，Rabin-Karp算法能够较好地运行。Rabin-Karp算法预处理时间为 O(m)，在最坏情况下运行时间为 O((n-m+1)m)。但基于某种假设，它的平均情况还是比较好的。为了便于说明，假定字符串字符全集 Σ = {0, 1, 2, ..., 9}，这样每个字符都是一个十进制数字。可以用一个长度为k的十进制数来表示由k个连续字符组成的字符串。例如：字符串12345就可以用十进制数12345表示。
已知一个模式 P[1..m]，设 p 表示其相对应的十进制数的值。类似地，对于给定的文本 T[1..n]，用 ts 来表示其长度为 m 的子字符串 T[s+1..s+m] (s = 0, 1, ..., n-m)相对应的值。
ts = p 当且仅当 T[s+1..s+m] = P[1..m]，当且仅当 ts = p 时，s 是有效位移。如果能在 O(m) 的时间内算出 p 的值，并在总共 O(n-m+1) 的时间内算出所有 ts 的值，那么通过把 p 值与每个 ts 值进行比较，就能在 O(m) + O(n-m+1) = O(n) 时间内求出所有有效位移s。
我们可以运用霍纳法则（Horner's Rule）在 O(m) 时间内计算 p 的值：
$p = P[m] + 10(P[m-1]+10P[m-2]+...+10(P[2]+10P[1])...))$
类似地，也可以在 O(m) 时间内计算 t0 的值。
为了在 O(n-m) 时间内计算出剩余的值 t1, t2, ..., tn-m，可以在常数时间内根据 ts 计算出 ts+1，这是因为
$t_{s+1}=10(t_{s}-10^{m-1}T[s+1])+T[s+m+1]$
例如：如果 m = 5, ts = 31415，我们希望去掉高位数字 T[s+1] = 3，再加入一个低位数字（假设其为 T[s+5+1] = 2）就得到
$t_{s+1}=10(31415-10000\cdot 3)+2=14152$
这个公式可以理解为：减去 10m-1T[s+1] 就从 ts 中减去了高位数字，再把结果乘以10就是数位向左移了一位。然后再加上 T[s+m+1]，就加入了一个适当的低位数。
如果预先计算出常数 10m-1 就能在常数时间内计算出上述结果。因此，可以在 O(m) 时间内计算出 p，在 O(n-m+1) 时间内计算出 t1, t2, ..., tn-m。
因而能够用 O(m) 的与处理时间和 O(n-m+1) 的匹配时间内，进行字符串匹配。
还有一个问题，如果 p 和 ts 太大的话就不能方便的进行处理。可以通过一种简单的方法来补救这一缺点。选取一个合适的模 q 来计算 p 和 ts 的模。所以可以在 O(m) 的时间内计算 p 和 ts 的模，在 O(n-m+1) 时间内计算出所有模 q 的 ts 的值。通常选取 q 为一个素数，使得 10q 正好为一个计算机字长，用单精度预算就可以执行所有必要的运算。一般情况下，采用 d 进制的字母表{0, 1, 2, ..., d-1}时，所选取的 q 要满足dq 的值在一个计算机字长内，并调整先前的递归公式为
$t_{s+1}=(d(t_{s}-T[s+1]h)+T[s+m+1]) \mod q$
其中 h ≡ dm-1 (mod q)，是一个 m 数位文本窗口中最高数位上的数字 1 的值。
但是一个新的问题就出现了，加入模 q 的过程后，ts ≡ p (mod q) 并不能说明 ts ≡ p。另一方面，ts !≡ p (mod q) 足以说明 ts ≠ p。因此任何满足 ts ≡ p (mod q) 的位移 s，都必须进一步进行测试，来判断 s 是有效位移还是伪命中点。可以通过显示的 T[s+1..s+m] = P[1..m] 来进一步判断，如果 q 足够大，就可以期望伪命中点很少出现，这样就并不需要太多额外检查了。
下面过程中，输入参数为文本T，模式P，基数d（典型值为|∑|），以及素数q：
RABIN-KARP-MATHER(T, P, d, q) n = length[T] m = length[P] h = d^(m-1) mod q p = 0 t[0] = 0 for i = (1 to m) ; 预处理 p = (dp + P[i]) mod q t[0] = (dt[0] + T[i]) mod q for s = (0 to n-m) ; 开始匹配 if (p = t[s]) ; 找到命中点 if P[1..m] = T[s+1..s+m] ; 判断是否为伪命中点 print s if (s < n-m) ; 继续判断后续字符串 then t[s+1] = (d(t[s] - T[s+1]h) + T[s+m+1]) mod q
最后再仔细分析一下该算法运行时间：
在实际应用中，有效位移数一般很少，因此期望匹配时间为 O(n+m)，再加上处理伪命中点的时间。假定 q 是从适当大的整数中随机选出，可以得出未命中次数为 O(n/q)，同时，对于每次命中测试时间代价为 O(m)，因此Rabin-Karp算法期望运行时间为 O(n) + O(m(v+n/q))。其中 v 是有效位移个数。如果 q ≥ m 且 v = O(1)，则这一算法运行时间为 O(n)，即如果有效位移数很少，且素数 q 比模式 P 的长度大得多，则可以预计Rabin-Karp算法匹配时间为 O(n+m)。
利用有限自动机进行字符串匹配
用于字符串匹配的自动机是非常有效的：他们只对每个文本字符检查一次，并且检查每个文本字符的时间为常数。因此建立好自动机后需要时间为 O(n)。但是如果字符全集 ∑ 很大，建立自动机也需要消耗很多时间，后面会讨论如何减少建立自动机时间的方法。
有限自动机
一个有限自动机 M 是一个5元组 (Q, q0, A, ∑, δ)：
Q 是状态的有限集合；
q0∈Q 是初始状态；
A⊆Q 是一个接受状态集合；
∑ 是有限的输入字母表；
δ 是一个 Q × ∑ 到 Q 的函数，称为 M 的转移函数。
有限自动机开始于状态q0，每次读入输入字符串的一个字符。如果 M 在状态 q 时读入了字符 a，则他从状态 q 变为状态 δ(q, a)。每当其当前状态 q 属于 A 时，就说 M 接受了迄今为止所读入的字符串。没有被接受的输入称为被拒绝的输入。
如左图一个简单的两状态自动机 M，状态集 Q = {0, 1}，初始状态 q0 = 0，输入字母表 ∑ = {a, b}。
转移函数 δ 如左表。右图为等价状态转换图，状态 1 是仅有的接受状态，有向边表示转移。
此状态机只接受那些“具有奇数个 a 字符的字符串”。
例如，对于输入字符串 x = {a, b, a, a, a}，此状态机状态序列（包括初始状态）为 <0, 1, 0, 1, 0, 1>，因而接受该输入。
对于输入字符串 x' = {a, b, b, a, a}，状态序列为 <0, 1, 0, 0, 1, 0>，因而拒绝该收入。
除此之外我们还定义一个终态函数φ，是从∑* 到 Q 的映射。对于 φ(w) 表示自动机读取完字符串 w 后的终止状态，因此只有 φ(w)∈A 时，自动机 M 才接受该字符串。可以用如下递归关系定义终态函数：
φ(ɛ) = q0
φ(wa) = δ(φ(w), a) , (w∈∑*, a ∈∑)
构造字符串匹配自动机
对每个模式串 P 而言，都有一个相应的一个匹配自动机。如图给出了一个模式 P = ababaca 的自动机构造过程：
为了构造一个自动机，我们应当首先定义一个辅助函数σ，称为相应模式串 P[1..m] 的后缀函数。函数 σ 是一个从 ∑* 到 {0, 1, 2, ..., m} 上定义的映射。σ(x)表示文本串 x 的后缀的长度，且该后缀是模式串 P 的最长前缀。
即 σ(x) = max{k : Pk ⊐ x}。例如，对于模式串 P = ab，有 σ(ɛ) = 0, σ(ccaca) = 1, σ(ccab) = 2。对于一个长度为 m 的模式串 P 而言，当且仅当 P ⊐ x 时，σ(x) = m。根据后缀函数的定义有：x ⊐ y，则 σ(x) ≤ σ(y)。
所以，对于给定模式串 P[1..m]，对应字符串匹配自动机定义如下：
状态集 Q = {0, 1, ..., m}，初始状态 q0 = 0，接受状态 A = {m}；
对任意状态 q 和字符 a，变迁函数 δ 定义为：δ(q, a) = σ(Pqa)。
我们之所以有 δ(q, a) = σ(Pqa)，是为了追踪当前已匹配最长的模式串 P 的前缀。考虑当前读取的最后一个字符 T[i]，为了寻找文本串 T 的一个子字符串可以匹配模式串 P 的前缀 Pj，Pj 一定是 T[i] 的后缀。
假设状态 q 是读取 T[i] 后的状态，即 q = φ(T[i])。因为我们有变迁函数δ，所以当其状态 q 能够告诉我们匹配 T[i] 后缀的P的最长前缀的长度，即在状态 q 下，Pq ⊐ Ti 且 q = σ(Ti)。
所以当 q = m 时，便可以知道匹配成功。因为 φ(Ti) 和 σ(Ti) 都等于 q，所以自动机运行时能够保持如下不变式：φ(Ti) = σ(Ti)。
todo
KMP算法
大名鼎鼎的KMP算法事实上不如自动机算法复杂。KMP算法效率很高，主要是避免了两个问题：第一，避免了朴素算法中大量无谓的移动和对比信息的浪费；第二，避免了自动机算法中构造自动机消耗大量的时间。
todo
