1143.最长公共子序列
1143.最长公共子序列
题目
给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。
一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1：
输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace" ，它的长度为 3 。
示例 2：
输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。
示例 3：
输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。
提示：
1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-common-subsequence
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
题解
这道题可以看成718.最长重复子数组和300.最长递增子序列的结合版本。
dp数组及其下标的含义
我们首先按照718的思路设置状态
dp[i][j]表示[0，i-1]的字符串和[0.j-1]的字符串中公共的、长度最长的子序列长度。
dp[i][j]如何推出？
如果text1.charAt(i-1) == text2.charAt(j-1),则dp[i][j] = dp[i-1][j-1] + 1
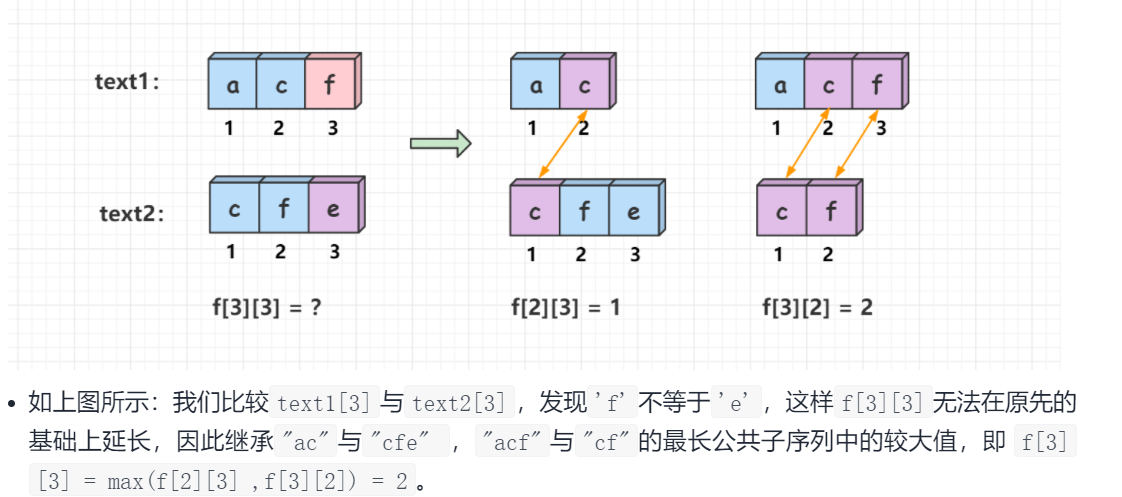
如果text1.charAt(i-1) ≠ text2.charAt(j-1)，两个字符串的最后一位不相等，那么字符串text1的[0,i-1]区间和字符串text2的[0,j-1]区间的最长公共子序列长度无法延长，因此dp[i][j]就会继承dp[i-1][j]与dp[i][j-1]中的较大值，dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j])
这里思考还是得围绕递推式主旨如何到这一步？选择哪种走法？
因为有两种路径可以到这一步，一个是text1的[0,i-2]text2的[0,j-1]，i在走一步；一个是text1的[0,i-1]text2的[0,j-2]，j在走一步。
图源于题解,这里开始我也想不通为什么取两者最大值，举例子感觉更容易理解一下
代码
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int len1=text1.length();
int len2=text2.length();
int dp[][] = new int[len1+1][len2+1];
dp[1][1] = (text1.charAt(0) == text2.charAt(0))?1:0;
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
if(text1.charAt(i-1) == text2.charAt(j-1))
dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);
}
}
return dp[len1][len2];
}
}
