213.打家劫舍Ⅱ
213.打家劫舍Ⅱ
题目
你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。
示例 1：
输入：nums = [2,3,2]
输出：3
解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。
示例 2：
输入：nums = [1,2,3,1]
输出：4
解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 3：
输入：nums = [0]
输出：0
提示：
1 <= nums.length <= 100
0 <= nums[i] <= 1000
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/house-robber-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
题解
动态规划中每一个状态一定是由上一个状态推导出来的。动态规划是由上一个结果推出这一次的结果，往往对具体的东西有忽略。
1.确定dp数组及下标的含义
从昨天的学习中，发现这里可以从定义子问题入手。
本题的问题是：偷完所有(n)的房子，最大金额f(n)是多少?
现在将规模变小，描述子问题，那么就是偷完k个房子，最大金额f(n)是多少？
dp[i]:考虑下标为i(包含)个房子或者说偷完前i(包含)个房子，最大金额为dp[i]
2.确定递推式
dp[i]如何推出？
这道题与之前那道的区别就是，房子是一个圈。
那么可以从已知推未知，去掉头或者去掉尾就和之前的一样了。 --> 环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃，因此可以把此环状排列房间问题约化为两个单排排列房间子问题：
成环问题小技巧★★★★★:很多成环问题都可以拿出来头跟尾分别讨论
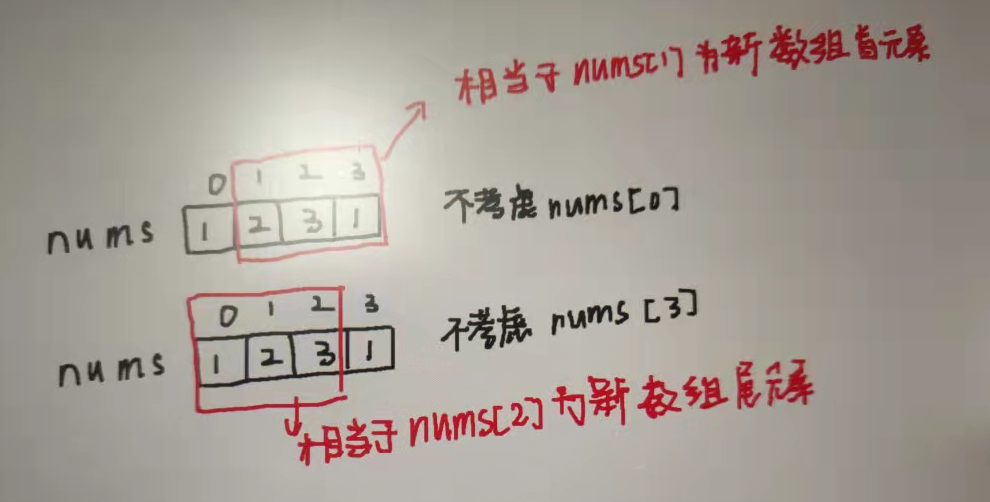
如图所示，相当于去掉头元素或去掉尾元素，因为头尾元素肯定是不能共存，只能选择其中一个或者都不选，这样剩下的数组就是之前198一样了，使用198的解即可。
- 如果i的房间选择偷，那么考虑i-2以内的房间，dp[i] = dp[i-2]+nums[i]
- 如果i的房间选择不偷，那么考虑i-1以内的房间，dp[i] = dp[i-1]
那么dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1])
技巧：使用双指针来控制数组区间选择（产生新数组）
把该部分抽离出来
/*
返回的是一个int类型，表示新数组的最大偷盗金额。
参数：两个指针控制新数组的区间，nums数组本身
*/
int robBasic(int start,int end,int [] nums){
//如果只有一个元素，直接返回
int len = end - start + 1;
if(len == 1) return nums[start];
int [] dp =new int dp[len];
//dp数组
dp[0] = nums[start];
dp[1] = Math.max(dp[0],nums[start+1]);
for(int i=2;i<len;i++){
dp[i] = Math.max(dp[i-2]+nums[start+i],dp[i-1]);
}
return dp[end];
}
空间优化
dp[i]只与dp[i-1]与dp[i-2]有关，只与前两个元素有关，那么我们使用两个变量来代替。
/*
返回的是一个int类型，表示新数组的最大偷盗金额。
参数：两个指针控制新数组的区间，nums数组本身
*/
int robBasic(int start,int end,int [] nums){
//如果只有一个元素，直接返回
int len = end - start + 1;
if(len == 1) return nums[start];
//两个变量来代替
//int [] dp =new int dp[len];
int pre=0; //前两个
int cur=0; //前一个
//执行len次
for(int i=0;i<len;i++){
int temp = Math.max(cur,pre+nums[start+i]); //当前
pre = cur;
cur = temp;
}
return cur;
}
代码
class Solution {
public int rob(int[] nums) {
int len = nums.length;
if(len == 1) return nums[0];
return Math.max(robBasic(1,len-1,nums),robBasic(0,len-2,nums));
}
int robBasic(int start,int end,int [] nums){
int len = end - start + 1;
if(len == 1) return nums[start];
int pre=0;
int cur=0;
int temp;
for(int i=0;i<len;i++){
temp = Math.max(cur,pre+nums[start+i]);
pre = cur;
cur = temp;
}
return cur;
}
}
