122. 买卖股票的最佳时机 II
122. 买卖股票的最佳时机 II
题目
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题解1-贪心法
局部最优解:每次买卖都要赚钱。全局最优解:获得的利润最大。
一天不能同时买和卖,那么至少两天为一个单位。这里比较重要的是意识到分解的想法。

注释:这里看起来第二天第三天第四天是同时买入和卖出,其实不是这样的。这里只是将prices[4]-prices[1]分解成了prices[4]-prices[3]+prices[3]-prices[2]+prices[2]-prices[i]
这样拆了之后可以把相隔多天的买卖转换成相邻两天做计算,那么只要相邻的利润为正就可以加入总利润之中。
直接说分解的思想其实难以一下子想到。
数组中元素差相关的题,用画图的办法更容易理解。
每次买卖都要赚钱,那么就选择递增的子序列。
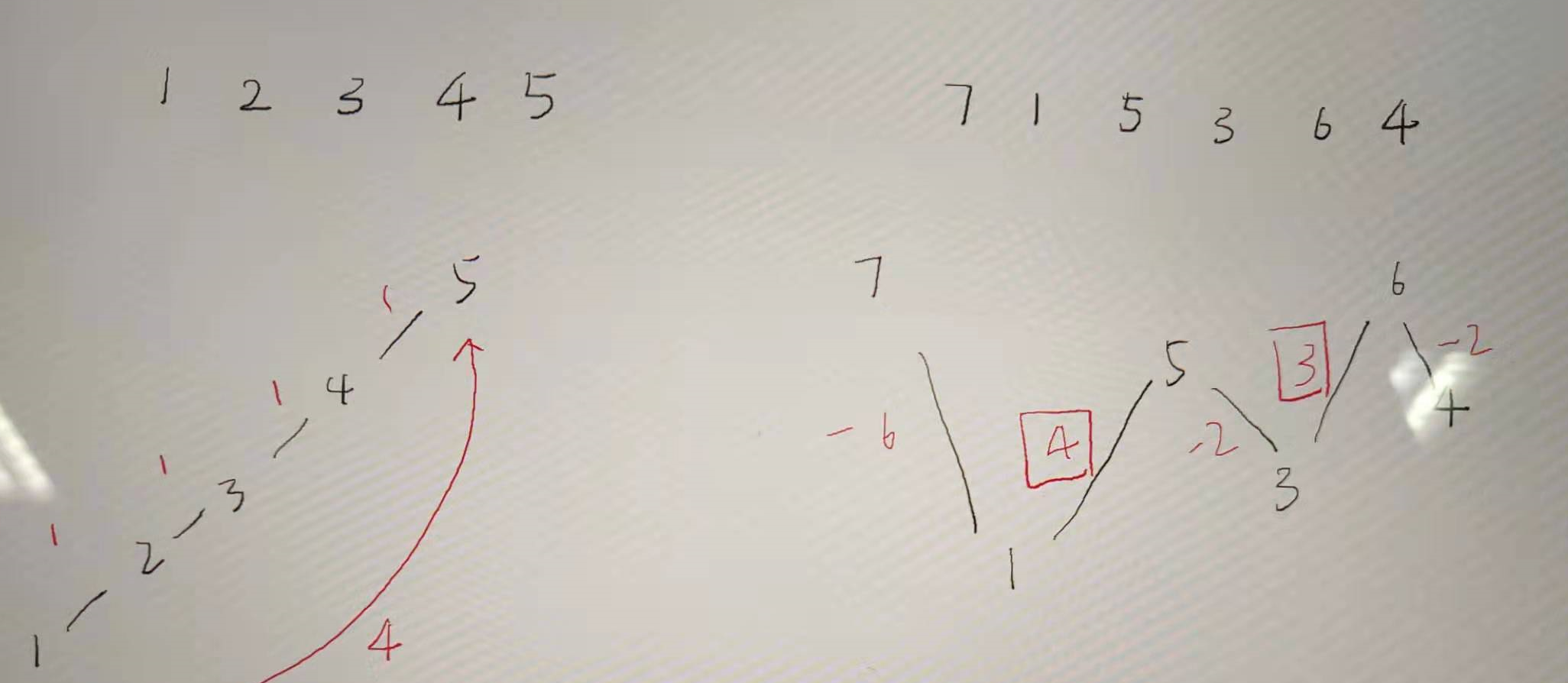
可以很明显的看出来选择两天买卖利润为正的,即使是路径1-2、2-3、3-4、4-5,也可以选择另外一条路1-5达到一样的结果
代码
class Solution {
public int maxProfit(int[] prices) {
int maxprofit = 0;
int len = prices.length;
if(len==1) return maxprofit;
for(int i =len-1;i>0;i--){
int profit = prices[i]-prices[i-1];
if(profit>0) maxprofit+=profit;
}
return maxprofit;
}
}
题解2-动态规划
这道题与121.买卖股票的最佳时机不同的是是可以多次买卖。
题目只问最大利润,没有问这几天具体哪一天买、哪一天卖,因此可以考虑使用 动态规划 的方法来解决。
- 动态规划用于求解 多阶段决策问题 ;
- 动态规划问题的问法:只问最优解,不问具体的解;
每一天还是只有两种状态:持有与不持有。
dp[i][0]:表示第i天持有状态下的最大利润
dp[i][1]:表示第i天不持有状态下的最大利润
如果第i天是持有状态
- 如果之前就是持有状态,那么dp[i][0] = dp[i-1][0]
- 如果之前是不持有状态,那么dp[i][0] = dp[i-1][1] - prices[i],这里与之前不同是因为之前可能已经交易了几次有利润。
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]-prices[i])
如果第i天是不持有状态
- 如果之前就是不持有状态,那么dp[i][1] = dp[i-1][1]
- 如果之前是持有状态,那今天是卖出操作。dp[i][1] = dp[i-1][0] + prices[i]
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i])
这里具有前缀性质,即i用i-1考虑,i-1用i-2考虑,考虑了之前天数的交易
初始化dp数组
dp[0][0] = -prices[0];
dp[0][1] = 0;
空间优化
通过观察递推式,可以看出来当天的两种状态,只与前一天的两种状态有关,所以我们使用两个变量来表示当天的持有状态on和不持有状态off
在两个递推式中,持有状态和不持有状态是互相依赖关系,所以需要用变量来存储上一次的结果,避免本次覆盖上一次的结果后影响结果。
最后一天肯定是不持有时利润更高,所以返回off
//dp[0][0] = -prices[0];
//dp[0][1] = 0;
int on = -prices[0];
int off = 0;
int tempOn=0;
for(int i=1;i<prices.length;i++){
//先保存上一次的状态
tempOn=on;
//dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]-prices[i])
on = Math.max(on,off-prices[i]);
//dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i])
off=Math.max(off,tempOn+prices[i]);
}
代码
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if(len==1)return 0;
int on = -prices[0];
int off = 0;
int tempOn=0;
for(int i=1;i<len;i++){
tempOn=on;
on = Math.max(on,off-prices[i]);
off=Math.max(off,tempOn+prices[i]);
}
return off;
}
}


