37.解数独
37.解数独
题目
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
示例:
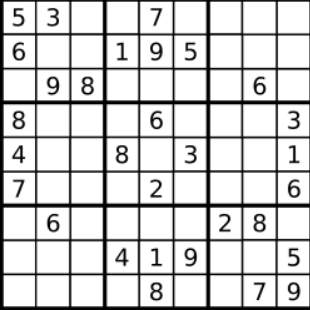
输入:board = [
["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
输出:[
["5","3","4","6","7","8","9","1","2"],
["6","7","2","1","9","5","3","4","8"],
["1","9","8","3","4","2","5","6","7"],
["8","5","9","7","6","1","4","2","3"],
["4","2","6","8","5","3","7","9","1"],
["7","1","3","9","2","4","8","5","6"],
["9","6","1","5","3","7","2","8","4"],
["2","8","7","4","1","9","6","3","5"],
["3","4","5","2","8","6","1","7","9"]
]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/sudoku-solver
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题解
之前递归里的循环都是一次循环,虽然N皇后也是NxN问题,但是每一行每一列只放一个皇后,一层for来遍历一行,递归来遍历列,然后一行一行确定皇后的位置。
数独是每一个位置都要放一个数字,并检查数字是否合法。
本质是枚举,那么也可以使用回溯法。
这里需要考虑的问题也是,如何验证是否在一行一列一个九宫格只出现了一次?依照之前N皇后的思路,采用for循环的办法。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。所以3x3的区间是确定的。
/*
需要知道当前数的位置来选择比较空间
当前数的值用于比较
board用于比较对象
*/
boolean isVal(int x,int y,char num,char[][] board){
for(int i=0;i<9;i++){
//一行进行比较
if(num == board[y][i]) return false;
//比较列
if(num == board[i][x])return false;
}
/*
当x=0,1,2时,比较的是第一块3x3 比较起点是0
当x=3,4,5时,比较的时第二块,起点是3
*/
int startX = (x/3)*3;
int startY = (y/3)*3;
for(int i = startY;i<startY+3;i++){
//如果是本行则不用比较了
if(i==y) continue;
for(int j =startX;j<startX+3;j++){
//如果是本列也不用比较了
if(j==x) continue;
if(board[i][j]==num) return false;
}
}
return true;
}
递归的参数和返回值
这道题是需要返回值的,找到一种解就直接返回,不需要再去找其他的解了。
参数:
char[][] board:输入
backtracing(char[][] board);
递归单层逻辑
需要两层循环,外层循环代表行数,内层循环代表列数。取值是需要遍历整个空间的。
boolean backtracing(char[][] board){
for(int y=0;y<9;y++){
for(int x=0;x<9;x++){//board[y][x]代表当前数
if(board[y][x]!='.')continue;// 当前树已有默认值,不需要再去取值了
for(char num='0';num<'10';num++){ //开始取值,范围从0到9
if(isVal(x,y,num,board)){
board[y][x]=num; //取值
if(backtracing(board)) return true; //如果找到一种正确的情况立即返回。 这里进行了递归操作
board[y][x]='.';//回溯
}
}
//9个数都取完了还不行,说明有错,那么就回溯往前找
return false;
}
}
//没有false说明是正确的则返回true,这里包含了递归终止条件
return true;
}
因为递归函数是有返回值的,所以可以利用递归函数的返回值来控制递归的结束。
代码
class Solution {
public void solveSudoku(char[][] board) {
backtracing(board);
}
boolean backtracing(char[][] board){
for(int y=0;y<9;y++){
for(int x=0;x<9;x++){
if(board[y][x]!='.')continue;
for(char num='1';num<='9';num++){
if(isVal(x,y,num,board)){
board[y][x]=num;
if(backtracing(board)) return true;
board[y][x]='.';
}
}
return false;
}
}
return true;
}
boolean isVal(int x,int y,char num,char[][] board){
for(int i=0;i<9;i++){
if(num == board[y][i] ||num == board[i][x]) return false;
}
int startX = (x/3)*3;
int startY = (y/3)*3;
for(int i = startY;i<startY+3;i++){
if(i==y) continue;
for(int j =startX;j<startX+3;j++){
if(j==x) continue;
if(board[i][j]==num) return false;
}
}
return true;
}
}
题解2
阅读了别的题解,感觉这种办法逻辑更清晰容易理解,所以记录下来。
需要声明布尔数组,表明行列3x3中某个数字是否被使用了,被使用了为true,没有被使用false。
先初始化布尔数组
//[row][num] 第一个代表行号/列号/块号,第二个代表哪个数被使用过了1对应索引0,2对应索引1..
boolean[][] row = new boolean[9][9];
boolean[][] col = new boolean[9][9];
boolean[][] box = new boolean[9][9];
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] == '.') continue;
int num = board[i][j] - '1';
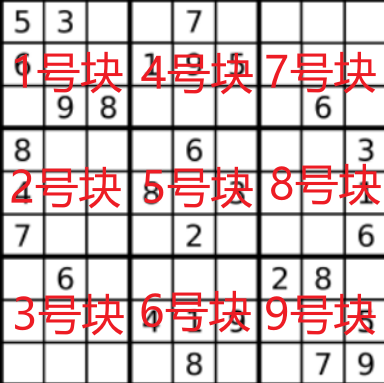
int k = (i / 3) * 3 + j / 3; //块号
row[i][num] = col[j][num] = box[k][num] = true;
}
}
这里块号的处理感觉非常精彩! int k = (i / 3) * 3 + j / 3;
主要的思路是一块一块去枚举。找到一条可行的就行,所以需要及时返回。
boolean backtracing(char[][] board, int n, boolean[][] row, boolean[][] col, boolean[][] box) {
if (n == 81) return true; //n用于记录格子数,从0开始
int i = n / 9, j = n % 9;//i表示行号、j表示列号
//情况1不需要填充
/*
这里要return的原因,递归只看当前块,这里是不需要填充的。当前块返回的结果=后面块返回的结果+当前块(true)
如果后面返回false,那么当前结果向前面返回也是false
*/
if (board[i][j] != '.') return backtracing(board, n + 1, row, col, box);
//情况2需要填充
int k = (i / 3) * 3 + j / 3; //k表示块号
for(int num=0;num<9;num++){ //从0开始对应数组的索引值
if(row[i][num] || col[j][num] || box[k][num]) continue; //如果有一个存在就说明当前数不行,去找下一个数
//这说明当前数可以,处理当前数
board[i][j] = (char) (num + '1');
row[i][num] = col[j][num] = box[k][num] = true;
if (backtracing(board, n + 1, row, col, box)) return true; //如果下一个返回true,当前的也填好了就直接返回true 这里用if来判断而不是直接用return是因为直接return后面的回溯代码不会被执行。
board[i][j] = '.';
row[i][num] = col[j][num] = box[k][num] = false;//回溯
}
//9个数找完了都没有合适的
return false;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号