51.N皇后问题

51.N皇后问题

题目

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1

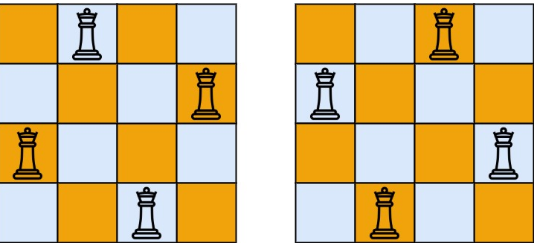
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9
• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/n-queens
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

N皇后问题可以看出本质也是枚举出所有可能选择一种符合条件的，所以采取回溯法。

图太难画了，在网上找了一张。当n=4的时候

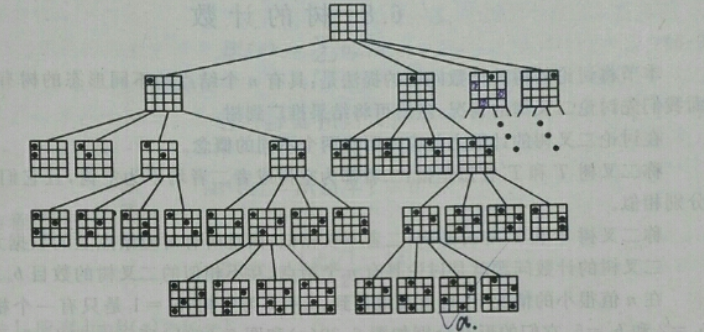
递归的层数和循环次数都等于n

这里有个问题，如何判断是否在一条纵行上或在一条斜线上?
可以把棋盘看成二维数组[x,y],递归的层数就是x，for循环就是y

isVal(x,y,board){
//在一条纵行上
for(int i=0;i<y;i++){
	if(board[i][x]=='Q') return false;
}
//在右斜线上
for(int i = y-1,j=x+1;i>=0&&j<=board.length-1;i--,j++){
	if(board[i][j]=='Q') return false;
}

//在左斜线上
for(int i = y-1,j=x-1;i>=0&&j>=0;i--,j--){
	if(board[i][j]=='Q') return false;
	}
return true;
}

递归三部曲

y:表示当前递归的层数
char[][] board：表示棋盘的状态
int n:递归终止的时候会用上

List<List<String>> res  = new ArrayList<>();
char [] [] board = new char [n] [n]; //这里使用的是二维数组,最后还需要转换成List<String>
void backtracing(int y,char[] [] path,int n)

递归的终止条件
递归的终止条件是path的长度等于n，但是这里使用二维数组初始化时就设置了长度所以不能使用这种判断条件。
y表示递归的层数，当y==n时说明到了叶子节点。

if(y==n){
//Array2List将二维数组转换成List<String>
res.add(Array2List(board))
return;
}

String与char[]之间的转换
String -> char[]
str.toCharArray() 返回一个char类型的数组
char[] -> String 调用String的构造器
new String(arr) 返回一个String

Array2List将二维数组转换成List<String>

List<String> Array2List(char[][] arr){
	 List<String> list = new ArrayList<>();
      for(char[] s : arr){
		//['a','b','c']转换成"abc"
		 list.add(new String(s));
		 return list;
      }
}

单层递归的逻辑

for每一层都是从0-n-1中进行选择，并且代表棋盘的x位置。
如果是合法取值，则改为该位置为Q。

for(int x=0;x<n;x++){
	if(y<=0 || !isVal(x,y,board)) continue; //第一排是不需要验证的
	board[y][x] = 'Q';
	backtracing(y+1,board,n);
	board[y][x] = '.';
}

代码

class Solution {
    List<List<String>> res  = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        char [] [] board = new char [n] [n];
         for(int i=0;i<n;i++){
          Arrays.fill(board[i],'.'); //先全部填充.
        }
        backtracing(0,board,n);
        return res;
    }
	//递归函数
    void backtracing(int y,char[] [] board,int n){
        if(y==n){
            res.add(Array2List(board));
            return;
        }
        for(int x=0;x<n;x++){
            if(y>0 && !isVal(x,y,board))continue;
    	    board[y][x] = 'Q';
	        backtracing(y+1,board,n);
	        board[y][x] = '.';
            }
        }
		//判断是否合法
    boolean isVal(int x,int y,char[][] board){
        for(int i=0;i<y;i++){ //在一条线上
        	if(board[i][x]=='Q') return false;
        }

        for(int i = y-1,j=x+1;i>=0&&j<=board.length-1;i--,j++){//检查右上角
	        if(board[i][j]=='Q') return false;
        }
		//检查左上角
        for(int i = y-1,j=x-1;i>=0&&j>=0;i--,j--){
    	    if(board[i][j]=='Q') return false;
        }
        return true;
    }
	//二维char数组转换成 List<String>
    List<String> Array2List(char[][] arr){
	  List<String> list = new ArrayList<>();
      for(char[] s : arr){
          list.add(new String(s));
      }
      return list;
    }
}