47.全排列Ⅱ

47.全排列Ⅱ

题目

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：
输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/permutations-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

输入的nums是可以包含重复数字的，对排列之后的结果要求是不重复的。

之前处理输入包含重复，输出不重复的思路是:对输入数组排序是为了方便剪枝掉重复的结果。

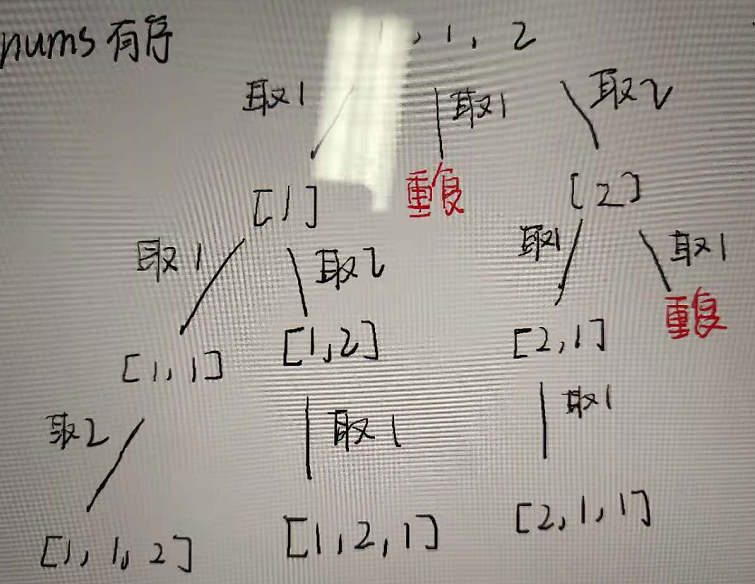
通过分别画出nums无序与有序的图，发现树的同一层仍然是不能重复取相同值的，那么还是需要对输入数组进行排序，通过比较前后取值是否一样来判断是否取值重复。

对于每一个分支path来说，因为每一次循环都是从nums[0]取到最后，那么已经取过的位置不能再取了。
46题我们使用的是path的路径之中有就说明已经取值了，没有就说明还没有取过值。但这道题nums是可以有值重复的元素，所以设置一个visited数组记录元素是否被访问过。

递归的参数和返回值

List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
void backtracing(int [] nums);

回溯的终止条件

全排序是对nums的元素进行排序，那么排序完path的长度应该等于nums的长度。

if(path.size() == nums.length){
	res.add(new ArrayList(path));
	return;
}

递归的单层逻辑

这里关于哪些值不可以我其实有点不清楚。重新把抽象树补充具体了。

同一分支的相同值情况
visited[i-1]==1&&nums[i]==nums[i-1]说明1#取值的时候1已经取了，那么当前情况是1#与1在同一分支上，这种情况是允许的。
同一层相同值的情况
visited[i]==0&&nums[i]==nums[i-1]说明当前分支1是没取的，1#与1是在同一层的情况，这种情况是不允许的。

for(int i=0;i<nums.length;i++){
     if(visited[i]==1) continue; //一个分支上的每个位置只能取1次
     if(i>0&&visited[i-1]==0&&nums[i]==nums[i-1])continue;
     visited[i]=1;
     path.add(nums[i]);
     backtracing(nums,visited);
     visited[i]=0;
     path.remove(path.size()-1);
   }

代码

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    List<Integer> path;
    public List<List<Integer>> permuteUnique(int[] nums) {
        if(nums.length==0) return res;
        path = new ArrayList<>();
		//如果该数组只有的取值只有0或1 可以考虑用boolean[] visited = new boolean[nums.length];
        int [] visited = new int [nums.length];
        Arrays.sort(nums);
        backtracing(nums,visited);
        return res;
    }
    void backtracing(int[] nums,int[]visited){
        if(path.size() == nums.length){
        	res.add(new ArrayList(path));
	        return;
        }
        for(int i=0;i<nums.length;i++){
            if(visited[i]==1) continue;
            if(i>0&&visited[i-1]==0&&nums[i]==nums[i-1])continue;
            visited[i]=1;
            path.add(nums[i]);
            backtracing(nums,visited);
            visited[i]=0;
            path.remove(path.size()-1);
        }
    }
}

扩展

阅读了大佬的题解,补充一种新思路

对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高

树层上去重

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) { 
    continue;
}

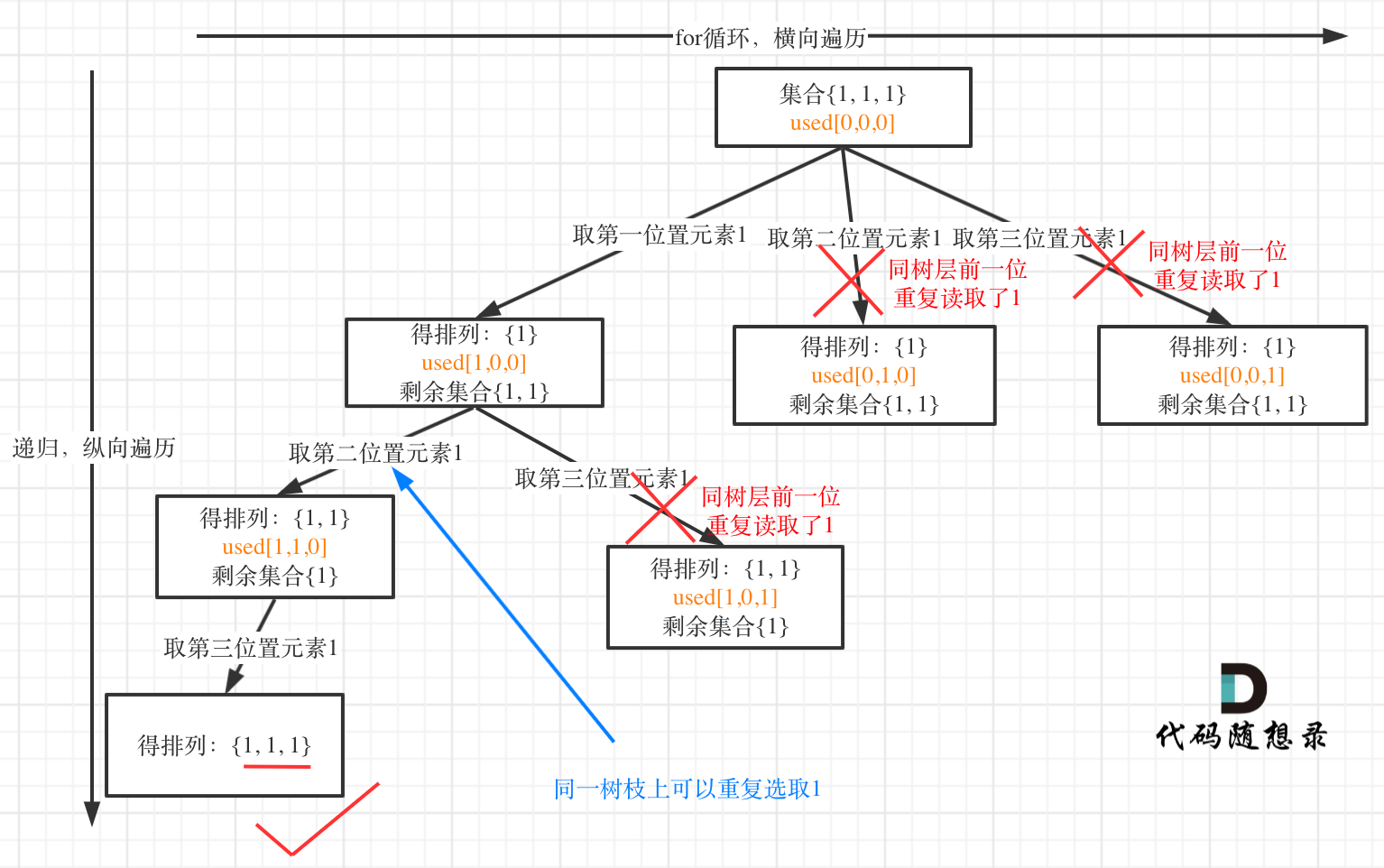
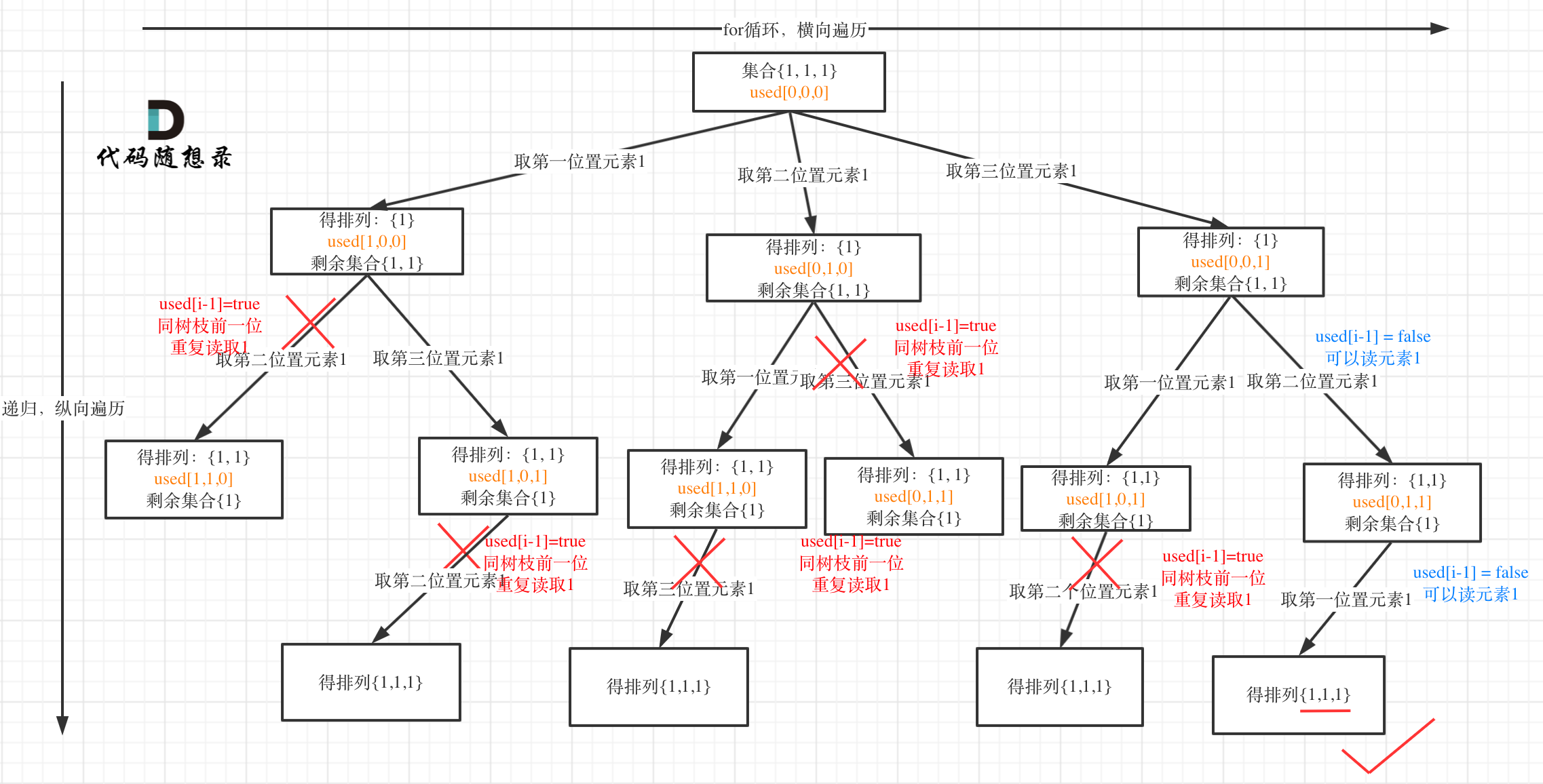
数枝上去重

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) { 
    continue;
}