491.递增子序列

491.递增子序列

题目

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是 2 。

示例：

输入：[4, 6, 7, 7]
输出：[[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

提示：

给定数组的长度不会超过15。
数组中的整数范围是 [-100,100]。
给定数组中可能包含重复数字，相等的数

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/increasing-subsequences
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

思路

题目说的找到所有该数组的递增子序列,这里找的是子序列,其实我不太理解子序列这种具体的说法。
试了两个示例之后，感觉是序列是有序的？然后子序列元素的前后顺序和之前的数组里元素的前后顺序是一致的。

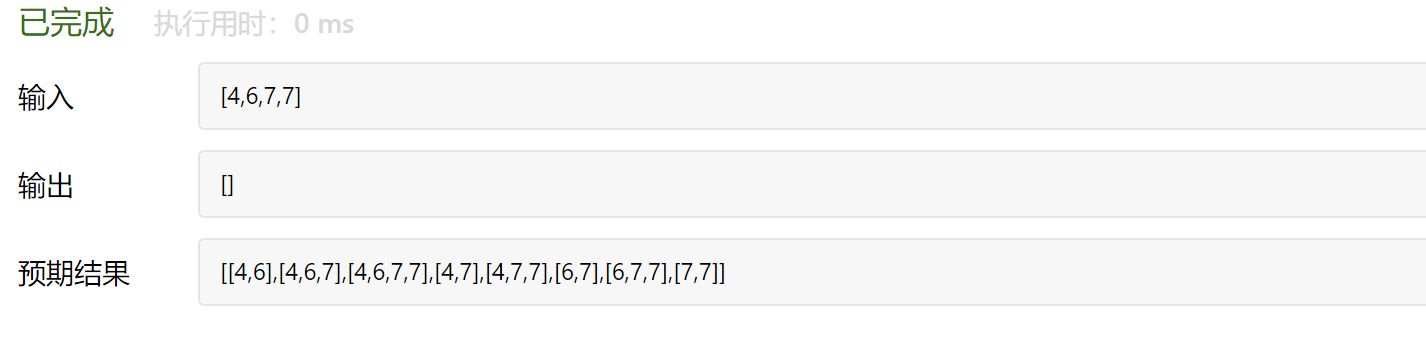
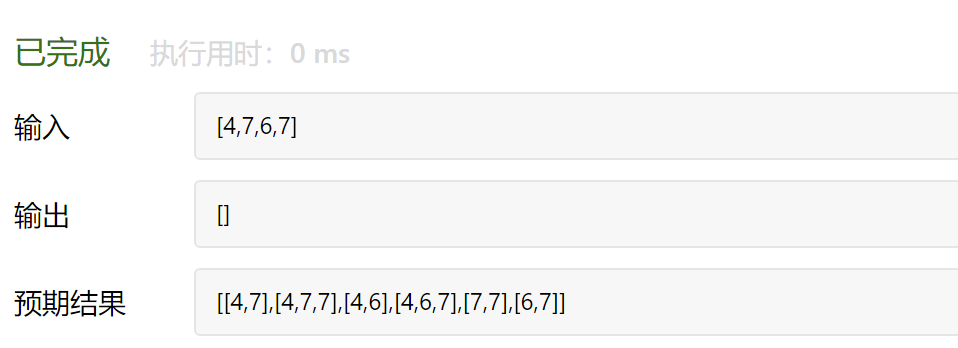
可以发现[4,7,6,7]和[4,6,7,7]的答案是不一样的，那么90题先对原数组排序再去重的思路是没办法用的。

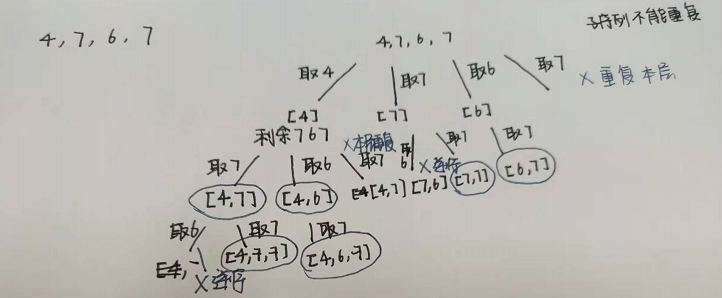
按照之前做题的思路，有两个办法判断是否重复
第一个用hash表，第二个是这道题给正数的范围，那么可以使用数组长度为200的数组arr代表[-100,100]。
如果当前元素是5，那么arr[5+100] = 1

题解

递归的参数和返回值

数组中的元素不能重复取值，那么还是需要startIndex来标识取值区间。

List<List<Integer>> res = new ArrayList<>();
List<Integer> path;
void backtracing(int [] nums,int startIndex);

递归的终止条件

if(startIndex == nums.length)return; //和之前的题一样可以省略

单层递归逻辑

首先先判断当前的元素是否之前已经取过，如果取过了，则跳过。
如果没取过,判断当前元素是否比path路径的最后一个元素大，如果大取值并且加入path,否则跳过当前值。
去重是同一个父节点下的本层去重，所以设置的数组放在单层搜索逻辑中，每一层同父节点的所有节点公用一个数组。

int [] arr =  new int[201]//仅供本层使用，每次向下走的时候先为这层新建一个分支
for(int i = startIndex;i<nums.length;i++){//横向遍历
  	if(path.size()>=2) res.add(new ArrayList(path));
    if(arr[nums[i]+100]==1) continue; //判断是否已经取值避免本层重复取值
	  if( path.size()>0 && nums[i] < path.get( path.size()-1))continue; //这是当前元素比path之前的最后一个元素小，pLen>0里面有数可以比较。
	  //这下面都是符合条件的了
	   arr[nums[i]+100]=1; //这是符合条件设置为1，不符合条件是肯定不是进来的
       path.add(nums[i]);
       backtracing(nums,i+1);
       path.remove(path.size()-1); //这里的回溯是为了取下一个分支，因为不符合条件的并不会进来
}

代码

class Solution {
    List<List<Integer>> res;
    List<Integer> path;
    
    public List<List<Integer>> findSubsequences(int[] nums) {
        res = new ArrayList<>();
        if(nums.length==0) return res;
        path = new ArrayList<>();
        backtracing(nums,0);
        return res;
    }
    void backtracing(int [] nums,int startIndex){
        if(path.size()>=2) res.add(new ArrayList(path));
        int [] arr =  new int[201];
        for(int i = startIndex;i<nums.length;i++){
            if(arr[nums[i]+100]==1) continue;
            if(path.size()>0 && nums[i] < path.get( path.size()-1))continue;
            path.add(nums[i]);
            arr[nums[i]+100]=1;
            backtracing(nums,i+1);
            path.remove(path.size()-1);
    }
}
}