Pytorch 线性回归问题 总结
线性回归 pytorch实现
1.模拟回归问题,生成训练数据
import torch import torch.nn as nn import numpy as np # Hyper-parameters input_size = 10 output_size = 2 num_epochs = 750 learning_rate = 1e-5 np.random.seed(1) # Toy dataset x_train = np.random.randn(1000,10).astype(np.float32) W = np.random.randint(0,20,size = (10,2)) y_train = (x_train.dot(W)).astype(np.float32) x_train.shape,y_train.shape
2.用梯度下降的方法更新未知参数w1, 用随机数初始化w1
w1 = np.random.randn(10,2)
for epoch in range(num_epochs): #forward pass y_pred = x_train.dot(w1) #compute loss loss = np.square(y_pred - y_train).sum() if (epoch+1) % 10 == 0: print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item())) #backward pass grad_y_pred = 2.0*(y_pred - y_train) grad_w1 = x_train.T.dot(grad_y_pred) w1 -= grad_w1*learning_rate
3.输出结果:
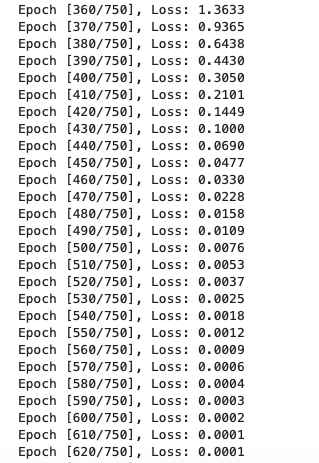
差不多700次左右loss就迭代到0了,我们对比w1和w可以看出它们已经非常接近了。

能否减少迭代次数呢?
我们减少参数量试试:
W是一个10x2的一个矩阵,我们可以分解成W1*W2,W1和W2为10x1,1*2的矩阵这样的话我们的参数从20减少到了12,
减少了将近一半,可能在参数少的时候影响不大,先看看效果。
实现代码:
import torch import torch.nn as nn import numpy as np # Hyper-parameters input_size = 10 output_size = 2 num_epochs = 700 learning_rate = 0.01 np.random.seed(1) # Toy dataset x_train = np.random.randn(1000,10).astype(np.float32) W = np.random.randint(0,20,size = (10,2)) y_train = (x_train.dot(W)).astype(np.float32) x_train.shape,y_train.shape w1 = np.random.randn(10,1) w2 = np.random.randn(1,2) for epoch in range(num_epochs): #forward pass h = x_train.dot(w1) #相当于隐藏层 y_pred = h.dot(w2) #compute loss loss = np.square(y_pred - y_train).sum() if (epoch+1) % 10 == 0: print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item())) #backward pass grad_y_pred = 2.0*(y_pred - y_train) grad_w2 = h.T.dot(grad_y_pred) grad_h = grad_y_pred.dot(w2.T) grad_w1 = x_train.T.dot(grad_h) w1 -= grad_w1*learning_rate w2 -= grad_w2*learning_rate

结果如图,如果学习率太小,loss可能会固定为一个值保持不变,如果学习率较大会产生这种nan的情况。
loss总是不能收敛到0。问题是什么?
我们将刚刚的操作反过来,W1和W2的维度设为10x5,5*2 ,参数量变成了60个比20个多了两倍。
结果很好,loss很快收敛到0,大概在epoch = 420时候就收敛到0,比之前更快

对比W1*W2 和W:
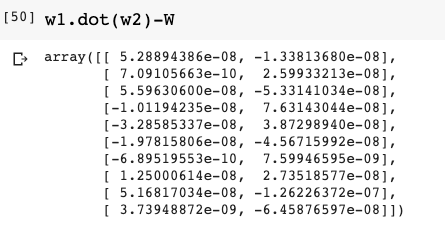
可以看出差距很小,并且综合上面,也可以看出MSE的loss可以很好的反映线性回归拟合的好坏。
如果我们继续增加参数量,会不会让收敛速度更快呢。
会,

迭代次数变少,但是运算时间可能变大了,所以具体问题要具体分析得到合适参数量。
一开始建模的时候,参数越多越好,最后浓缩模型的时候再慢慢调整参数量。
4.用pytorch中的方法实现线性回归
import torch import torch.nn as nn import numpy as np # Hyper-parameters input_size = 10 output_size = 2 num_epochs = 700 learning_rate = 1e-5 torch.manual_seed(1) # Toy dataset x_train = torch.randn(1000,input_size) W = torch.randint(0,20,size = (10,output_size),dtype = torch.float32) y_train = x_train.mm(W) w1 = torch.randn(input_size,5,requires_grad=True) w2 = torch.randn(5,output_size,requires_grad=True) for epoch in range(num_epochs): #forward pass h = x_train.mm(w1) #相当于隐藏层 y_pred = h.mm(w2) #compute loss loss = (y_pred - y_train).pow(2).sum() if (epoch+1) % 10 == 0: print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item())) #backward pass loss.backward() #计算loss对w1 w2的导数 with torch.no_grad(): w1 -= learning_rate*w1.grad w2 -= learning_rate*w2.grad w1.grad.zero_() #清理缓存中的grad w2.grad.zero_()
5.用pytorch中的模型实现线性回归:
import torch import torch.nn as nn import numpy as np # Hyper-parameters input_size = 10 output_size = 2 num_epochs = 700 learning_rate = 1e-5 torch.manual_seed(1) H = 5 # Toy dataset x_train = torch.randn(1000,input_size) W = torch.randint(0,20,size = (10,output_size),dtype = torch.float32) y_train = x_train.mm(W) model = torch.nn.Sequential( torch.nn.Linear(input_size,H,bias=False), torch.nn.Linear(H,output_size,bias=False), ) loss_fn = nn.MSELoss(reduction='sum') for epoch in range(num_epochs): #forward pass y_pred = model(x_train) #compute loss loss = loss_fn(y_pred,y_train) if (epoch+1) % 10 == 0: print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item())) #backward pass model.zero_grad() loss.backward() #计算loss对w1 w2的导数 with torch.no_grad(): for param in model.parameters(): param -= learning_rate*param.grad
'''
也可以用optimizer来做参数更新
'''

6. 利用optim中的优化器来优化参数
import torch import torch.nn as nn import numpy as np # Hyper-parameters input_size = 10 output_size = 2 num_epochs = 700 learning_rate = 1e-1 torch.manual_seed(1) H = 5 # Toy dataset x_train = torch.randn(1000,input_size) W = torch.randint(0,20,size = (10,output_size),dtype = torch.float32) y_train = x_train.mm(W) model = torch.nn.Sequential( torch.nn.Linear(input_size,H,bias=False), torch.nn.Linear(H,output_size,bias=False), ) loss_fn = nn.MSELoss(reduction='sum') optimizer = torch.optim.Adam(model.parameters(),lr = learning_rate) for epoch in range(num_epochs): #forward pass y_pred = model(x_train) #compute loss loss = loss_fn(y_pred,y_train) if (epoch+1) % 10 == 0: print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item())) #backward pass optimizer.zero_grad() loss.backward() #计算loss对w1 w2的导数 #update model parameters optimizer.step()

可以看出用pytorch的模型构建model非常的方便,但是模型内部是已经定义好的,用户只能修改参数,而不能修改模型内部结构。
这需要我们自己定义一个模型:
7. DIY 自己的模型
import torch import torch.nn as nn import numpy as np # Hyper-parameters input_size = 10 output_size = 2 num_epochs = 700 learning_rate = 1e-5 torch.manual_seed(1) H = 5 # Toy dataset x_train = torch.randn(1000,input_size) W = torch.randint(0,20,size = (10,output_size),dtype = torch.float32) y_train = x_train.mm(W) class TwoLayerNet(torch.nn.Module): def __init__(self,input_size,H,output_size): super(TwoLayerNet, self).__init__() self.linear1 = torch.nn.Linear(input_size, H, bias = False) self.linear2 = torch.nn.Linear(H, output_size, bias = False) def forward(self,x): y_pred = self.linear2(self.linear1(x)) return y_pred model = TwoLayerNet(input_size, H, output_size) loss_fn = nn.MSELoss(reduction='sum') optimizer = torch.optim.SGD(model.parameters(),lr = learning_rate) for epoch in range(num_epochs): #forward pass y_pred = model(x_train) #compute loss loss = loss_fn(y_pred,y_train) if (epoch+1) % 10 == 0: print ('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item())) #backward pass optimizer.zero_grad() loss.backward() #计算loss对w1 w2的导数 #update model parameters optimizer.step()
# Save the model checkpoint torch.save(model.state_dict(), 'model.ckpt')
模型参数最后可以保存下来。

