python手写数字识别(从导入数据到导出模型) 总结
python 手写数字识别 (mnist库)#
import numpy as np import pandas as pd import tensorflow as tf from tensorflow.keras import layers import matplotlib.pyplot as plt '''1.打开数据集文件,并且读取mnist数据''' data = np.load('mnist.npy') print(data.files) x_train = data['x_train'] y_train = data['y_train'] x_test = data['x_test'] y_test = data['y_test'] print(x_train.shape)
''' 对数据进行预处理,将图像数据转成四维数据,第一维度为batch_size,第二三维度为图片大小, 第四个维度表示通道数目,mnist数据集为单色灰度图像,所以值为1,如果是彩色则为3。 ''' '''2.数据预处理''' x_train4D = x_train.reshape(x_train.shape[0],28,28,1).astype('float32') #shape[0]表示有多少张图片,即batch_size x_test4D = x_test.reshape(x_test.shape[0],28,28,1).astype('float32') #然后对x数据标准化处理,使取值范围在0,1之间; 对y数据进行One-Hot编码,将0~9映射成一组相同长度的01编码 x_train4D = x_train4D/255 x_test4D = x_test4D/255 y_train01 = tf.keras.utils.to_categorical(y_train) y_test01 = tf.keras.utils.to_categorical(y_test)
'''3.搭建模型''' model = tf.keras.models.Sequential() #选择keras模型库中的线性堆叠模型Sequential() model.add(layers.Conv2D(filters=16, kernel_size=(5,5), padding='same', input_shape=(28,28,1),activation='relu')) model.add(layers.MaxPooling2D(pool_size=(2,2))) #每一层卷积层后面一定要池化,不然起不到降维度的作用,无参数,这一步只是为了浓缩数据 model.add(layers.Conv2D(filters=32, kernel_size=(5,5),padding='same', activation='relu')) #后面层其实可以根据前面层的输出得到input_shape,所以可以不写,但是每一个卷积层都必须写激活函数和padding, # 因为后面层需要知道输出数据的规模shape是多少 model.add(layers.MaxPooling2D(pool_size=(2,2))) # 此时28x28的图片现在只有7x7 model.add(layers.Dropout(0.3)) #使百分之30的神经元失活,避免过拟合 model.add(layers.Flatten()) #转为一维向量输入 model.add(layers.Dense(128,activation='relu')) #后面再加隐藏层,128代表这一层有128个神经元,input_shape依然不用填,Dense()全连接层,只适用于一维数据 #所以前面需要加一个Flatten()层来讲7x7的二维数据转为一维数据输入 model.add(layers.Dropout(0.5)) #卷积层和隐藏层都各需要一个dropout函数来防止过拟合。 model.add(layers.Dense(10, activation='softmax')) #输出层,多分类问题用'softmax'激活函数,二分类问题用'sigmoid'激活函数 print(model.summary())
'''4.训练''' model.compile(loss='categorical_crossentropy',optimizer='adam',metrics=['accuracy']) #交叉熵在多分类问题中常用,可以把细小的概率变化放大,而mse均方差适合拟合回归,不适合分类问题,评估方式这里用的是准确度 train_history = model.fit(x=x_train4D,y=y_train01,validation_split=0.2,epochs=5,batch_size=300,verbose=2) #将百分之20的数据划分为测试数据,每批处理300张图片,verbose = 2显示训练过程 #训练时候需要输入为4维的数据,评价或者预测时候,也需要输入时四维的数据
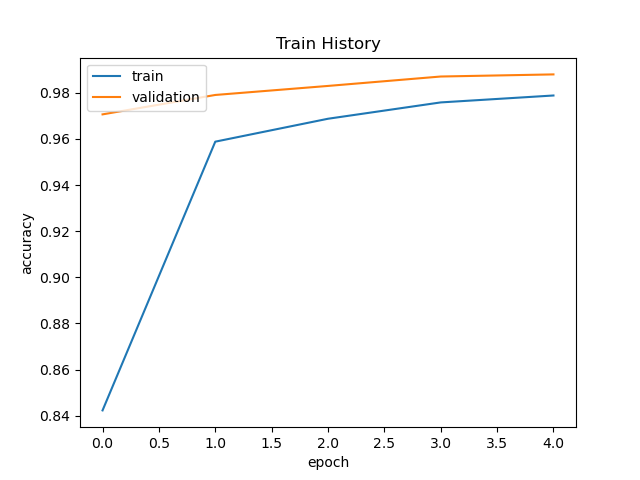
'''5.显示训练结果''' print(train_history.history) #可知里面包含四个组数据,分别是loss, accuracy, val_loss, val_accuracy #自定义一个显示随着迭代次数增加,正确率变化的图表 def show_train_history(train_history, train, validation): plt.plot(train_history.history[train]) # 绘制训练数据的执行结果 plt.plot(train_history.history[validation]) # 绘制验证数据的执行结果 plt.title('Train History') # 图标题 plt.xlabel('epoch') # x轴标签 plt.ylabel('accuracy') # y轴标签 plt.legend(['train', 'validation'], loc='upper left') # 添加左上角图例 show_train_history(train_history, 'accuracy', 'val_accuracy')
'''6.测试'''
#倒数第二步,在测试集上面进行测试
scores = model.evaluate(x_test4D, y_test01)
print('accuracy=', scores[1]) #scores[0] 表示loss值, scores[1]表示正确率
#用模型在测试集上进行预测
prediction = model.predict_classes(x_test4D)
#predict_classes会将预测的One-hot编码转化为一个数值0~9,得到的是一组预测值
#可视化结果
def plot_image_labels_prediction(images, labels, prediction, idx, nums=25):
fig = plt.figure(figsize=(12,14)) # 设置图表大小
if nums > 25: nums = 25 # 最多显示25张图像
for i in range(0, nums):
ax = fig.add_subplot(5, 5, 1 + i) # 子图生成
ax.imshow(images[idx], cmap='binary') # idx是为了方便索引所要查询的图像
title = 'label=' + str(labels[idx]) # 定义title方便图像结果对应
if (len(prediction) > 0): # 如果有预测图像,则显示预测结果
title += ' prediction=' + str(prediction[idx])
ax.set_title(title, fontsize=10) # 设置图像title
ax.set_xticks([]) # 无x刻度
ax.set_yticks([]) # 无y刻度
idx += 1
plt.show()
plot_image_labels_prediction(x_test,y_test,prediction,idx = 400)
下面一行表示的是测试集上的结果,可以看出每次训练相同数据可能得到不同的参数,可能是因为dropout层的原因,
但是准确率都是98%以上,波动不会很大。我们训练相同数据时候准确率达到95%就已经很高了,过高可能会存在过拟合问题。

后面是对结果的评价:(最后保存模型,方便下次再使用该模型)
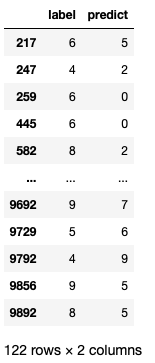
#查找预测错误点 pretb = pd.crosstab(y_test,prediction,rownames=['label'],colnames=['predict']) df = pd.DataFrame({'label':y_test,'predict':prediction}) error = df[df['label']!=df['predict']] print(error)
#最后一步,根据结果调整参数,或者调整网络结构,重复以上操作直到结果满意(前提是模型正确)
可以看到这个模型在测试集上有122个数据预测错误,但是准确度很高,达到98.9%,准确度能否真实的反映模型好坏吗?
我们需要看测试集上数据的分布,因此我们有了下一步:
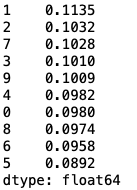
freq = pd.Series(y_test).value_counts()/len(y_test)
print(freq) #得到0~9在测试集上出现的频率,看是否数据不均衡
可以看出数据是十分均衡的。
另外我们继续统计测试集上每个数字出错的频率,看哪一个数字预测错的概率最大。
from scipy.stats import pearsonr,norm
import pandas as pd
import matplotlib.pyplot as plt
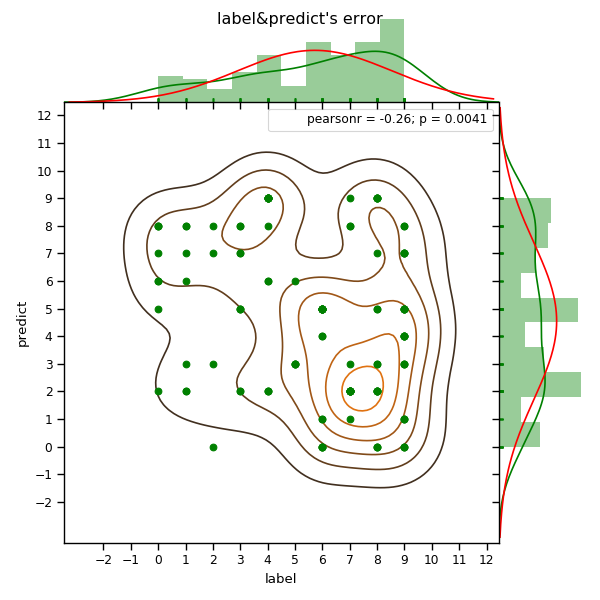
import seaborn as sns data = pd.read_csv('out.csv') print(data) sns.set_context('paper') ax = sns.jointplot('label','predict',data = data,marginal_kws=dict(bins = 10, kde = True, fit = norm, fit_kws = {'color': 'r'}, rug = True),stat_func = pearsonr, space = 0, color = 'g',kind = 'scatter')
#kind = 'scatter', 'reg', 'resid', 'kde', 'hex' ax.plot_joint(sns.kdeplot, zorder = 0, n_levels = 6)#在前面一个图的基础上在加上核密度估计的联合密度分布图,通过plot_joint()实现。 plt.xticks(np.linspace(-2,12,15)) plt.yticks(np.linspace(-2,12,15)) plt.suptitle('label&predict\'s error') plt.show()
可以看出来在标签为7,8,9的数字更容易识别错,
错看成0,1的概率最小,看成其他数字的概率基本一样(见绿色kde曲线)。
我们可以后续在识别7,8,9这三个数字上对模型做进一步优化。
如何导出模型数据呢?
'''7.修改模型或者保存模型便于下次用新数据训练'''
model.save('model.h5') #保存后会在生成一个model.h5文件
from tensorflow.keras.models import load_model model2 = load_model('model.h5') #对测试数据预处理后,再用这个模型进行评价 loss,accuracy = model2.evaluate(x_test4D, y_test01)
# 保存参数,载入参数 model2.save_weights('my_model_weights.h5') model2.load_weights('my_model_weights.h5') # 保存网络结构,载入网络结构 from keras.models import model_from_json json_string = model2.to_json() model2 = model_from_json(json_string) print(json_string) #json_string的值就是该网络的结构,载入的时候只需要调用model_from_json(s) s为字符串可以通过读json文件来得到
标签:
tensorflow2.0
, python


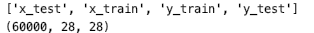






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 终于写完轮子一部分:tcp代理 了,记录一下
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理