Python绘图总结(seaborn库的使用)（下）
上部分介绍了pie以及kdeplot、distplot、jointplot、pairplot的用法分别绘制出数据的饼图、核密度分布图、
柱状图、散点图、以及用jointplot绘制组合图。
下面开始总结（散点图（二维，三维），折线图，（并列，叠加）柱状图，三维曲面图，箱线图的画法）：
（一）散点图：(relplot, scatterplot)
'''
seaborn.relplot(x=None, y=None, hue=None, size=None, style=None, data=None, row=None, col=None, col_wrap=None, row_order=None, col_order=None, palette=None, hue_order=None, hue_norm=None, sizes=None, size_order=None, size_norm=None, markers=None, dashes=None, style_order=None, legend='brief', kind='scatter', height=5, aspect=1, facet_kws=None, **kwargs)
'''
# -*- coding: utf-8 -*-
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import pearsonr,norm
data = pd.read_csv('anscombe.csv')
print(data.head())
sns.set_context('paper')
sns.set_style('ticks',{'font.sans-serif':['simhei','Arial']})
pal = sns.husl_palette(n_colors=4,l = .7)
sns.relplot(x = 'x', y = 'y', data = data, hue = 'dataset',style = 'dataset',sizes = (100,100),palette = pal)
plt.suptitle("不同组的x与y之间的关系")
plt.show()
不同组相同style，都是圆形；
不同组不同style。
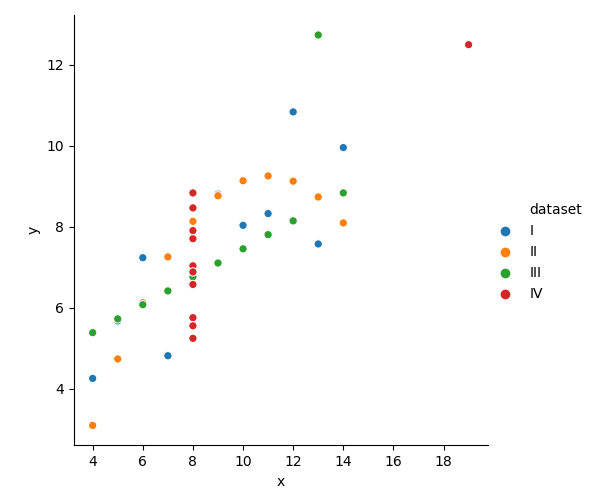
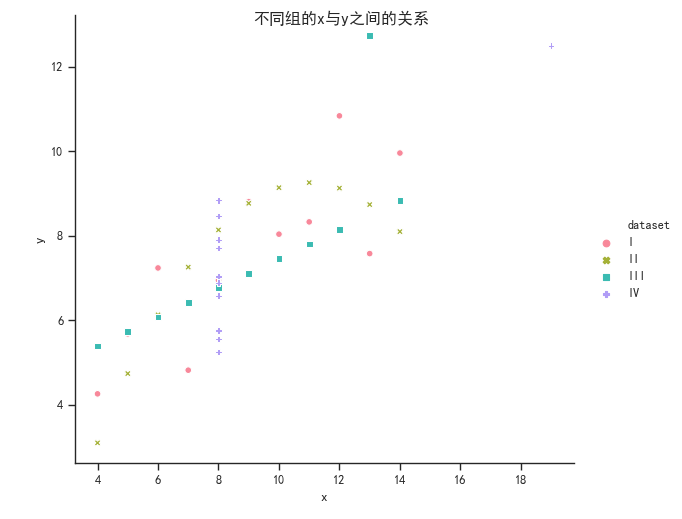
显然我们的目的不仅仅是观察散点分布，更重要的是为了寻求x与y之间以及不同组之间的关系。
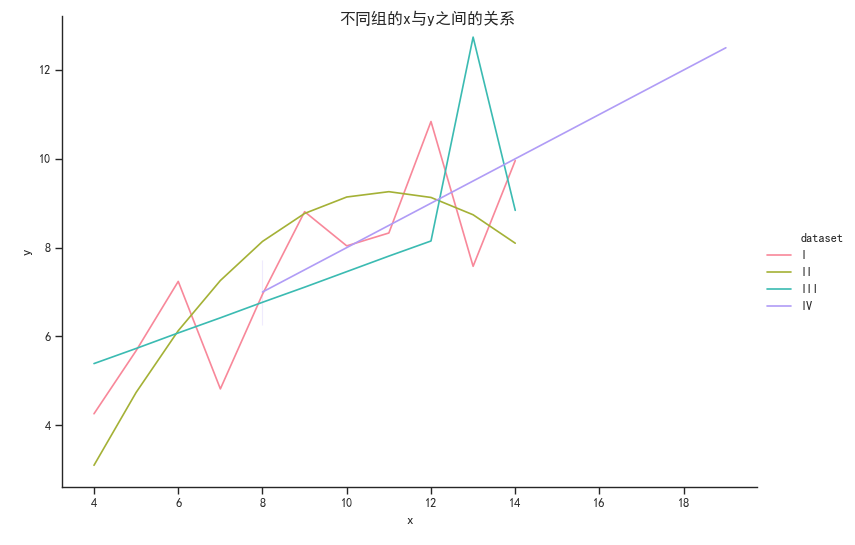
我们对每一组的（x，y）连起来形成一个折线图，仅仅需要将kind = 'scatter'(默认)改为 kind = 'line';
可得图：
可以看出第二组数据点形成的曲线近似于抛物线轨迹，第四组数据点都在直线上（垂直于x的直线，说明y与x无关，因为有一个点偏离较远所以导致折线图出现这种情况），而第一组和第三组，线性不是很明显，但是这两组y与x呈明显的正相关关系。
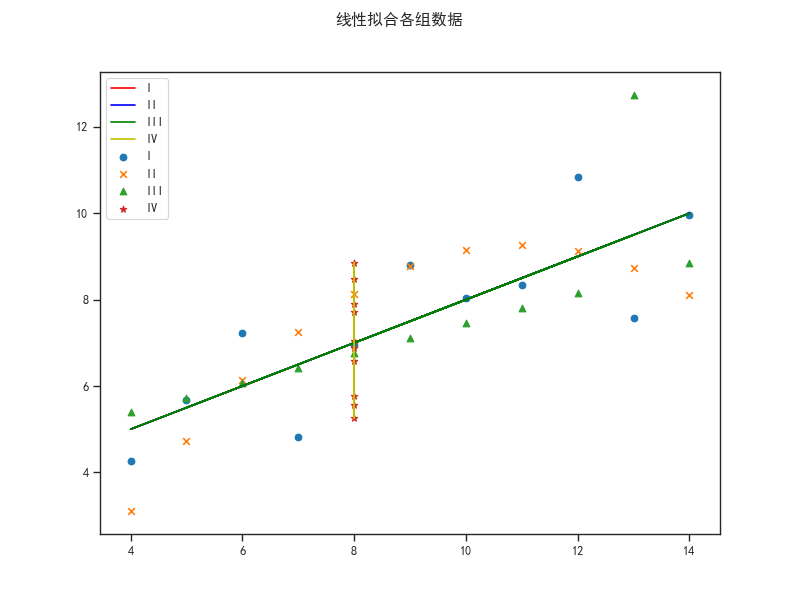
现在我们需要对这几组数据用回归拟合，找出每组内x与y之间的函数关系。
from scipy.stats import linregress data = pd.read_csv('anscombe.csv') print(data.head()) sns.set_context('paper') sns.set_style('ticks',{'font.sans-serif':['simhei','Arial']}) cls = ['I','II','III','IV'] markers = ['o','x','^','*'] c = ['r','b','g','y'] data = data[data['x']<18] #删除异常值，因为我们知道百分之95的数据的x都在（4，18）区间内,离群点对线性回归影响很大，特别是当数据量较小的时候 f = plt.figure(figsize=(8,6)) for i in range(4): dt = data[data['dataset']==cls[i]] k,b,r,p,std = linregress(dt['x'],dt['y']) flag = 1 if np.isnan(k): k,b,r,p,std= linregress(dt['y'],dt['x']) flag = 0 plt.scatter(dt['x'],dt['y'],marker=markers[i],label = cls[i]) if flag: plt.plot(dt['x'],k*dt['x']+b,color = c[i],label = cls[i]) else: plt.plot(k*dt['y']+b,dt['y'],color = c[i],label = cls[i]) flag = 1 plt.legend(loc = 'upper left') plt.suptitle('线性拟合各组数据') plt.show()
箱线图：
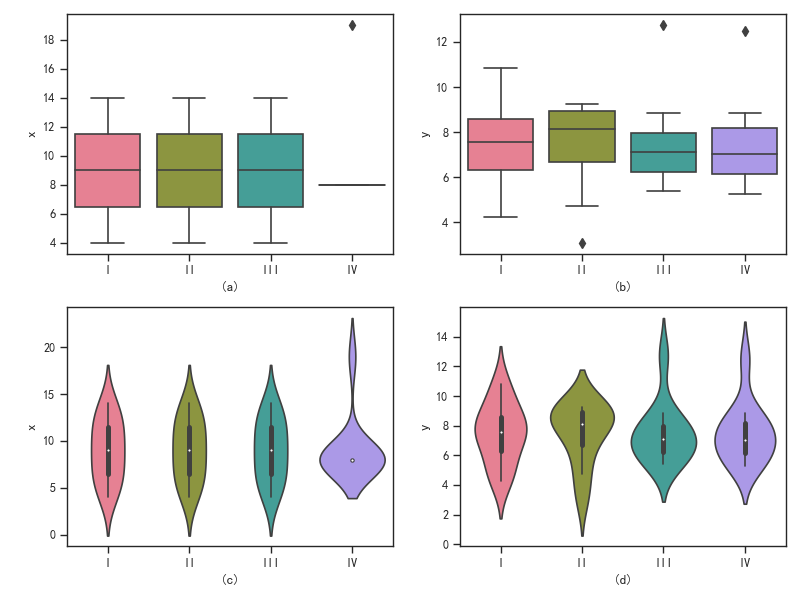
我们可以根据box图或者violin图来看每一组数据分布的区间，可以方便我们判断离群点：
data = pd.read_csv('anscombe.csv')
print(data.head())
sns.set_context('paper')
sns.set_style('ticks',{'font.sans-serif':['simhei','Arial']})
f = plt.figure(figsize=(8,6))
f.add_subplot(221)
sns.boxplot('dataset','x',data = data, palette = 'husl')
plt.xlabel('(a)')
f.add_subplot(222)
sns.boxplot('dataset','y',data = data, palette='husl')
plt.xlabel('(b)')
f.add_subplot(223)
sns.violinplot('dataset','x',data = data, palette = 'husl')
plt.xlabel('(c)')
f.add_subplot(224)
sns.violinplot('dataset','y',data = data, palette = 'husl')
plt.xlabel('(d)')
plt.tight_layout()
plt.show()
由图(c)可以看出第IV组的大部分的数据的x集中在8一点，而y分布与6周围，可以知道y和x的相关性很小，通过(a) (b)我们也可以看到离群点，
(a)至少有一个离群点，分布在x>18范围内，(b)至少有里两个离群点，分布在y>12范围内。
我们可以根据这个来删掉离群点，使得拟合结果更可信。
三维散点图：
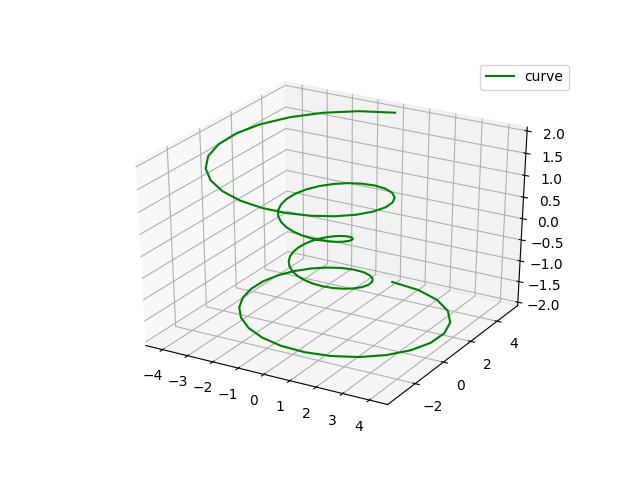
先看三维曲线图：
import matplotlib as mpl from mpl_toolkits.mplot3d import Axes3D import numpy as np import matplotlib.pyplot as plt mpl.rcParams['legend.fontsize'] = 10 fig = plt.figure() ax = fig.gca(projection='3d') theta = np.linspace(-4 * np.pi, 4 * np.pi, 100) #变量theta,决定(x,y,z),所以形成的图形为三维空间中的一维曲线（z与theta是呈线性关系的，绘出100个点。 z = np.linspace(-2, 2, 100) r = z ** 2 + 1 x = r * np.sin(theta) y = r * np.cos(theta) ax.plot(x, y, z, label='curve',color = 'g') ax.legend() plt.show()
再看三维散点图：
from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np from matplotlib import cm plt.rcParams['font.family'] = ['Arial Unicode MS'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 sns.set_style('whitegrid', {'font.sans-serif': ['Arial Unicode MS', 'Arial']}) #用来解决中文方块化的问题 x = np.random.normal(0,2,size = (3,50)) y = np.random.normal(4,2,size = (3,50)) fig = plt.figure(figsize=(10,5)) ax1 = fig.add_subplot(121, projection='3d') ax1.scatter(x[0],x[1],x[2],color = 'r',marker = 'o',label = '红点') ax1.scatter(y[0],y[1],y[2],color = 'b',marker = '^',label = '蓝点') ax1.legend() ax1.set_xlabel('X') ax1.set_ylabel('Y') ax1.set_zlabel('Z') ax2 = fig.add_subplot(122,projection='3d') ax2.scatter(x[0],x[1],x[2],color = 'r',marker = 'o',label = '红点') ax2.scatter(y[0],y[1],y[2],color = 'b',marker = '^',label = '蓝点') x1 = np.linspace(-5,5,100) y1 = np.linspace(-3,8,100) x1,y1 = np.meshgrid(x1,y1) z1 = 6*np.ones(shape = (100,100)) - x1 - y1 ax2.plot_surface(x1,y1,z1,cmap=cm.coolwarm, rstride=1, # rstride（row）指定行的跨度 cstride=1, # 列跨度 linewidth = 0, #线宽最低 antialiased = True) #抗锯齿打开 ax2.legend() ax2.set_xlabel('X') ax2.set_ylabel('Y') ax2.set_zlabel('Z') plt.show()
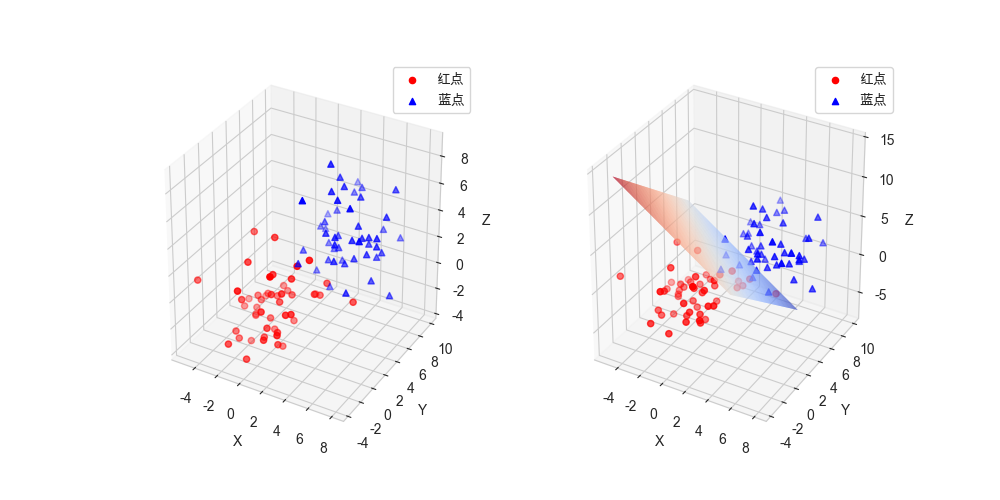
可以看出x + y + z = 6的平面刚好能够把红点和蓝点区分开。
因为红点呈中心为原点的正态分布，蓝点呈中心为（4，4，4）的正态分布，
x+y+z = 6刚好是过两个中心中点的垂直平面，可以将两个正态分布的散点区分开。
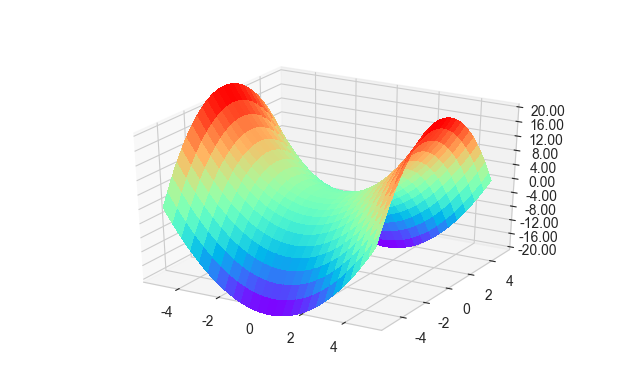
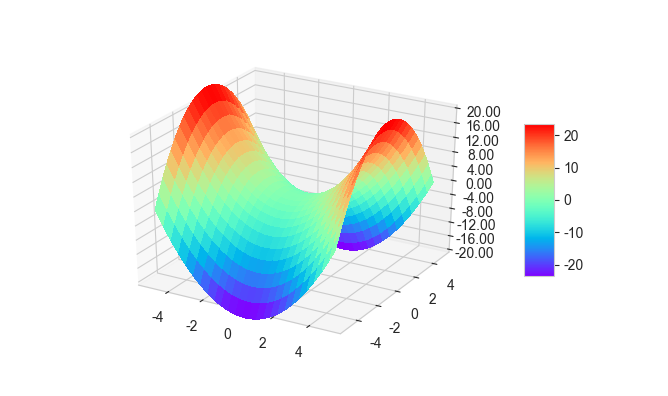
接下来我们要绘制x^2 - y^2 = z的图像 （马鞍面）
三维曲面图：
from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np from matplotlib import cm from matplotlib.ticker import LinearLocator, FormatStrFormatter plt.rcParams['font.family'] = ['Arial Unicode MS'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 sns.set_style('whitegrid', {'font.sans-serif': ['Arial Unicode MS', 'Arial']}) #用来解决中文方块化的问题 x = np.linspace(-5,5,100) y = np.linspace(-5,5,100) x,y = np.meshgrid(x,y) z = x**2-y**2 f = plt.figure(figsize=(5,4)) ax = f.add_subplot(111,projection = '3d') ax.plot_surface(x, y, z, cmap=plt.get_cmap('rainbow'), rstride = 4,cstride = 4, linewidth=0, antialiased=False) ax.set_zlim(-20, 20) ax.zaxis.set_major_locator(LinearLocator(11)) #z方向上均匀分成11-1=10份，即找11个分点， ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f')) #分节点的值保留两位小数 plt.show()
可以看出来当行跨度、列跨度为4的时候，划分曲线显得十分明显，使得整个曲面呈网格状。
另外我们能在plt.show()前面加上 f.colorbar(surf, shrink=.5, aspect=5) #shrink越小，表示colorbar越小
便可以在右边绘制一个colorbar:
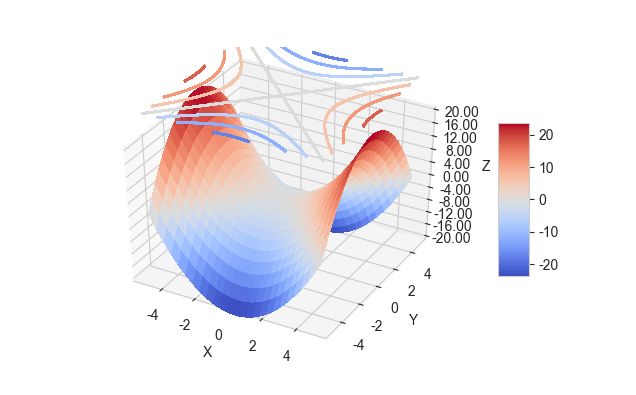
我们从图中也可以看出相近的颜色的点高度都是相同的，我们能否直接绘制等高线呢？
当然可以！
from mpl_toolkits.mplot3d import axes3d import matplotlib.pyplot as plt from matplotlib import cm from matplotlib.ticker import LinearLocator, FormatStrFormatter plt.rcParams['font.family'] = ['Arial Unicode MS'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 sns.set_style('whitegrid', {'font.sans-serif': ['Arial Unicode MS', 'Arial']}) #用来解决中文方块化的问题 x = np.linspace(-5,5,100) y = np.linspace(-5,5,100) x,y = np.meshgrid(x,y) z = x**2-y**2 f = plt.figure(figsize=(5,4)) ax = f.add_subplot(111,projection = '3d') surf = ax.plot_surface(x, y, z, cmap=cm.coolwarm, rstride = 4,cstride = 4, linewidth=0, antialiased=False) cset = ax.contour(x, y, z, zdir = 'z',offset = 30, cmap=cm.coolwarm, antialiased=False) ax.set_zlim(-20, 20) ax.zaxis.set_major_locator(LinearLocator(11)) #z方向上均匀分成11-1=10份，即找11个分点， ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f')) #分节点的值保留两位小数 ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') f.colorbar(surf, shrink=.5,aspect = 5) plt.show()
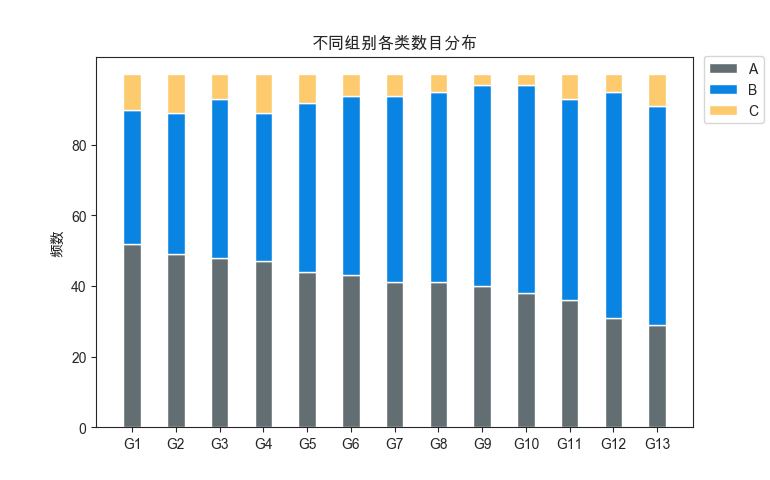
叠加柱状图（用处较大）：
import numpy as np import matplotlib.pyplot as plt plt.rcParams['font.family'] = ['Arial Unicode MS'] # 用来正常显示中文标签 plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号 sns.set_style('ticks', {'font.sans-serif': ['Arial Unicode MS', 'Arial']}) #用来解决中文方块化的问题 N = 13 #含有13组数据 每一组又分为三类A B C,每一类的频数记录其中 A = (52, 49, 48, 47, 44, 43, 41, 41, 40, 38, 36, 31, 29) B = (38, 40, 45, 42, 48, 51, 53, 54, 57, 59, 57, 64, 62) d = [] for i in range(0, len(A)): sum = A[i] + B[i] d.append(sum) C = (10, 11, 7, 11, 8, 6, 6, 5, 3, 3, 7, 5, 9) ind = np.arange(N) #ind表示横轴坐标 width = 0.4 #条形宽度设为0.4 p1 = plt.bar(ind, A, width, color = '#636e72') p2 = plt.bar(ind, B, width, bottom=A, color = '#0984e3') p3 = plt.bar(ind, C, width, bottom=d, color = '#fdcb6e') #最上面一层应该是前面那个相加得到的d作为下限 plt.ylabel('频数') plt.title('不同组别各类数目分布') plt.xticks(ind, ('G1', 'G2', 'G3', 'G4', 'G5', 'G6', 'G7', 'G8', 'G9', 'G10', 'G11', 'G12', 'G13')) plt.yticks(np.arange(0, 81, 20)) plt.legend((p1[0], p2[0], p3[0]), ('A', 'B', 'C'), loc = 'upper right', bbox_to_anchor = (1.13,1.02)) #用两个元组表示legend标签，p[0]表示该图所拥有的颜色 plt.show()
可以看出B类别在每个组都比较多，而A类别在每个组都比较少。
综上就是Python绘图主要用的一些函数及其实例，后面会更新一些有关机器学习算法的总结，大家一起学习，一起进步~
