cf593c

题意：有n(n<=50)个圆，给出每个圆的圆心坐标和半径r(r>=2)。

求两个函数f(t),g(t)，t的取值为0到50的整数，每次令x=f(t),y=g(t)，产生一个51个点的集合。要求这个点集对于每个圆至少有一个点落在圆内或圆周上。

g和f中只能使用常数，加法，乘法，减法，绝对值运算。

输出f和g。

分析：我们设计这样一个多项式，包含n项，当t取值为i的时候，只有第i项的值不为0。其余项均为0。

设计方案是每项都乘以这样一个系数，第i项需要乘以系数1/2×( 1-abs(t-i) + abs( 1 - abs(t-i) ) )。

当只有当i==t的时候该系数才不为0。

原理如下：如果我们设A=1-abs(t-i)的话，那么系数就是（A+abs(A)）/2。

当i=1时，A和abs(A)关于未知数t的图像如下图所示。两者相加只有中间的重叠部分不会抵消。

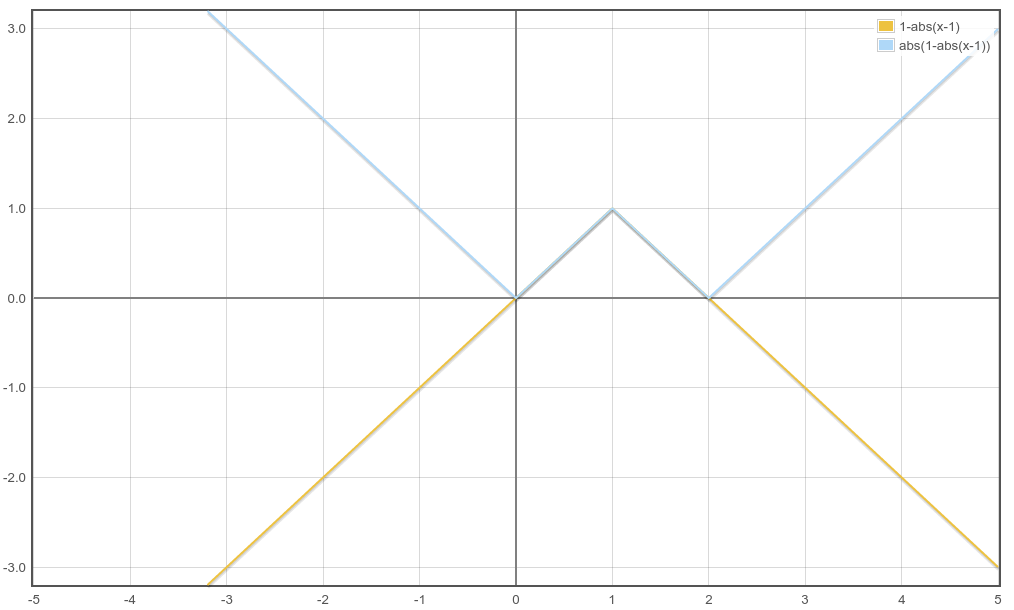
这样我们就让f(t)=sigma(xi/2×( 1-abs(t-i) + abs( 1 - abs(t-i) ) ))，由于圆的半径至少为2，所以xi/2取整带来的误差不会产生影响。

g(t)同理。

#include <cstdio>
#include <string>
#include <iostream>
using namespace std;

int n;

string make(int i, int a)
{
    char st[10];
    sprintf(st, "%d", i);
    string num = string(st);
    string ret = "((1-abs((t-" + num + ")))+abs((1-abs((t-" + num + ")))))";
    sprintf(st, "%d", a/2);
    num = string(st);
    return "(" + num + "*" + ret + ")";
}

int main()
{
    scanf("%d", &n);
    string f = string("0");
    string g = string("0");
    for (int i = 0; i < n; i++)
    {
        int x, y, r;
        scanf("%d%d%d", &x, &y, &r);
        f = "(" + f + "+" + make(i, x) + ")";
        g = "(" + g + "+" + make(i, y) + ")";

    }
    cout << f << endl;
    cout << g << endl;
    return 0;
}