poj1039

题意：几何计算，给出一个管道（一条从左到右的折线，与它向下移动1后的折线构成），问管道最左边发出的光线所能到达的最远位置的横坐标是多少。

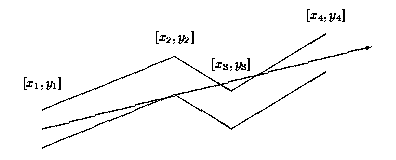
分析：容易知道，要求一个能到达最远的光线，这条光线一定是经过至少两个折线的折点（每个这点可能是上面折线的，也可能是下面折线的），那么我们就每次枚举两个管道折点，求一直线看该直线与管道边缘线段交点。在求的过程中，可以从左到右依次判断是否与各个折点的横断面相交，然后可以得知是否会与管道壁相交。通过直线在横断面对应横坐标的位置的纵坐标高于还是低于横断面。可以判断其与那个管道壁相交，求交点即可。然后在所有交点中找一个横坐标最小的。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
usingnamespace std;

#define maxn 25
#define eps 1.0e-8

struct Point
{
    double x, y;
} point[maxn];

int n;
double ans;
bool ok;

void input()
{
    for (int i =0; i < n; i++)
        scanf("%lf%lf", &point[i].x, &point[i].y);
}

double intersect(Point a1, Point b1, Point a2, Point b2)
{
    double x1 = a1.x, x2 = b1.x, x3 = a2.x, x4 = b2.x;
    double y1 = a1.y, y2 = b1.y, y3 = a2.y, y4 = b2.y;
    double x =(y3-y1+x1*(y2-y1)/(x2-x1)-x3*(y4-y3)/(x4-x3))/((y2-y1)/(x2-x1)-(y4-y3)/(x4-x3));
    return x;
}

void work(Point a, Point b)
{
    b.y -=1;
    for (int i =0; i < n; i++)
    {
        Point p, q1, q2;
        p.x = point[i].x;
        p.y = a.y - (b.y - a.y) / (b.x - a.x) * (a.x - p.x);
        if ((p.y + eps < point[i].y && p.y - eps > point[i].y -1) || abs(p.y
                - point[i].y) < eps || abs(p.y - point[i].y +1) < eps)
            continue;
        if (i ==0)
            return;
        if (p.y - eps > point[i].y)
            ans = max(ans, intersect(a, b, point[i -1], point[i]));
        else
        {
            q1 = point[i -1];
            q1.y -=1;
            q2 = point[i];
            q2.y -=1;
            ans = max(ans, intersect(a, b, q1, q2));
        }
        return;
    }
    ok =true;
}

int main()
{
    //freopen("t.txt", "r", stdin);
while (scanf("%d", &n), n)
    {
        input();
        ans = point[0].x;
        ok =false;
        for (int i =0; i < n; i++)
            for (int j =0; j < n; j++)
                if (i != j &&!ok)
                    work(point[i], point[j]);
        if (ok)
            printf("Through all the pipe.\n");
        else
            printf("%.2f\n", ans);
    }
    return0;
}