算法分析与设计 - 作业 11

目录

• 问题一
  • 解法一
  • 解法二
  • 解法三
  • 解法四
• 问题二
• 解法
• 扩展

问题一

对于一个给定的字符串 \(s\)，给定策略以最少次数将其分割成一些子串，使得某个子串都是回文串。

典中典之最小回文分割。

解法一

发现回文串的分割是无后效性的，即对于字符串前缀 \(s[1:i]\)，若保证了该前缀可以被分为若干完整的回文子串，则它们的分割方案不会影响到之后的分割方案。

则考虑动态规划，记 \(f_{i}\) 表示将字符串前缀分割为若干回文子串的最小分割次数，初始化 \(f_{0} = 0,\ \forall 1\le i\le |s|, f_{i} = +\infin\)，枚举当前被分割的前缀 \(i\)，考虑枚举最后被分出的一段回文串的上一个位置 \(j\) 进行转移，则有：

\[\forall 1\le j< i\le |s|, s[j+1:i]\text{ is a palindrome},\ f_{i} = \min_{j}(f_{j} + 1) \]

答案即为 \(f_{|s|}\)。

上述状态空间复杂度为 \(O(n)\) 级别，考虑在枚举 \(j\) 时暴力检查子串 \(s[j + 1: i]\) 是否为回文串，则转移时间复杂度为 \(O(n^3)\) 级别。

总时间复杂度 \(O(n^3)\) 级别。

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
const int kN = 3e5 + 10;
//=============================================================
std::string s;
int n, f[kN];
//=============================================================
bool check(int l_, int r_) {
  while (l_ <= r_) {
    if (s[l_] != s[r_]) return false;
    ++ l_, -- r_;
  }
  return true;
}
//=============================================================
int main() {
  // freopen("1.txt", "r", stdin);
  std::ios::sync_with_stdio(0), std::cin.tie(0);
  std::cin >> s; n = s.length();
  for (int i = 1; i <= n; ++ i) {
    f[i] = n;
    for (int j = 0; j < i; ++ j) {
      if (check(j, i - 1)) f[i] = std::min(f[i], f[j] + 1);
    }
  }
  std::cout << f[n] - 1;
  return 0;
}

解法二

字符串哈希优化。

字符串哈希是一种用于判重字符串的算法。它将字符串映射到一个整数上，通过判断整数是否相等来判断字符串是否相等。一个字符串为回文串，等价于该字符串与其翻转各位相同。于是可考虑使用字符串哈希，分别构造正串与反串的哈希值来进行子串的判重。

由于字符串是具有前后关系的，一般按下述方法构造：

• 取一个权值 \(𝑐\)，模数 \(𝑝\)。对于长度为 \(n\) 的字符串 \(𝑠\)，有：

\[\operatorname{Hash}(𝑠_1s_2\dots𝑠_𝑛)= 𝑐^{𝑛−1}\times 𝑠_1+𝑐^{𝑛−2}\times 𝑠_2+⋯+c^{0}\times 𝑠_𝑛 \pmod p \]

• 相当于给不同的位置赋上了不同的权值。
• 构造时 \(𝑂(𝑛)\) 递推即得所有前缀的哈希值：

\[\operatorname{Hash}(𝑠_1s_2\dots𝑠_i) = c\times \operatorname{Hash}(𝑠_1s_2\dots𝑠_{i-1}) + s_i \pmod p \]

由上述公式可知对于长度为 \(n\) 的字符串 \(s\)，其子串 \(s_l\sim s_r\) 的哈希值为：

\[\operatorname{Hash}(𝑠_ls_{l+1}\dots𝑠_𝑟)= 𝑐^{𝑟−𝑙}\times 𝑠_𝑙+𝑐^{𝑟−𝑙−1}\times 𝑠_{𝑙+1}+⋯+c^0\times 𝑠_𝑟 \pmod p \]

根据上一步中预处理的前缀哈希值，有：

\[\operatorname{Hash}(𝑠_ls_{l+1}\dots𝑠_𝑟)=\operatorname{Hash}(𝑠_1s_2\dots𝑠_𝑟)−𝑐^{𝑟−𝑙+1}\times \operatorname{Hash}(𝑠_1s_2\dots𝑠_𝑟s_{𝑙−1}) \pmod p \]

预处理 \(𝑐^𝑥\) 后任意子串的哈希值即可 \(O(1)\) 地求得。

考虑 \(O(n)\) 地分别预处理正串与反串的前缀哈希值，而在则在确定了待判定的子串区间后，即可 \(O(1)\) 地求得该子串的正串与反串的哈希值，判断哈希值是否相等即可判断该字符串是否为回文串。动态规划转移总时间复杂度降为 \(O(n^2)\) 级别。

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
const LL p1 = 1e9 + 7;
const LL c1 = 114514;
const int kN = 1e6 + 10;
//=============================================================
std::string s, t;
LL pow1[kN], hs[kN], ht[kN];
int n, f[kN];
//=============================================================
LL hash1(LL *h_, int l_, int r_) {
  return (h_[r_] - pow1[r_ - l_ + 1] * h_[l_ - 1] % p1 + p1) % p1;
}
bool is_palindrome(int l_, int r_) {
  return hash1(hs, l_, r_) == hash1(ht, n - r_ + 1, n - l_ + 1);
}
//=============================================================
int main() {
  // freopen("1.txt", "r", stdin);
  std::ios::sync_with_stdio(0), std::cin.tie(0);
  std::cin >> s; n = s.length();
  t = s; std::reverse(t.begin(), t.end());
 
  pow1[0] = 1;
  for (int i = 1; i <= n; ++ i) {
    pow1[i] = pow1[i - 1] * c1 % p1;
    hs[i] = (c1 * hs[i - 1] + s[i - 1]) % p1;
    ht[i] = (c1 * ht[i - 1] + t[i - 1]) % p1;
  }

  for (int i = 1; i <= n; ++ i) {
    f[i] = n;
    for (int j = 0; j < i; ++ j) {
      if (is_palindrome(j + 1, i)) f[i] = std::min(f[i], f[j] + 1);
    }
  }
  std::cout << f[n] - 1;
  return 0;
}

解法三

Manacher 优化。

Manacher 算法在暴力的基础上，利用了已求得的回文半径加速了比较的过程，可以时空间复杂度均为 \(O(n)\) 级别下求得给定字符串的所有回文子串。

考虑首先在原串的开头、末尾和相邻字符间加入分隔符，使得串长度变为 \(2\times n + 1\)。原串和新串中的回文子串均一一对应，且新串中的回文子串都是有中心奇数长度的串。

考虑在枚举回文子串中心 \(i\) 时维护一个数组 \(p\)，\(p_i\) 表示以 \(s_i\) 为中心的最长回文子串的半径长度。即有：

\[p_i = \max(\{x | x\in \N^+, \forall j < x, s_{i - j} = s_{i + j}\}) \]

同时维护两个变量 \(pos\) 和 \(r\)。\(r\) 代表以某个位置为中心能扩展到的最靠后的位置，\(pos\) 代表上述的位置，则显然有 \(r=pos + p_{pos}-1\)。显然，对于当前枚举到的回文子串中心 \(i\)，由于 \(p_i\ge 1\)，则更新 \(p_{i-1}\) 后至少有 \(r = i-1\)，则有 \(i\in (pos, r+1]\) 成立。

同时，我们记 \(l=pos - p_{pos}+1\) 代表以 \(pos\) 为中心能扩展到的最靠前的位置。显然，由于 \([l,r]\) 是一个回文串，由对称性，则对于以 \(i\) 为中心的某些回文子串，在 \((l, pos)\) 中一定存在一个 \(j\)，满足 \(i + j = 2\times pos\)，且以 \(j\) 为中心的某些回文子串与以 \(i\) 为中心的某些回文子串完全相同。如下图所示：

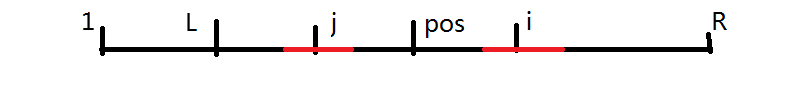
图 1，来源：https://www.luogu.com.cn/blog/Minamoto/solution-p3805

显然，如果我们在计算以 \(i\) 为中心的最长回文子串时，如果可以利用 \(j\) 的信息 \(p_j\)，即可避免大量无用的扩展过程。我们考虑 \(p_j\) 的取值对 \(p_i\) 的影响：

1. 如果以 \(j\) 为中心的最长回文子串的左端点不会越过 \(l\)，即有：\(j - p_j + 1 \ge l\)，则 \(p_{i} = p_j\)，如下图所示。

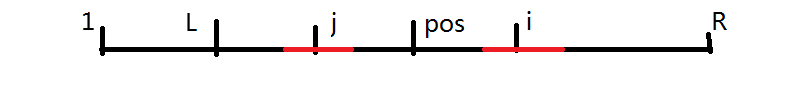
还是上面的图 1，来源：https://www.luogu.com.cn/blog/Minamoto/solution-p3805

2. 如果以 \(j\) 为中心的最长回文子串左端点越过了 \(l\)，即有：\(j - p_j + 1 < l\)，则 \(p_{i} \ge r - i + 1\)，如下图所示。

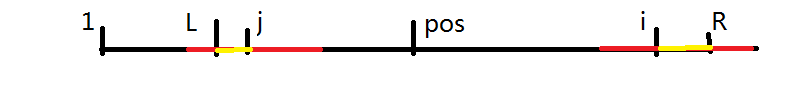
图 2，来源：https://www.luogu.com.cn/blog/Minamoto/solution-p3805

这时我们仅需从第 \(r-i+1\) 位开始以 \(i\) 为中心仅需扩展即可。

再考虑何时应当更新 \(pos\) 的值。我们令 \(pos\) 的初始值为 1，在枚举 \(i\) 过程中，每当计算出一个新的 \(p_i\)，就将 \(r' = i + p_i - 1\) 与当前的 \(r\) 进行比较，如果 \(r'>r\)，则令 \(pos=i, r = r'\) 即可。

注意求得所有 \(p_i\) 后将其转化为原串的回文串长度。显然，对于以新串中位置 \(i\) 为中心的最长回文子串，对应原串中对应位置长度为 \(p_i - 1\) 的最长回文子串。

对于本题，考虑首先调用 Manacher 算法求得所有回文子串，即可 \(O(1)\) 地判断给定子串区间是否为回文串。同样使动态规划转移总时间复杂度降为 \(O(n^2)\) 级别。

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
const int kN = 1e6 + 10;
//=============================================================
std::string s;
char t[kN];
int n, n1, f[kN], p[kN];
//=============================================================
bool is_palindrome(int l_, int r_) {
  // l_ <<= 1, r_ <<= 1;
  return (p[l_ + r_] - 1 >= r_ - l_ + 1);
}
//=============================================================
int main() {
  // freopen("1.txt", "r", stdin);
  std::ios::sync_with_stdio(0), std::cin.tie(0);
  std::cin >> s; n = s.length();

	for (int i = 1; i <= n; ++ i) t[2 * i - 1] = '%', t[2 * i] = s[i - 1];
	t[n1 = 2 * n + 1] = '%';
	int pos = 0, r = 0;
	for (int i = 1; i <= n1; ++ i) {
		p[i] = 1;
		if (i < r) p[i] = std::min(p[2 * pos - i], r - i + 1);
		while (i - p[i] >= 1 && i + p[i] <= n1 && 
					 t[i - p[i]] == t[i + p[i]]) {
			++ p[i];
		}
		if (i + p[i] - 1 > r) pos = i, r = i + p[i] - 1;
	}

  // for (int i = 1; i <= n1; ++ i) std::cout << p[i] << " ";

  for (int i = 1; i <= n; ++ i) {
    f[i] = n;
    for (int j = 0; j < i; ++ j) {
      if (is_palindrome(j + 1, i)) f[i] = std::min(f[i], f[j] + 1);
    }
  }
  std::cout << f[n] - 1;
  return 0;
}
/*
ab
%a%b%
*/

解法四

基于回文串性质，使用回文自动机优化 DP。

时间复杂度 \(O(n\log n)\) 级别。

思路详见：https://oi-wiki.org/string/pam/。

//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
const int kN = 5e5 + 10;
char s[kN];
int n, f[kN], g[kN];
//=============================================================
//=============================================================
inline int read() {
  int f = 1, w = 0; char ch = getchar();
  for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0'); 
  return f * w;
}
namespace PAM {
  const int kNode = kN << 1;
  int nown, nodenum, last, tr[kNode][26], len[kNode], fail[kNode];
  int d[kNode], anc[kNode];
  char t[kN];
  int Newnode(int len_) {
    ++ nodenum;
    memset(tr[nodenum], 0, sizeof (tr[nodenum]));
    len[nodenum] = len_;
    fail[nodenum] = 0;
    return nodenum;
  }
  void Init() {
    nodenum = -1;
    last = 0;
    t[nown = 0] = '$';
    Newnode(0), Newnode(-1);
    fail[0] = 1;
  }
  int getfail(int x_) {
    while (t[nown - len[x_] - 1] != t[nown]) x_ = fail[x_];
    return x_;
  }
  void Insert(char ch_) {
    t[++ nown] = ch_;
    int now = getfail(last);
    if (!tr[now][ch_ - 'A']) {
      int x = Newnode(len[now] + 2);
      fail[x] = tr[getfail(fail[now])][ch_ - 'A'];
      tr[now][ch_ - 'A'] = x;
      d[x] = len[x] - len[fail[x]];
      anc[x] = (d[x] == d[fail[x]] ? anc[fail[x]] : fail[x]);
    }
    last = tr[now][ch_ - 'A'];
  }
  void DP(int i) {
    for (int j = last; j; j = anc[j]) {
      g[j] = i - len[anc[j]] - d[j];
      if (anc[j] != fail[j] && f[g[fail[j]]] < f[g[j]]) g[j] = g[fail[j]];
      if (f[g[j]] + 1 < f[i]) f[i] = f[g[j]] + 1;
    }
  }
}
//=============================================================
int main() {
  // freopen("1.txt", "r", stdin);
  scanf("%s", s + 1); n = strlen(s + 1);
  for (int i = 1; i <= n; ++ i) f[i] = kN;

  PAM::Init();
  for (int i = 1; i <= n; ++ i) {
    PAM::Insert(s[i]);
    PAM::DP(i);
  }
  printf("%d\n", f[n] - 1);
  return 0;
}

问题二

某公司拟在某市开一些分公司，公司分布在不同街道，街道结构可以用一棵树来进行表达。为了避免分公司间竞争冲突，两个分公司不允许开在相邻的街道。（1）若分公司开在不同街道产生的效益相同；（2）分公司开在不同街道产生的效益不同；请分别设计策略使得所开分公司产生的价值最大。

树上最大匹配/ 树上最大带权匹配。

解法

第一问可看做第二问的特殊情况，因为树上该问题有复杂度较优解法，于是仅需考虑第二问。

首先取节点 1 作为根将无根树转化为有根树，则选择的每条边均为父节点连向子节点。

考虑树形动态规划，记 \(f_{u, 0}\) 表示在节点 \(u\) 的子树中，钦定不选择节点 \(u\) 连向父节点的边可取得的最大价值；同理记 \(f_{u, 0}\) 表示在节点 \(u\) 的子树中，钦定可以选择节点 \(u\) 连向父节点的边可取得的最大价值。初始化 \(\forall 1\le u\le n,\ f_{u, 0/1} = 0\)，考虑 DFS 枚举子节点实现树形动态 DP：

对于 \(f_{u, 1}\)，则子节点 \(v\) 均不可与父节点 \(u\) 匹配，则有转移：

\[f_{u, 1} = \sum\limits_{v\in \operatorname{sons}(u)} f_{v, 0} \]

而对于 \(f_{u, 0}\)，子节点 \(v\) 可以与父节点 \(u\) 匹配但仅能匹配一次，则需要找到一个贡献最大的子节点与之匹配，相当于在 \(f_{u, 1}\) 中修改某个子节点的贡献。同时考虑不匹配价值更高的情况，则有：

\[f_{u, 0} = f_{u, 1} - \min\left(0, \min\limits_{v\in \operatorname{sons}(u)}(f_{v, 0} - f_{i, 1} - w(u, v))\right) \]

显然对于所有节点 \(u\) 一定有 \(f_{u, 0}\ge f_{u, 1}\)，则答案即为 \(f_{1, 0}\)。

总时空复杂度均为 \(O(n)\) 级别。

扩展

考虑二分图/一般图最大匹配/最大带权匹配

• 二分图最大匹配：在无权二分图中，Hopcroft–Karp 算法可在 \(O(\sqrt{V}E)\) 解决。
• 二分图最大权匹配：在带权二分图中，可用 Hungarian 算法解决。 如果在最短路搜寻中用 Bellman–Ford 算法，时间复杂度为 \(O(V^2E)\)， 如果用 Dijkstra 算法或 Fibonacci heap，可用 \(O(V^{2}\log {V}+VE)\) 解决。
• 一般图最大匹配：无权一般图中，Edmonds' blossom 算法可在 \(O(V^2E)\) 解决。
• 一般图最大权匹配：带权一般图中，Edmonds' blossom 算法可在 \(O(V^2E)\) 解决。