算法分析与设计 - 作业10
问题一
- 证明:图G中顶点vi到顶点vj之间长度为k的路径数量等于AK的第(i,j)个元素,其中A是图G的邻接矩阵。
设图 \(G\) 中有 \(n\) 个结点,其邻接矩阵为 \(A_{n\times n}\),\(A_{i, j}\) 代表有向边 \(<v_i, v_j>\) 的数量。
考虑数学归纳法。
当 \(k=1\) 时,顶点 \(v_i\) 到顶点 \(v_j\) 之间长度为 1 的路径数量,即为有向边 \(<v_i, v_j>\) 的数量,也即 \(A_{i, j}\)。
当 \(k>1\) 时,已知 \(A^{k - 1}\) 中元素 \(A_{i, j}\) 代表长度为 \(k - 1\) 的路径 \(v_i \rightarrow v_j\) 的数量。由矩阵乘法规则有:
考虑上式的实际意义,相当于枚举了路径中转点 \(v_l(1\le k\le n)\),考虑使用长度为 \(k - 1\) 的路径 \(v_i \rightarrow v_{l}\) 的路径,与长度为 1 的路径 \(v_i \rightarrow v_k\) 拼接成为所需路径,由乘法原理可知其对长度为 \(k\) 的路径 \(v_i\rightarrow v_j\) 的贡献即为上述两部分路径数量之乘积,对于所有路径中转点之贡献求和即为 \(A_{i, j}\)。
容易证明,在上述统计过程中得到的对于两条长度为 \(k\) 的路径 \(v_i\rightarrow v_j\):
- 当中转点 \(v_l\) 不同时,将使得该路径中终点之前的点不同,从而保证两条路径必然不同;
- 当中转点 \(v_l\) 相同时,若构成路径 \(v_i\rightarrow v_j\) 的两部分路径 \(v_{i}\rightarrow v_{l}\) 与路径 \(v_l\rightarrow v_j\) 中有一方不同,则可使得两条路径经过了不同的有向边,从而保证两条路径必然不同。
则上述过程求得 \(A_{i, j}\) 时可保证不重不漏地统计到了所有的路径,归纳可知原结论成立。
问题二
调研线性规划问题求解算法。
研究线性约束条件下线性目标函数极值问题的方法总称,是运筹学的一个分支,在多方面均有应用。一个问题要能转化为线性规划问题,首先要有若干个线性约束条件,并且所求的目标函数也应该是线性的。那么,最容易也最常用的描述方法就是标准型:
已知一组实数 \([a_1..a_n]\) 和一组变量 \([x_1..x_n]\), 在定义上有函数 \(f(x_1..x_n)=\sum_{i=1}^na_ix_i\)。这个函数是线性的。如果 \(b\) 是一个实数而满足 \(f(x_1..x_n)=b\), 则这个等式被称为线性等式,同样的,满足 \(f(x_1..x_n)\leq b\) 或者 \(f(x_1..x_n)\geq b\) 则称之为线性不等式
在线性规划问题中,线性等式和线性不等式统称为线性约束。一个线性规划问题是一个线性函数的极值问题,而这个线性函数应该服从于一个或者多个线性约束。
图解法
当线性规划问题的变量较少时,我们可以使用图解法来直观地解决问题。
比如要求在下列限制下最小化 \(x+y\):
考虑将这些约束在平面直角坐标系中表示:
\(x\leq4\)(红色区域)
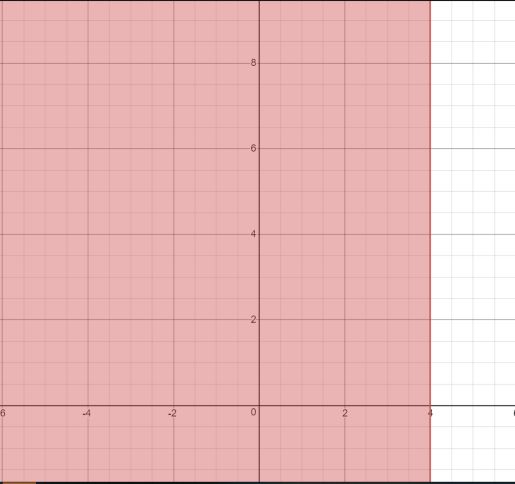
\(y\geq3\)(黑色区域)
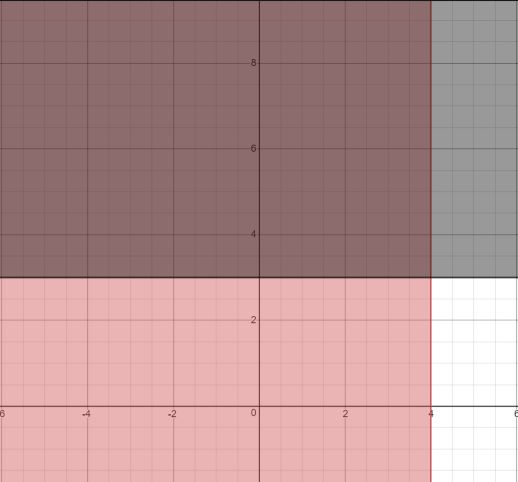
\(3x+y\geq9\)(蓝色直线右侧区域)
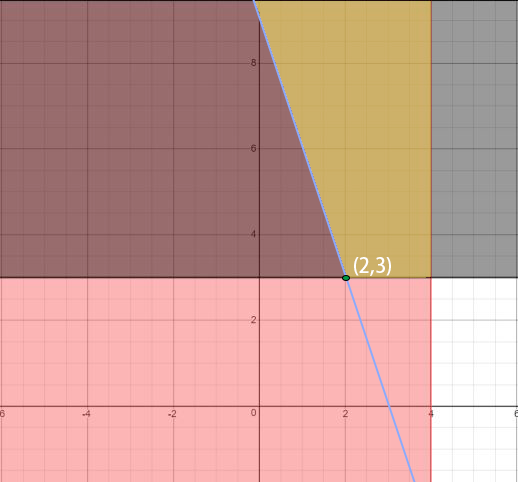
黄色区域为三块区域的交集,这就是这个线性规划的所有可行解。因为题目中说明,需要最小化 \(x + y\),观察图像可知,在点 \((2,3)\),\(x\) 和 \(y\) 同时取到最小值,此时 \(x + y\) 当然最小。因此,\(\min(x + y) = (2 + 3) = 5\)。
把求解线性规划的图解法总结起来,就是先在坐标系中作出所有的约束条件,然后作出需要求极值的线性函数(目标函数)的图像。目标函数中所有点的集合与满足约束条件的所有点的集合的交集就是这个线性规划的解集,而所需求的极值由观察可以轻易得出。
单纯形法
同样考虑将约束在平面直角坐标系中表示,称满足线性规划问题约束条件的所有点组成的集合为线性规划的可行域。若可行域有界(以下主要考虑有界可行域),线性规划问题的目标函数最优解必然在可行域的顶点上达到最优。
单纯形法就是通过设置不同的基向量,经过矩阵的线性变换,求得基可行解(可行域顶点),并判断该解是否最优,否则继续设置另一组基向量,重复执行以上步骤,直到找到最优解。所以,单纯形法的求解过程是一个循环迭代的过程。
标准形
因为单纯形算法是通过线性规划的标准形来求解的,则需要首先定义线性规划的标准形。一般,规定线性规划的标准形式为:
写成矩阵形式:
标准形的形式为:
-
目标函数要求 \(\max\)
-
约束条件均为等式
-
决策变量为非负约束
普通线性规划化为标准形:
-
若目标函数为最小化,可以通过取负,求最大化
-
约束不等式为小于等于不等式,可以在左端加入非负变量,转变为等式,比如:
\[x_1 + 2x_2 \leq 9 \implies \begin{cases} x_1 + 2x_2 + x_3 = 9 \\ x_3 \geq 0 \end{cases} \]同理,约束不等式为大于等于不等式时,可以在左端减去一个非负松弛变量,变为等式。
-
若存在取值无约束的变量,可转变为两个非负变量的差,比如:
\[-\infty \leq x_k \leq +\infty \implies \begin{cases} x_k = x_m - x_n \\ x_m,x_n \geq 0 \end{cases} \]
基变量
在标准形中,有 \(m\) 个约束条件(不包括非负约束),\(n\) 个决策变量,且 \(n \geq m\)。首先选取 \(m\) 个基变量 \(x_j^{'}(j = 1, 2, \ldots, m )\),基变量对应约束系数矩阵的列向量线性无关。通过矩阵的线性变换,基变量可由非基变量表示:
如果令非基变量等于 \(0\),可求得基变量的值:
如果为可行解的话,\(C_i\) 大于 \(0\)。通过选择不同的基变量,可以获得不同的可行域的顶点。
如何判断最优
如前所述,基变量可由非基变量表示:
目标函数 \(z\) 也可以完全由非基变量表示:
当达到最优解时,所有的 \(\sigma_j\) 应小于等于 \(0\),当存在 \(j\),\(\sigma_j > 0\) 时,当前解不是最优解,为什么?
当前的目标函数值为 \(z_0\),其中所有的非基变量值均取 \(0\)。由之前分析可知,\(x_j^{'} = 0\) 代表可行域的某个边界,是 \(x_j^{'}\) 的最小值。如果可行解逐步离开这个边界,\(x_j^{'}\) 会变大,因为 \(\sigma_j > 0\),显然目标函数的取值也会变大,所以当前解不是最优解。我们需要寻找新的基变量。
如何选择新的基变量
如果存在多个 \(\sigma_j > 0\),选择最大的 \(\sigma_j > 0\) 对应的变量作为基变量,这表示目标函数随着 \(x_j^{'}\) 的增加,增长的最快。
如何选择被替换的基变量
假如我们选择非基变量 \(x_s^{'}\) 作为下一轮的基变量,那么被替换基变量 \(x_j^{'}\) 在下一轮中作为非基变量,等于 \(0\)。选择 \(x_j^{'}\) 的原则:替换后应该尽量使 \(x_s^{'}\) 值最大(因为上面已分析过,目标函数会随着 \(x_s^{'}\) 的增大而增大),但要保证替换基变量后的解仍是可行解,因此应该选择最紧的限制。
终止条件
当目标函数用非基变量的线性组合表示时,所有的系数均不大于 \(0\),则表示目标函数达到最优。
如果,有一个非基变量的系数为 \(0\),其他的均小于 \(0\),表示目标函数的最优解有无穷多个。这是因为目标函数的梯度与某一边界正交,在这个边界上,目标函数的取值均相等,且为最优。
使用单纯形法来求解线性规划,输入单纯形法的松弛形式,是一个大矩阵,第一行为目标函数的系数,且最后一个数字为当前轴值下的 \(z\) 值。下面每一行代表一个约束,数字代表系数每行最后一个数字代表 \(b\) 值。
算法和使用单纯性表求解线性规划相同。
代码
#include <bits/stdc++.h>
using namespace std;
vector<vector<double> > Matrix;
double Z;
set<int> P;
size_t cn, bn;
bool Pivot(pair<size_t, size_t> &p) { // 返回0表示所有的非轴元素都小于0
int x = 0, y = 0;
double cmax = -INT_MAX;
vector<double> C = Matrix[0];
vector<double> B;
for (size_t i = 0; i < bn; i++) {
B.push_back(Matrix[i][cn - 1]);
}
for (size_t i = 0; i < C.size(); i++) { // 在非轴元素中找最大的c
if (cmax < C[i] && P.find(i) == P.end()) {
cmax = C[i];
y = i;
}
}
if (cmax < 0) {
return 0;
}
double bmin = INT_MAX;
for (size_t i = 1; i < bn; i++) {
double tmp = B[i] / Matrix[i][y];
if (Matrix[i][y] != 0 && bmin > tmp && tmp > 0) {
bmin = tmp;
x = i;
}
}
p = make_pair(x, y);
for (set<int>::iterator it = P.begin(); it != P.end(); it++) {
if (Matrix[x][*it] != 0) {
// cout<<"erase "<<*it<<endl;
P.erase(*it);
break;
}
}
P.insert(y);
// cout<<"add "<<y<<endl;
return true;
}
void pnt() {
for (size_t i = 0; i < Matrix.size(); i++) {
for (size_t j = 0; j < Matrix[0].size(); j++) {
cout << Matrix[i][j] << "\t";
}
cout << endl;
}
cout << "result z:" << -Matrix[0][cn - 1] << endl;
}
void Gaussian(pair<size_t, size_t> p) { // 行变换
size_t x = p.first;
size_t y = p.second;
double norm = Matrix[x][y];
for (size_t i = 0; i < cn; i++) { // 主行归一化
Matrix[x][i] /= norm;
}
for (size_t i = 0; i < bn; i++) {
if (i != x && Matrix[i][y] != 0) {
double tmpnorm = Matrix[i][y];
for (size_t j = 0; j < cn; j++) {
Matrix[i][j] = Matrix[i][j] - tmpnorm * Matrix[x][j];
}
}
}
}
void solve() {
pair<size_t, size_t> t;
while (1) {
pnt();
if (Pivot(t) == 0) {
return;
}
cout << t.first << " " << t.second << endl;
for (set<int>::iterator it = P.begin(); it != P.end(); it++) {
cout << *it << " ";
}
cout << endl;
Gaussian(t);
}
}
int main(int argc, char *argv[]) {
// ifstream fin;
// fin.open("./test");
cin >> cn >> bn;
for (size_t i = 0; i < bn; i++) {
vector<double> vectmp;
for (size_t j = 0; j < cn; j++) {
double tmp = 0;
cin >> tmp;
vectmp.push_back(tmp);
}
Matrix.push_back(vectmp);
}
for (size_t i = 0; i < bn - 1; i++) {
P.insert(cn - i - 2);
}
solve();
}
/////////////////////////////////////
// glpk input:
///* Variables */
// var x1 >= 0;
// var x2 >= 0;
// var x3 >= 0;
///* Object function */
// maximize z: x1 + 14*x2 + 6*x3;
///* Constrains */
// s.t. con1: x1 + x2 + x3 <= 4;
// s.t. con2: x1 <= 2;
// s.t. con3: x3 <= 3;
// s.t. con4: 3*x2 + x3 <= 6;
// end;
/////////////////////////////////////
// myinput:
/*
8 5
1 14 6 0 0 0 0 0
1 1 1 1 0 0 0 4
1 0 0 0 1 0 0 2
0 0 1 0 0 1 0 3
0 3 1 0 0 0 1 6
*/
/////////////////////////////////////

