Solution Set - “伸手向着拉格朗日点作别”

目录

• 0.「UR #9」「UOJ #133」电路手动分析
• 1.「UR #9」「UOJ #134」App 管理器
• 2.「UR #10」「UOJ #152」汉诺塔
• 3.「UNR #2」「UOJ #312」梦中的题面 ⭐
• 4.「NOI Simu.」战舰
• 5.「UR #10」「UOJ #153」世界线 ⭐
• 6.「洛谷 P9411」Gtrimee
• 7.「CF 1500F」Cupboards Jumps ⭐
• 8.「UR #11」「UOJ #167」元旦老人与汉诺塔
• 9.「NOI Simu.」高维游走 ⭐
• 10.「NOI Simu.」过山车 ⭐
• 11.「NOI Simu.」木棍 ⭐
• 12.「UR #11」「UOJ #169」元旦老人与数列 ⭐
• 13.「UR #12」「UOJ #180」实验室外的攻防战
• 14.「UR #13」「UOJ #186」Yist
• 15.「UR #13」「UOJ #187」Ernd ⭐

$$\mathbb{Defining~\LaTeX~macros\dots} \newcommand{\oreq}[0]{\overset{\lor}{\gets}}$$

  Umm… UOJ 浓度极高的一个 sol set. 摘的标题和上一个 sol set 是姊妹篇!

0.「UR #9」「UOJ #133」电路手动分析

• Link & Submission.

  二分答案, 尽量把选择的结点排成正方形, 计算边数够不够. $\mathcal O(\log\min\{nm,\sqrt r\})$.

1.「UR #9」「UOJ #134」App 管理器

• Link & Submission.

  枚举未定向边 $(u,v)$, 检查去掉这条边后是否存在 $u\to v$ 或 $v\to u$ 的路径, 二者中至少存在一个, 据此定向即可. $\mathcal O(m^2)$.

2.「UR #10」「UOJ #152」汉诺塔

• Link & Submission.
• 「A.构造」

  你这 $10^6$ 的操作限制是来骗人的还是来骗兔的?

  如何利用 $2,3$ 两根空柱子? 把 $1$ 柱子上的盘子依次取出放入 $2,3$ 之一的过程可以看作对 $1$ 柱子序列的一个划分, 结合排序的目标, 那么自然想到上升/下降子序列. 假设 $1$ 从上到下读可以划分为 $k$ 个连续的上升子段, 我们就可以把它们倒到 $2,3$ 上, 在两根柱子上各形成 $k/2$ 个下降子段. 每次取出两个柱子最顶上的子段归并回 $1$, 子段数量 $\div2$. 因此 $\mathcal O(\log n)$ 次迭代后必然完成排序. 操作次数 $\mathcal O(n\log n)$.

3.「UNR #2」「UOJ #312」梦中的题面 ⭐

• Link & Submission.
• 「A.DP-数位 DP」

  数位 DP? 啊, 数位 DP!

  在 $c=1$ 时, $x_i$ 就是 $b$ 进制下的任意 $i$ 位数, 由于 $m$ 个 $b$ 进制数的加法在某一位上的总进位不超过 $m$, 我们可以暴力记录仅考虑低若干位时, $\sum x_i-n$ 在当前位的值. 对 $c=0$, 直接新增一维状态记录有多少个在当前位可以非 $0$ (而非留到最高位变成 $x_i=b^i$) 即可. 最后的状态就是 $f(i,j,k)$ 表示考虑了第 $i$ 位, 有 $j$ 个数可以自由填位, 当前位 $\sum x_i-n=k\in[-1,m]$ 的方案数. 直接转移可以做到 $\mathcal O(m^4b)$. 如果从高位向低位 DP 可以得到四方做法, 不过写着比较麻烦.

4.「NOI Simu.」战舰

• Private link | 卡常, 再见!

• 「B.复杂度平衡」

  横纵坐标上的操作相对独立, 我们可以对每一个横坐标维护其一列上的信息, 纵坐标同理. 移动什么的可以直接合并坐标, 加法和查询按照行列长度根号平衡就行了. $\mathcal O(m\sqrt n)$. 可能有一些很 dirty 的实现细节.

5.「UR #10」「UOJ #153」世界线 ⭐

• Link & Submission.
• 「A.构造」

  对于左侧的下标集合 $S$, 我们尝试找到其在右侧对应的集合 $\{a_i\mid i\in S\}$. 我们可以把左侧连成若干个大小两两不等的连通块, 再在右侧询问出每个连通块, 这样就能根据连通块大小得到对应关系. 为了得到更确定的对应, 自然的 motivation 就是尝试让左侧集合大小两两不同. 我们可以将左侧标号分组:

$$\begin{array}{c|cccc} & 4 & 3 & 2 & 1 \\ \hline 1 & 1 \\ 2 & 2 & 3 \\ 3 & 4 & 5 & 6 \\ 4 & 7 & 8 & 9 & 10 \end{array}$$

可以发现, 左侧的行长度和上侧的列长度构成的坐标可以唯一确定一个单元, 我们就能根据右侧集合所在的行列长度信息直接得到答案.

  这个构造只在 $n=k(k+1)/2$ 时适用, 当 $n\neq k(k+1)/2$, 我们不可能让行列长度都两两不等, 怎么办呢?

  反思一下, 连通块询问带给我们的信息只有 "连通块大小"? 并不是, 我们还可以知道任意两个右侧元素是否在同一连通块, 只不过单用这个信息没办法形成对应关系, 所以在刚刚的构造中没有起作用. 这里有 key motivation: 如果存在且仅存在一个行 (列) 连通块大小为 $1$, 我们可以直接确定某个 $a_p$, 然后根据 $a_p$ 和哪些元素在同一个连通块里确定 $p$ 这一列 (行) 的集合. 这样, 就算两列 (行) 的长度本来相同, 我们也可以根据特殊元素 $a_p$ 来区分它们!

  给出对 $n=k(k+1)/2+r~(r\neq 0)$ 的构造, 这里以 $n=13$ 为例:

$$\begin{array}{c|cccc:c} & 4 & 3^\star & 2^\star & 1 & 1\\ \hline 1 & 1\\ 2 & 2 & 3\\ 3 & 4 & 5 & 6\\ 4 & 7 & 8 & 9 & 10\\ \hdashline 3 & & 11 & 12 & & 13 \end{array}$$

($k^\star=k+1$ 表示自然数 $k$ 的后继, 这样表格好看一点.)

  仍然在两次实验中分别划分行和列询问. 求答案时, 先根据 "行长为 $r$ (只有两行) 且列长为 $1$ (另一行上不可能存在列长为 $1$)" 确定 $a_n$. 然后根据 "和 $a_n$ 属于同一行连通块, 列长依次递减" 得到 $n-r+1\sim n$ 和 $a_{n-r+1\sim n}$ 的所有对应. 接着令 "和某个 $a_i~(i\in[n-r+1,n])$ 同属一个列连通块" 的元素列长 $-1$, 这样就完全消除了最外圈一行一列的影响, 剩下的就和 $r=0$ 一样做了. 加边 $2\times\mathcal O(n)$ 次, 询问 $2\times\mathcal O(n\sqrt n)$ 次.

  怎么办, 越来越喜欢构造题了.

6.「洛谷 P9411」Gtrimee

• Link | 胡.

  Para 怎么问了兔一个经典 trick? 原来 Para 又在卷洛谷的比赛. Para AK 了, 比赛 unrated 了, 可喜可贺.

  GF 入门训练, 先求出任意有根儿子有序无标号树的 GF $F(z)$ (哈哈! 天下谁人不识 Catalan 数?), 则所求树第 $k$ 层结点的子树 GF 是 $F(z)-1$, 再进行 $k$ 次和求 $F(z)$ 一样的迭代就行. 这里的迭代是

$$F^\star(z)=\frac{z}{1-F(z)}.$$

很显然, 令 $F(z)=P(z)/Q(z)$, 这个迭代一次就是对 $\begin{bmatrix}P(z)&Q(z)\end{bmatrix}^T$ 的线性变换:

$$\begin{bmatrix} P^\star(z)\\ Q^\star(z) \end{bmatrix} = \begin{bmatrix} &z\\ -1&1 \end{bmatrix} \begin{bmatrix} P(z)\\ Q(z) \end{bmatrix}.$$

矩阵快速幂即可. $\mathcal O(n\log n\log k)$. 快速幂的结果也可以直接解出来, 这样是 $\mathcal O(n\log n)$ 的.

7.「CF 1500F」Cupboards Jumps ⭐

• Link & Submission.
• 「A.DP-数据结构优化」

  感觉兔的思维习惯变得 contructive & mathematical 了, 根本不会做 OI 题. (雾

  DP! DP! DP! 好看起见, 原题的 $h,w$ 分别换成 $a,b$. 令 $f(i,j)$ 表示构造 $a[:i]$ 使得 $b[:i-2]$ 合法时, $|a_i-a_{i-1}|=j$ 是否可行. 转移:

$$f(i+1,b_{i-1}-j)\oreq f(i,j)\quad (j<b_{i-1}),\\ f(i+1,b_{i-1})\oreq f(i,j)\quad (j<b_{i-1}),\\ f(i+1,k)\oreq f(i,j)\quad (j=b_{i-1},\forall k\le b_{i-1}).$$

注意第三类转移是覆盖性的 "全部合法", 第一类转移是整体位移, 第二类转移只会新增单点. 初始状态 $f(0,\cdot)=\textbf T$ 可以表示为一段足够长的区间, 进而我们可以通过维护大区间和小单点的位移来快速实现转移. 利用状态信息反向构造方案即可. $\mathcal O(n\log n)$.

8.「UR #11」「UOJ #167」元旦老人与汉诺塔

• Link & Submission.

  直觉上有种怪异感, 理论上任意两个合法状态都是可达的, 但步数是指数级别, 合法状态的数量也是指数级别, 我们还要计数而非找最优解. 怎么回事呢?

  那就只能看 $m$ — 如果称 $m$ 是可接受的 "线性" 级别, 那么真正被移动的盘子就只能是 "对数" 级别.

  顺着这个思路发现, 初始状态实际上只有 $3\log_2m$ 个盘子是可能被移动的, 暴力记搜的状态空间是 $\mathcal O(m3^{3\log_2m})=\mathcal O(m^{1+3\log_23})$, 当然这只是毛估, 真正有效状态量自然很少, 能过就对啦.

9.「NOI Simu.」高维游走 ⭐

• Private link & Submission.
• 「A.DP-状压/插头 DP」

  先不考虑疲倦度, 我们先对一个确定的步数序列 $\{a_m\}$ 描述答案, 其中 $a_i$ 即在第 $0$ 阶段 (和第 $i$ 阶段) 的行走步数, 那么这种方案对 $f(\cdot)$ 的贡献为

$$\binom{t_0}{\{a_n\}}\prod_{i=1}^n\binom{t_i}{a_i}\equiv[\forall i\neq j,~a_i\cap a_j=\varnothing][\forall i,~a_i\subseteq(t_i\cap t_0)]\pmod2.$$

这里数的集合运算即对其二进制所表示的集合的运算.

  这一基本的性质告诉我们, 我们只需要考虑满足等式右侧真值式的 $\{a_n\}$. 一个 $\{a_n\}$ 将贡献到 $x=\sum_ii\cdot a_i$ 的 $f(x)$. 由于 $\{a_n\}$ 间两两交集为空这个限制很难在依次枚举 $a_i$ 时记录, 我们更倾向于按位考虑贡献. 设 $p_i$ 表示第 $i$ 个 bit 出现在哪个 $a$ 中, 若未出现则令 $p_i=0$. 那么 $x=\sum_ip_i2^i$. 据此, 我们得到了一个暴力做法: 枚举所有可能的 $\{p_w\}$, 统计出现奇数次的 $x$ 的个数.

  都说啦, 我们倾向于按位考虑贡献. 当只考虑 $\{p_{0..k-1}\}$ 时, $x$ 的低 $k$ 个 bit 已经确定, 此时 $x$ 剩下的 bit 构成的数在 $[0,m]$ 内, 这就产生了对 $x$ 的分类标准. 注意, 我们的最终目标是统计 "同一个 $x$ 出现奇数次" 的数量, 所以这里应该按照 "未确定的长成什么样子" 来划分状态. 设 $f(k,S)$ 表示 {此时有多少个 $x$ 的低 $k$ 位组合满足: 这低 $k$ 位能且仅能与集合 $S\subseteq[:2^m-1]$ 中的整数拼出一个存在奇数次的 $x$}. 我们对于当前 bit 可以出现在的位置集合 $T\in\{0,1\}^m$, 预处理 $(S,T)\mapsto (R_0,R_1)$ 表示状态 $S$ 经过可选集合为 $T$ 的位转移到的新状态, 其中 $R_0$ 表示第 $k$ 位 (转移完成后被确定的位) 是 $0$ 的状态, $R_1$ 同理. 这样转移可以 $\mathcal O(1)$ 完成, 最终复杂度 $\mathcal O(m^22^{2m})-\mathcal O(w2^m)$, 其中 $w=\log V=31$. 预处理也许可以用出色的位运算技巧再优化优化 (啊, 好像不如每次现场算转移哈).

10.「NOI Simu.」过山车 ⭐

• Private link & Submission.
• 「A.图论-网络流-费用流」

  虽然鉴定为不如无限之环, 但不可否认这还是一个有点意思的网络流建图.

  网格图上的简单环一定是二分的, 借此我们可以扔掉诡异的 "存在可行流" 限制, 转而在二染色后描述 "每个点都和两个异色点配对". 我们要求, 若一个点和它的两个配对点贡献, 则不贡献收益, 否则贡献 $a_{i,j}$ 的收益. 换换等价表述, 若一个点在横向两个邻接点和纵向两个邻接点里分别选了一个, 才能贡献 $a_{i,j}$ 的收益. "选得多" 优于 "选得少", 这样就可以描述了:

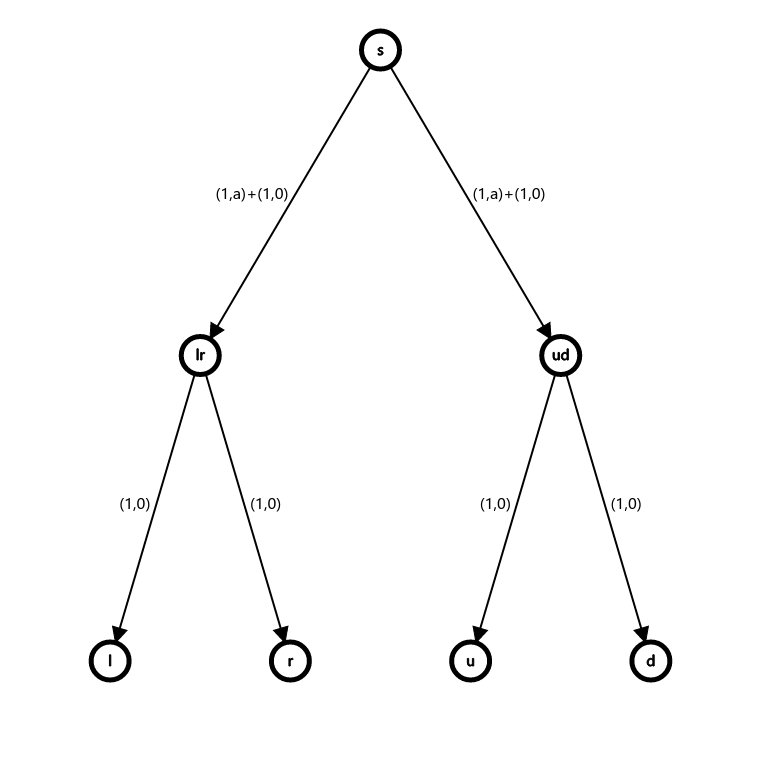
跑最大费用最大流, 若流量合法, 答案就是最大费用减去 $\sum_ia_i$. 复杂度 $\mathcal O(\text{Dinic}(5nm,9nm))$.

11.「NOI Simu.」木棍 ⭐

• Private link | 不想写 (星星眼.jpg
• 「A.图论-差分约束」

  把木棍缩到左端点, 如果 $m=0$ 且 $k=1$, 这就是一个 Hall 定理的事儿. 据此我们也能发现, 把所有端点离散化, 仅考虑区间上 Hall 定理的判据, 仍然是等价的判定.

  一维的规划问题, 想想差分约束? 设 $s_i$ 表示 $i$ 之前放置的木棍数量, 那么限制条件形如 $s_r-s_{l-1}\ge x$. 的确可行. 当 $k\neq1$ 时, 我们就有限制 $s_{i+k}-s_i\le1$, $m\neq0$ 时, 通过 $s_{y_i}-s_{x_i-1}\le c_i$ 也能描述这些要求, 最后加上前缀和的固有条件 $s_i\ge s_{i-1}$, 跑差分约束即可.

  直接 SPFA 最坏 $\mathcal O(n^3)$, 可以通过线段树维护整体转移做到 $\mathcal O(n^2\log n)$.

12.「UR #11」「UOJ #169」元旦老人与数列 ⭐

• Link & Submission.
• 「A.数据结构-线段树」

  Segment Tree Beats!

  嗯, 就用这玩意儿维护就行. 为了更方便维护历史最小值, 我们可以把所有修改标记变成 (当前增量, 前缀增量最小值) 这样的数对, 对区间的最小值和其他值需要分别维护不同的标记. $\mathcal O(n\log^2 n)$.

13.「UR #12」「UOJ #180」实验室外的攻防战

• Link & Submission.

  设 $x$ 在 $a$ 中出现的位置是 $p_x$, 在 $b$ 中出现的位置是 $q_x$, 显然应当满足 $\forall x<y,~p_x<p_y\Rightarrow q_x<q_y$, 有端 (指迅速搓了一发暴力) 猜测这是充要条件, 我们只需要实现快速检查. 若某对 $(x,y)$ 导致非法, 必然有点 $(p_x,q_x)$ 在点 $(p_y,q_y)$ 的左上方. 三维偏序走一走就行, 只需要检查偏序存在性, $\mathcal O(n\log n)$.

14.「UR #13」「UOJ #186」Yist

• Link & Submission.

  若存在可行的消除方案, 则必然存在一种被删除元素递增的删除方案. 假设某个询问串是 $\{s_n\}$, 那么对于某个 $s_i=0$, 它就需要能在序列 $\{a_j\mid s_j=1\lor a_j\ge a_i\}$ 中被第一个删除, 也即存在一个以 $a_i$ 为最小值的长度为 $x$ 的子段.

  可见, 我们只需要求出每个 $a_i$ 对应的最长子段的最小长度就能得到答案. 按值从大到小考虑 $s_i=0$ 的 $a_i$, 将其加入到序列中暴力向左右扩展, 遇到已经被扩展过的结点直接跳过当前检查 (当前子段不短于曾经扩展这个位置的元素), 这样就 $\mathcal O(nq)$ 了.

15.「UR #13」「UOJ #187」Ernd ⭐

• Link & Submission.
• 「A.DP-斜率优化」「B.离线」

  令 $f(i)$ 表示你觉得它该表示的东西, 那么 $f(i)$ 有两类转移:

$$f(i)\overset{\max}{\gets} f(j)+1\quad(|a_i-a_j|\le b_i-b_j),\\ f(i)\overset{\max}{\gets}f(k)+(i-j+1)^2\quad(|a_j-a_k|\le b_j-b_k,[j,i]\text{ is combo-able}).$$

  形如 $|a_i-a_j|\le b_i-b_j$ 的限制可以拆成 $a_i-a_j\le b_i-b_j\land a_j-a_i\le b_i-b_j$, 它也描述了点 $(b_i-a_i,b_i+a_i)$ 和点 $(b_j-a_j,b_j+a_j)$ 的偏序关系, 所以前面一个转移可以根据 $b_i-a_i$ 离线后用 BIT 维护 $y$ 轴上的偏序贡献解决.

  显然, 一列可 combo 的子段在上述离线过程中肯定会被依次取出来, 我们可以在 $j$ 处转移时顺便将 $(j,\max\{f(k)\}+(j-1)^2)$ 放入 $j$ 所在 combo 连续段的凸包上, 在 $i$ 被拿出来的时候就弹一弹凸包进行第二类转移. 最终复杂度 $\mathcal O(n\log n)$.