Solution Set - “带我去看极光与大海吧”

目录

• 0.「AGC 062C」Mex of Subset Sum
• 1.「THUPC 2021 初赛」「洛谷 P7136」方格游戏
• 2.「THUPC 2023 初赛」「洛谷 P9139」喵了个喵 II ⭐
• 3.「THUPC 2021 初赛」「洛谷 P7144」狗蛋和二五仔
• 4.「山东省集 2017」「LOJ #6141」Fantasy
• 5.「CEOI 2021」「洛谷 P8175」Tortoise ⭐
• 6. 「NOI Simu.」dl ⭐
• 7.「PA 2019」「洛谷 P5984」Podatki drogowe ⭐
• 8.「2021 集训队互测」「LOJ #3661」蜘蛛爬树 ⭐
• 9.「NOI Simu.」划分
• 10.「ARC 161A」Make M
• 11.「ARC 161B」Exactly Three Bits
• 12.「ARC 161C」Dyed by Majority (Odd Tree)
• 13.「ARC 161D」Everywhere is Sparser than Whole (Construction)
• 14.「ARC 161E」Not Dyed by Majority (Cubic Graph)
• 15.「洛谷 P7730」蜀道难

$$\mathbb{Defining~\LaTeX~macros\dots} \newcommand{\chkmin}[0]{\overset{\min}{\gets}}$$

0.「AGC 062C」Mex of Subset Sum

• Link & Submission.

  考虑增量地寻找集合. 将 $a$ 排序, 令 $s$ 为其前缀和. 设 $X_i$ 表示 $\{a_{1..i}\}$ 不能表示出的 $\le s_i$ 的数构成的集合. 讨论 $a_i$ 加入时:

  若 $s_{i-1}<a_i$, 则 $X_{i-1}$ 的所有元素都是答案, 若答案足够则终止; 否则, 新增的元素有 $x\in(s_{i-1},a_i)$ 以及 $x-a_i\in X_{i-1}$.

  否则 $s_{i-1}\ge a_i$, 则 $X_{i-1}$ 的所有小于 $s_{i-1}$ 的元素都是答案, 若答案足够则终止; 否则, $X_i$ 在 $X_{i-1}$ 的基础上可以类似地调整.

  通过两个终止条件, 我们可以保持 $|X_i|\le ki$, 这样复杂度就是 $\mathcal O(n^2k)$, 顶多带个 $\log$ 的了.

1.「THUPC 2021 初赛」「洛谷 P7136」方格游戏

• Link & Submission.

  好困… 才把另依托答辩卡常卡完…

  不太有意思的题, 题读对了就没啥问题了. 无障碍矩阵内两两最短路, 矩阵内到矩阵外两两最短路, 绕着矩阵边缘绕的远路都可以分横纵坐标讨论, 手撕两个求和 $\mathcal O(1)$ 算出来. 障碍到障碍间的容斥也可以分坐标讨论, 排序后 $\mathcal O(p)$ 算贡献. 最终 $\mathcal O(p\log p)$ 结束.

2.「THUPC 2023 初赛」「洛谷 P9139」喵了个喵 II ⭐

• Link & Submission.
• 「A.图论-2_SAT」「B.优化建图」

  自然地考察 $2n$ 的情况, 可以发现有解当且仅当同色对构成的 $n$ 个区间两两不存在包含关系. 扩展到 $4n$, 则出现位置依次为 $[p_1,p_2,p_3,p_4]$ 的颜色仅有 $(p_1,p_3),(p_2,p_4)$ 和 $(p_1,p_2),(p_3,p_4)$ 两种子颜色划分方案. 对这个建 2-SAT, 推导关系是二偏偏序, 离线后主席树优化建图即可.

3.「THUPC 2021 初赛」「洛谷 P7144」狗蛋和二五仔

• Link & Submission.

• 「A.模拟」「C.细节」

  搜! 就嗯搜! 所有中间状态全部记忆化!

struct State {
    char ahp, ac1, ac2, ahd; // A's hp, cards with hp=2, hp=3, cards in hand.
    char hv1, hv2; // A's attacked cards.
    char bhp, bc1, bc2, bhd; // B's hp, cards with hp=2, hp=3, cards in hand.
    char prc, rst; // Proceeding /Dapai/, steps available.
};

(抽象派英语喵.) 就搜它就好.

  WA 点:

• 请朗诵三遍输入格式, 我没有开玩笑.
• 注意 "攻击" 不计入操作轮数限制.
• 注意能否实现 "仅攻击一次, 就交换先后手" 这个行为.
• 不建议尝试细节上的贪心, 可能成为小丑.

  TLE 点:

• (本题中) 常数: __gnu_pbds::gp_has_table 小于 std::unordered_map 小于 std::map.
• 就别用十万维数组了, 用上面的东西吧.
• 尽量在哈希表里装 int, 状态在进制 hash 后可能刚好超 int, 拆出来几维开哈希表数组即可. 这个时空优化效果都很明显.
• 如果先手全部攻击后手玩家可以击杀对方, 则直接判定, 这个剪枝没问题.

4.「山东省集 2017」「LOJ #6141」Fantasy

• Link & Submission.
• 「A.图论-最短路相关」

  不完全是正解, 不过也挺有意思. 令 $f(s,t)$ 表示把字符串 $s$ 转换到 $t$ 的最小步数. 当 $s\neq t$ 时, 考察最小的满足 $s_x\neq t_x$ 的 $x$, 我们必然会在某次替换中让 $s_x=t_x$, 枚举最后一次影响到 $s_x$ 的修改对 $(u,v)$, 设 $s^u$ 表示将 $s$ 的后缀替换为 $u$ 得到的字符串, 可见这里需要满足 $s^v[:x]=t[:x]$, 因此有

$$f(s,t)=\min_{(u,v)}\{f(s,s^u)+f(s^v[x+1:],t[x+1:])+1\}.$$

  有环, 不过如果按照 $|s|$ 分层, 层间是无环的, 层内转移可以写作 $f(s,t)\chkmin f(s,s^u)+f(\cdot,\cdot)+1$. 后边的贡献是常数, 分层跑最短路就好. 复杂度怪怪, $(s,t)\to(s,s^u)$ 这个变换不太容易分析复杂度.

  正解也差不多, 首先在 $s_1=t_1$ 时有 $f(s,t)\chkmin f(s[2:],t[2:])$, 此外, 如果我们需要用一对 $(u,v)$ 来修 $s_1$, 就有 $f(s,t)\chkmin f(s,v)+f(v,t)$, 边界有 $f(u,v)=1$. 这个本身就是最短路形式, 不需要像我的做法建抽象的图了. 跑满是 $\mathcal O(Tn^3|s|)$, 好吓人.

5.「CEOI 2021」「洛谷 P8175」Tortoise ⭐

• Link & Submission.
• 「B.贪心」

  设 $d_i$ 表示从 $i$ 出发到最近的游乐园的最短距离. 我们对 $[l,r]$ 这一段极长的不含游乐园的连续段考虑, 不妨取出 $a_p>0$ 中 $d_p$ 最大的 $p$. 若兔子仅在其中卖糖果, 可以感知到贪心策略:

1. 在 $[l,p)$ 里买糖果, 在 $l-1$ 与购买点间横跳.
2. 从 $p$ 带一颗糖到 $r+1$.
3. 在 $[p,r]$ 里买糖果, 在 $r+1$ 与购买点间横跳.

注意若某侧实际上没有游乐园, $p$ 的选取会让对应侧区间为空, $d_p$ 的值可以帮助我们正确计算答案.

  显然, 兔子不会从右侧连续段回到左侧连续段, 我们只需要依次处理这些连续段. 每次尝试取走商店里的所有糖, 再用 heap 退掉已选的代价最高的糖来让时间合法即可. 复杂度 $\mathcal O(n\log n)$.

6. 「NOI Simu.」dl ⭐

• Private link & Submission.
• 「C.性质/结论」

  悄悄告诉你, 一共只有 $\mathcal O((n+q)\sqrt n)$ 次烧树事件! 考虑所有未燃烧的连续段, 对于长度 $<\sqrt n$ 的, 只会在 $\mathcal O(\sqrt n)$ 的时间内产生同级的烧树事件, 对于长度 $>\sqrt n$ 的, 任意时刻不会存在超过 $\mathcal O(\sqrt n)$, $q$ 次放火分析类似.

  因此, 只需要动态维护未燃烧连续段 (一种偷懒的写法是 std::set, 区间端点类型用 mutable 修饰), 用支持 $\mathcal O(1)$ 禁用 / 恢复, $\mathcal O(\sqrt n)$ 查修区间的分块结构维护序列即可. 复杂度 $\mathcal O((n+q)\sqrt n)$.

7.「PA 2019」「洛谷 P5984」Podatki drogowe ⭐

• Link & Submission.
• 「A.分治-二分答案」「A.树论-点分治/点分树」「A.数据结构-可持久化线段树」「B.Hash」「C.Tricks」

  把上面的 tags 连词成句: 用主席树维护权值, 通过 hash 实现 $\mathcal O(\log n)$ 比较两个路径权值和的大小, 这是广为人知的 trick, 此后只需要二分答案, 就差不多做完啦?

  先来看看如何求一个二分的权值和在所有路径中的排名. 我们可以先点分预处理出每个分治中心向外走的权值, 然后枚举分治中心, 双指针求满足 $a+b\le x$ 的两个路径权值和 $a,b$ 的位置, 这样就能求排名了.

  但是, 还有一个问题是, 我们该怎么二分呢? 自然不可能在 $n^n$ 的值域空间上二分, 似乎也没有办法求出哪条路径是 "中点". 这里是一个比较新的 trick: 设答案区间是 $(L,R)$, 我们只需要实现 "在答案区间中均匀随机取出一个 (真实存在的) 路径和" 这个功能, 就能完成分治过程, 复杂度正确. 对于本题, 同上面双指针类似, 用三个指针扫描每个分治中心的序列即可. 这里没有必要排除来自同一个分治子树的路径相加, 它们不会影响路径的数量级.

  最终复杂度 $\mathcal O(n\log^3n)$, 不能实现得太坏.

8.「2021 集训队互测」「LOJ #3661」蜘蛛爬树 ⭐

• Link & Submission.
• 「A.树论-树链剖分」「A.数据结构-线段树」

  显然存在一种从 $s$ 走到 $x$, 走若干次 $a_x$, 然后从 $x$ 走到 $t$ 的路径. 对于 $s\to t$, LCA 为 $p$ 的路径, 讨论 $x$ 的位置:

  第一种情况, $x$ 在 $p$ 子树内, 如图.

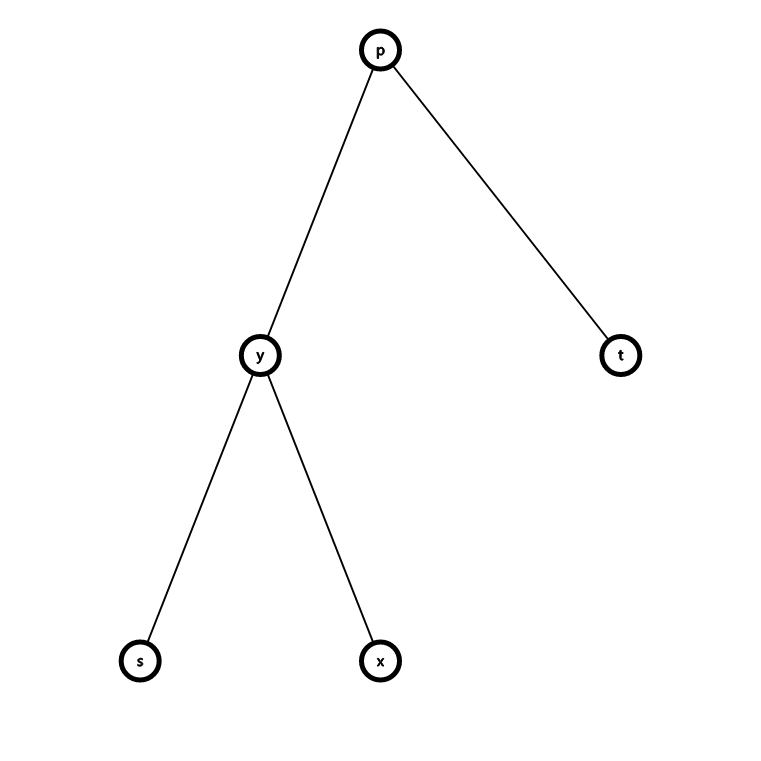
此时路径长度为 $(d_s+d_t-2d_p)+2(d_x-d_y)+ka_x$.

  第二种情况, $x$ 在 $p$ 子树外, 如图.

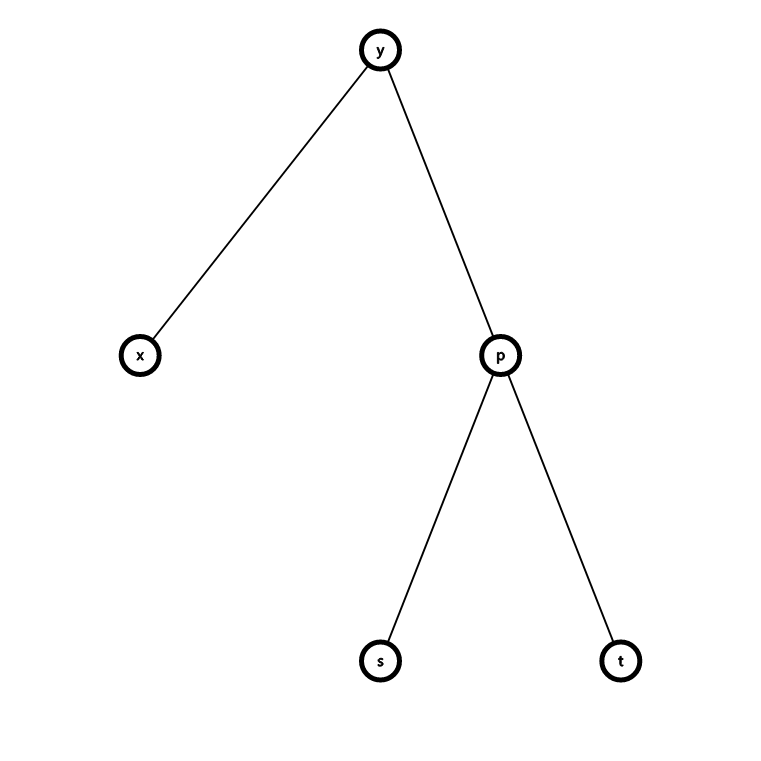
此时路径长度为 $(d_s+d_t)-4d_y+2d_x+ka_x$.

  这些询问操作和 $s,t$ 实际上没什么关系, 我们只关心 $x,y$ 和 $k$ 的取值. 以第一种情况为例, 我们将 $s$ 到 $p$ 的询问挂在若干个重链区间上, 然后对每条重链, 暴力求出以其中的结点为 $y$, 该结点自身或轻子树为 $x$ 时的所有一次函数贡献, 线段树维护区间凸包, 单调地进行询问即可. 对于不加限制的 "$x$ 在 $u$ 子树内" 的询问, 则可以通过一开始维护全局 DFN 上的区间凸包整体求解. 复杂度 $\mathcal O((n+q)\log^2n)$.

9.「NOI Simu.」划分

• Link & Submission.

  你说得对, 但是用十级算法送分是坏文明.

  设 $i\in S$ 的方案数关于此前选择过 $j\in T$ 的数量的 GF 为 $A(z)$, $B(z)$ 同理. 则新加入的一对 $(a_i,b_i)$ 是对 $\begin{bmatrix}A(z)&B(z)\end{bmatrix}^T$ 的线性变换, 直接分治 FFT 即可, $\mathcal O(n\log^2n)$.

10.「ARC 161A」Make M

• Link & Submission.

  排序, 按照 $1,3,\dots,n,2,4,\dots,n-1$ 放到答案里.

11.「ARC 161B」Exactly Three Bits

• Link & Submission.

  不断令 $n\gets n-1$ 直到 $n$ 含有至少三个 bit, 取前三个即可. 迭代次数是 $\mathcal O(1)$ 的.

12.「ARC 161C」Dyed by Majority (Odd Tree)

• Link & Submission.

  尝试取一个根, 依子树归纳构造答案. 对于结点 $u$, 若 $u$ 的已染色儿子已经让 $u$ 的众数无力回天, 则无解, 否则若把所有未染色儿子染成 $u$ 需要的儿子仍然平分秋色 (这也适用于有根叶子的情况), 则对 $u$ 的父亲染色. 这样的构造在保证子树内的解被找到的情况下, 对子树外的颜色提出了尽可能少的要求, 可以感知其正确性. $\mathcal O(n)$.

13.「ARC 161D」Everywhere is Sparser than Whole (Construction)

• Link & Submission.

  若 $n-1<2d$ 则显然无解, 否则令结点编号为 $0\sim n-1$, 排列成一个环. 令 $u$ 连向 $(u+k)\bmod n~(k\in[0,d))$. 此时, 每个点的度数都为 $2d$. 对于大小为 $s$ 的点集, 其内部结点度数和不超过 $2ds$, 而当 $s<n$, 必然存在一条连向集合外的边, 因此诱导子图中所有结点度数和严格小于 $2ds$, 则其密度严格小于 $d$. 完成构造.

---

  是的, 兔告诉你了答案, 简单的二重循环, 轻松的证明. 赛时观榜, 这题通过量一直高于 C. 但是为什么这题卡了兔这么久呢?

  还是有必要回忆一下自己的思路链.

• 这题过那么多? 编个简单点的算法?
• 每次选出度数最小的两个未被连边的点连边?
• 不太良定, 而且不太好写, 弃.
• 导致非法的图是完全图? 最大的合法团是 $K_{2d}$, 比这这个构造?
• 尽量多连边, 先划分出若干个 $K_{2d}$, 团之间的话, 有一些麻烦的度数限制, 例如说不能有一个团外的点连接了团内超过 $d$ 个点.
• 写了一车错解, 换个该死的思路?
• 等等, 我们可以用度数描述边数, 这玩意儿看上去自由度小一点?
• 总度数得是 $2dn$. 我草, 让每个点的度数都是 $2d$ 好像就一定合法了.

  兔得出的结论是: 在那 (指写代码) 之前, 要多想.

14.「ARC 161E」Not Dyed by Majority (Cubic Graph)

• Link & Submission.
• 「A.随机化」「A.图论-2_SAT」

  连词成句: 随机生成答案, 2-SAT 检查合法性, 结束了.

  官方题解看上去是证明远难于其余部分? 溜了溜了, 抱歉 w.

15.「洛谷 P7730」蜀道难

• Link & Submission.

  事情是这样的: 今天有道作业题叫 "蜀道难", 兔点开搜出来的第一道切掉之后才发现其实布置的是那道互测题.

  就, 考虑差分, 每次操作的影响都是一个数 $-1$ 一个数 $+1$, 对建费用流补足所有负的差分位置即可. 复杂度 $\mathcal O(\text{Dinic}(n,nm))$.