Live2D

Diary & Solution Set - 多校度假

目录

\[\mathfrak{Defining~\LaTeX~macros\cdots}\\ \newcommand{\lcm}[0]{\operatorname{lcm}} \newcommand{\vct}[1]{\boldsymbol{#1}} \newcommand{\dist}[0]{\operatorname{dist}} \newcommand{\son}[0]{\operatorname{son}} \newcommand{\addeq}[0]{\overset{+}{\longleftarrow}} \newcommand{\count}[0]{\operatorname{count}} \]

\(\mathscr{Summary}\sim6.14\)

\(\mathscr{Contest}\) \((3/3)\)

  Contest.

  总结等会儿写，好像要走了。

  酒店超级大大大大软枕头导致没睡好，继而使 Min_25 调试 \(1\text{h}+\)，比赛体验感急剧下降。（雾

  颓废好久了，今天算是第一天复健，身边坐着不认识的人貌似让我变自律了（？）

  先开的 T2，这个 \(\mu(p)=f_k(p)\) 的性质太 Powerful Number 了于是开冲，冲到准备写 Powerful Number 发现好像跑不过，而且 Powerful Number 好久没写估计得调很久，所以先放了，看 T1。发现数据范围是 \(w=\) 很大很大和 \(w=\) 很小很小，是针对数据编程？\(w\) 很大比较随便，\(w\) 很小好像不好做啊……

  上了几次厕所，想到了 \(w\) 小的一个合理解释：对于同一个数，它能贡献的询问区间只有近 \(\mathcal O(n)\) 种。各种艰难地解释后得到了正解做法。封在 SmallM 的 namespace 里写出来一看——好像复杂度和 \(w\) 没啥关系昂。😅

  中途浅想了想 T3，发现一个思维难点是：我的贪心（或者其他）解法是能够构造字典序最小方案的，那么常规树上贪心就很很困难……网络流？这个 \(n\le10^6\)……虽说从“题能做”的角度思考问题有时候确实方便，当还是不能忘了思考基础结论啊！然后这题就寄了，最后得到了送温暖的 \(10\text{pt}\)。

  接着写 T2，想着反正复杂度不尽合理不如冲一发 Min_25。Min_25 是啥来着……草稿纸上重新发明了算法（？）调了大半天（宏展开导致运算顺序反逻辑，Min_25 第一阶段还去枚举 \(p_i\) 的指数……）大概 \(12:05\)，样例过了。科学地卡一下常，本地 \(2.1\text{s}\) 极限数据，觉得比较稳，交了。

  最后检查了一下 T1 主席树的空间，最后还是 RE 了，痛失 rk1（虽然给一次修改机会估计大家都是 rk1，没啥好说）。😢

\(\mathscr{A}.\) 区间第 \(k\) 小

  给定 \(n,m\) 和序列 \(\{a_n\}\)。\(q\) 次询问，每次给出 \(l,r,k\)，求将 \(a[l:r]\) 中所有出现次数多于 \(m\) 次的数替换为 \(n\) 后，\(a[l:r]\) 中第 \(k\) 大的值。强制在线。

  \(0\le a_i<n,q\le10^5\)。

  Tags:「A.扫描线」「A.数据结构-树套树」

  原题指明了形如 \(m=5\times10^3\) 和 \(m=10\) 之类的限制，通过迷惑选手增加题目难度属于是。

  先忽略在线，考虑扫描线，从左到右扫描元素，设当前扫描到 \(p\)，\(a_p=x\)，其最近若干次出现位置为 \(i_0,i_1,i_2,\cdots,i_m,i_{m+1}=p\)，那么当左端点 \(l\in(i_1,i_{m+1}]\) 时，\(x\) 的出现次数会在原来的基础上 \(+1\)；当 \(l\in(i_0,i_1]\) 时，本来 \(x\) 在 \([l,r]\) 的出现次数为 \(m\)，但是 \(p\) 让其出现次数超过 \(m\)，所以将 \(l\in(i_0,i_1]\) 时 \(x\) 的出现次数置为 \(0\)（即 \(-m\)）。可以用权值线段树维护这一过程。

  强制在线？主席树套主席树即可，毕竟 \(1\text{G}\) 随便用。复杂度 \(\mathcal O(n\log^2n)\)。

\(\mathscr{B}.\) 求和

  定义积性函数 \(f_k(p^c)=(-1)^c[c\le k]\)，求

\[\sum_{i=1}^n\sum_{j=1}^n\sum_{k=1}^mf_k(\gcd(i,j))\bmod 2^{30}. \]

  \(n\le10^{10}\)，\(m\le40\)。

  Tags: 「A.数学-数论」「A.数学-Min_25 筛」「A.数学-Powerful Number 筛法」

  基础化简：

\[\begin{aligned} \textit{ans} &= \sum_{k=1}^m\sum_{d=1}^nf_k(d)\sum_{i=1}^{n/d}\sum_{j=1}^{n/d}[i\perp j]\\ &= \sum_{k=1}^m\sum_{d=1}^nf_k(d)\left(2\sum_{i=1}^{n/d}\varphi(i)-1\right). \end{aligned} \]

后面反手杜教筛，现在式子长成

\[\textit{ans}=\sum_{k=1}^m\sum_{d=1}^nf_k(d)g(n/d). \]

你大可以直接莽 Min_25，\(\mathcal O\left(\frac{mn^{3/4}}{\log n}\right)\) 能过。

  （嘴巴：）发现 \(f_k(p)=\mu(d)\)，这个时候就很激动地想到 Powerful Number。考虑一下 Powerful Number 搜索过程中对函数值的维护，可以用一个 bit 表示某个 \(f\) 的点值，popcount 一下也能快速求出 \(\sum_k f_k(x)\)。然后类似于杜教筛的优化方法，线性筛（貌似需要再容斥一下）求出 \(f\) 前 \(n^{2/3}\) 个点值，后续的前缀和再用 Powerful Number 算。可以得到 \(\mathcal O(n^{2/3})\) 的算法。（更具体地，可以说是 \(\mathcal O(n^{2/3}\frac{m}{\omega})\)，但 \(m\) 小得可怜 w。）

\(\mathscr{C}.\) 树 *

  给定一棵含有 \(n\) 个结点的树，点 \(u\) 有点权 \(a_u\)，初始为 \(0\)。每次操作指定路径 \(P(u,v)\)，对于 \(e=\lang x,y\rang\in P(u,v)\)，若 \(x<y\)，令 \(a_x\gets a_x+1,a_y\gets a_y+1\)；否则令 \(a_x\gets a_x-1,a_y\gets a_y-1\)。给出最终的点权，构造操作方案。先最小化操作次数 \(m\)，再最小化 \((u,v)\) 序列的字典序。

  \(n\le10^6\)，保证 \(m\le n\)。

  Tags: 「B.贪心」「C.性质/结论」

  被诈骗了 /jk

  注意操作的可合并性，若点 \(u\) 是某个操作的起点，则其一定不是另一个操作的终点，反之亦然。此外，通过考虑每条边被经过的次数，可以发现用每个点作起点（\(+1\)）/终点（\(-1\)）的次数集合可以唯一描述操作的效果。我们只需要求出这一集合，然后贪心构造字典序最小的操作即可。

  如何求呢？还是将子树作为贪心的子结构。令 \(f(u)\) 表示在放置最少的路径的情况下，从 \(u\) 向上走的路径条数（若为负，则是向下走）；\(g(u)\) 表示 \(u\) 作起点的次数。设 \(u\) 的父亲为 \(w\)，孩子们为 \(v\)，那么

\[f(u)=([u<w]-[w<u])\left(a_u-\sum_v([v<u]-[u<v])f(v)\right),\\ g(u)=f(u)-\sum_vf(v). \]

  \(\mathcal O(n)\) 即完成所有工作。

\(\mathscr{+_1}.\) 「CF 1654F」Minimal String Xoration

  Link & Submission.

  给定字符串 \(S=s_0\cdots s_{2^n-1}\)，求一个 \(x\)，最小化 \(S'=s_{0\oplus x}\cdots s_{(2^n-1)\oplus x}\) 的字典序。

  \(n\le18\)。

  Tag: 「B.倍增」

  令 \(S_t\) 为 \(x=t\) 时的 \(S'\)，对 \(\{S_t\}\) 倍增基排即可。复杂度 \(\mathcal O(n2^n)\)。

\(\mathscr{Summary}\sim6.15\)

  数学算麻了。但刷题状态比在校 zhihu.com 的状态好多啦！

\(\mathscr{Topic}\rightarrow\) 数学 \((4/4)\)

\(\mathscr{A}.\) 「NOI 2014」「洛谷 P2354」随机数生成器

  水题。

\(\mathscr{B}.\) 「CF 923E」Perpetual Subtraction ^

  以前的题解。对角化线性变换，经典题。

\(\mathscr{C}.\) 「Gym 102978A」Ascending Matrix *

  Link & Submission.

  Tags: 「A.数学-组合计数」「B.模型转化」「C.Tricks」

  LGV-lemma 已经 \(114514\) 杀兔子了。（

  先不考虑 \(a_{R,C}=V\) 的限制，想想怎么求总方案数，我发现非常困难。

  巧妙转化：画一张 \((N+1)\times(M+1)\) 的网格图，格点左上角为 \((0,0)\)，格点 \((r,c)\) 左下方的格子内填上 \(a_{r+1,c+1}\)。那么 \(a\) 的数量就是：从 \((n,0)\) 向 \((0,n)\) 作 \(K-1\) 条仅向右或向上走的折线，使得折线互不跨越的方案数。对应到 \(a\)，这些折线就是对 \(a_{i,j}=1..K\) 的区域的划分。

  注意若存在跨越，必然存在相邻两条折线的跨越。我们把所有折线沿 \(\vct v=\begin{bmatrix} \frac{\sqrt 2}{2}&\frac{\sqrt 2}{2}\end{bmatrix}^T\) 平移，就能将跨越转化为相交，继而使用 LGV-lemma 对不交路径计数。

  再加上 \(a_{R,C}=V\) 的限制，为了保持路径的等价地位，我们去描述路径的条数，相当于平移之前，需要恰有 \(V-1\) 条路径在 \((R,C)\) 严格上方。在 LGV-lemma 的基础上，把源汇路径写作 \(c_0+c_1x\) 的形式，求出所得矩阵 \(A\) 的 \([x^{V-1}]\det A\) 即可。实现得好大概 \(\mathcal O(k^2\min\{n,m\}+k^4)\)。

  坑点巨多，草。

\(\mathscr{D}.\) 「Gym 103415J」Cafeteria

  Link & Submission.

  Tags: 「A.DP-动态 DP」「C.性质/结论」

  一脸 DDP 的样子，令列向量 \(\vct{f}_i\) 表示一段前缀的 DP 状态（内容是众所周知的），那么字符 \(c\) 对应的转移矩阵 \(V_c\) 形如

\[V_c=\begin{bmatrix} 1\\ ?&1\\ &?&1\\ &&?&1 \end{bmatrix}, \]

其中 \(V\) 从 \(0\) 开始编号，串 \(B\) 从 \(1\) 开始编号，当 \(V_{i,i-1}=[b_i=c]\)。

  但直接 DDP 自然寄了，我们很可能需要几乎线性的做法。于是想到记录转移矩阵与其逆矩阵的前缀积。研究 \(V_c\) 的你矩阵，其形如

\[V_c^{-1}=\begin{bmatrix} 1\\ -1&1\\ 1&-1&1\\ &&&1 \end{bmatrix}. \]

（\(-1\) 的位置取决于 \(V_c\) 中 \(1\) 的位置。）可见 \(V_c\) 的左乘可以 \(\mathcal O(m^2)\) 模拟；\(V_c^{-1}\) 的右乘虽然不太舒服，但还是可以通过按列类和的形式 \(\mathcal O(m^2)\) 计算。每个前缀矩阵中只有 \(\mathcal O(m)\) 个位置参与了答案的计算，注意精细存储。最终复杂度 \(\mathcal O(nm^2+qm)\)。

\(\mathscr{E}.\) 「Gym 103415K」Magus Night *

  Link & Submission.

  Tags: 「A.数学-数论」「A.数学-数学推导」

  设 \(U=\{1,2,\dots,m\}^n\)，令 \(\mathcal A=\{S\subseteq U\}\)，\(\mathcal B=\{S\subseteq U\mid \gcd(S)>q\}\)，\(\mathcal C=\{S\subseteq U\mid \gcd(S)\le q\land\lcm(S)<p\}\)，则答案可以由三个集合的贡献容斥。

  对于 \(\mathcal A\)，显然

\[\sum_{S\in\mathcal A}\prod S=\left(\sum_{i=1}^m i\right)^n. \]

  对于 \(\mathcal B\)，注意到 \(m\) 的范围不太过分，考虑暴力枚举 \(\gcd\)，那么

\[\sum_{S\in\mathcal B} \prod S = \sum_{i=q+1}^m \sum_{S\in\mathcal B} [\gcd(S)=i] \prod S. \]

优化方法比较初等。令

\[t(d)=\left(\sum_{d\mid i} i\right)^n=d^n\left(\sum_{i=1}^{m/d} i\right)^n, \]

则

\[f(d) = \sum_{S\in\mathcal B} [\gcd(S)=d]\prod S = t(d)-\sum_{d\mid d'\land d'>d}f(d'). \]

可以 \(\mathcal O(m\log m)\) 求解。

  对于 \(\mathcal C\)，同时枚举 \(\gcd\) 和 \(\lcm\)，可以得到式子

\[\sum_{S\in\mathcal C}\prod S=\sum_{i=1}^q\sum_{i\mid j\land j<p}\sum_S [\gcd(S)=i\land\lcm(S)=j]\prod S. \]

前两层和式还是可以 \(\mathcal O(m\log m)\) 枚举，重点考察

\[g(i,j)=\sum_S[\gcd(S)=i\land\lcm(S)=j]\prod S \]

的计算。先做简单简化，

\[g(i,j)=i^ng(1,j/i), \]

所以我只需要求 \(g(1,x)\) 的值。注意到一个有趣的事实：\(q\le m\)，而 \(s_i\le \lcm(S)\)，所以当 \(\lcm(S)\) 合法时，序列 \(S\) 一定合法。结合 \(\lcm\) 的性质，自然想到拆开素因子贡献。而根据上述事实，素因子的贡献互不影响，可以直接将素因子贡献乘起来得到答案。因此

\[g(1,x)=\prod_p\left[\left(\sum_{i=0}^{\alpha_p(x)}p^i\right)^n-\left(\sum_{i=1}^{\alpha_p(x)}p^i\right)^n-\left(\sum_{i=0}^{\alpha_p(x)-1}p^i\right)^n+\left(\sum_{i=1}^{\alpha_p(x)-1}p^i\right)^n\right]. \]

可以 \(\mathcal O(m\log\log m\log n)\) 求解（官方题解的复杂度应该有误）。注意到 \(\sum p^i\) 是 \(\mathcal O(m)\) 级别的，通过线性筛预处理自然数幂可以做到 \(\mathcal O(m\log\log m)\)，则总复杂度为 \(\mathcal O(m\log m)\)。

\(\mathscr{Topic}\rightarrow\) 多项式 \((5/7)\)

\(\mathscr{A.}\) 「CF 286E」Ladies' Shop ^

  众所周知，^ 表示做过的题（“跳”，很形象.jpg）。

\(\mathscr{B}.\) 「CF 960G」Bandit Blues

  水题。和建筑师一样的。建筑师的题解。

  然后我为了图省事儿一个「斯特林数-列」+ 暴力枚举最大值位置莽上去，因为模数忘记改调了半天。😰

\(\mathscr{C}.\) 「CF 986D」Perfect Encoding

  水，但高精只能用 Pascal 卡过（在省事的前提下）。

\(\mathscr{D}.\) 「CF 623E」Transforming Sequence ^

  远古题解。DP 选择本身比较无序，所以可以倍增。但是 MTT。

\(\mathscr{E}.\) 「AGC 021F」Trinity *

  Link & Submission.

  Tag: 「A.DP-计数 DP」「A.数学-多项式」

  首先，我不是写的 Tiw 的做法。

  行上状态比较简单，以此划分子问题。令 \(f(i,j)\) 表示考虑了前 \(i\) 列，使用了 \(j\) 行（相对顺序确定而标号未定）的方案数。讨论第 \(i+1\) 行的列 \(\min/\max\) 的情况：

  • 没有新加，列上空或全部来自于已有的 \(j\) 行：\(f(i+1,j)\addeq\left(\binom{j+1}{2}+1\right)f(i,j)\)；
  • 两个都来自 \(j\)，新加 \(k\) 行：\(f(i+1,j+k)\addeq\binom{j+k}{k+2}f(i,j)\)；
  • 有一个来自于 \(j\) 另一个来自于新选的 \(k\) 行中的一行：\(f(i+1,j+k)\addeq2\binom{j+k}{k+1}f(i,j)\)；
  • 两个都来自新选的 \(k\) 行中的一行：\(f(i+1,j+k)\addeq\binom{j+k}{k}f(i,j)\)。

  总而言之：

\[f(i,j)=\left(\binom{j+1}{2}+1\right)f(i-1,j)+\sum_{k=1}^j\binom{j+2}{k+2}f(i-1,j-k). \]

卷积优化一下。复杂度 \(\mathcal O(mn\log n)\)。

\(\mathscr{Summary}\sim6.16\)

  今天 arc 是不是有活动啊。

\(\mathscr{Contest}\) \((3/3)\)

  Contest.

  对于题目质量只能不予置评，被错大样例整死了。

  怎么大家都没有质疑精神呢？

\(\mathscr{A}.\) 小学生物理题

  有 \(n+1\) 条导线串联了节点 \(0,1,\dots,n+1\)，其中 \(0\) 在负无穷远处，\(n+1\) 在正无穷远处，其余点用坐标描述。现在有恰一条导线断路，站在一个节点上，检查该节点是否与 \(0\) 联通的代价为 \(d_i\)，在节点间行走的代价为走过的距离，修复第 \(i\) 条导线的代价为 \(f_i\)。求从 \(1\) 出发，最坏情况下修复好导线的最小代价。

  \(n\le3\times10^3\)。

  Tag: 「A.DP-单调队列优化」

  发现肯定不会检查 \(0\) 和 \(n+1\)，所以可以把 \(0\) 挪到 \(1\) 的位置，\(n+1\) 挪到 \(n\) 的位置，初始时从 \(0\) 出发，这样就没有“无穷远”的特殊性了。先想暴力，令 \(f(l,r,0/1)\) 表示已知断路位置在节点 \(l,r\) 之间，现在站在 \(l/r\) 时，……的最小代价。那么

\[f(l,r,0)=-s_l+\min_{p\in(l,r)}\{s_p+d_p+\max\{f(l,p,1),f(p,r,0)\}\},\\ f(l,r,1)=s_l+\min_{p\in(l,r)}\{-s_p+d_p+\max\{f(l,r,1),f(p,r,0)\}\}. \]

注意到若 \([l,r]\subseteq [L,R]\)，则 \(f(l,r,t)\le f(L,R,t)\)。于是当固定 \(l\) 或 \(r\) 时 \(\max\) 取的项关于 \(r\) 或 \(l\) 具有单调性。指针维护 \(\max\) 取值分界点，单调队列维护可选值的最小值即可。复杂度 \(\mathcal O(n^2)\)。

  被卡常了，懒得卡 qwq。

\(\mathscr{B}.\) 数轴变换 *

  维护一根数轴。初始时 \(0\) 为黑色，其余整点为白色。进行 \(q\) 次操作：

  1. 单点染黑。
  2. 将所有黑点附近距离不超过 \(x\) 的整点染黑。
  3. 反转区间 \([l,r]\)。
  4. 回退到历史状态。
  5. 单点查询。

  \(q\le2\times10^5\)，坐标不会爆 long long。

  Tag: 「A.数据结构-可持久化平衡数」

  由 \(2\) 操作启发，注意到一个点被染黑多次并不影响答案，尝试维护差分序列。由于 \(+1\) 和 \(-1\) 在 2 中的移动方向不同，所以得用分开维护它们。现在 \(1,2,5\) 理论上好做了，\(4\) 加个持久化问题不大。问题在于 \(3\)，据说是一个 trick：在左右加无实际效果的 \(+1\cdots-1\cdots\) 使得 \([l,r]\) 内的差分标记构成匹配括号串，然后将括号串翻转（不是单纯 reverse，是真的“翻”）。总之 \(\mathcal O(q\log q)\) 能做。

\(\mathscr{C}.\) 中学生物理题 *

  给定平面上 \(n\) 块跨 \(1\times1\) 网格对角线摆放的平面镜坐标，求给镜子四染色的方案，使得任何可能的垂直水平光路形成的环中，经过每种颜色的镜子次数相同且均为偶数。（被镜子两面各反射一次，算经过两次。）

  \(n\le5\times10^5\)。

  Tags:「A.构造」「A.图论-欧拉路」「B.模型转化」「C.性质/结论」

  可见，对一面镜子的真正限制并不是环的内部，而是镜子两面所涉及的两环之间的协调。

  如果只二染色？一种视角是利用欧拉回路“每条边恰好经过一次”的条件。需要认清的是，所谓的“点”“边”其实是具体题目中对象的抽象体现。对于本题，令环为“点”，镜子为“边”，一个环总会一进一出，是否可以将欧拉路黑白染色，使得环上黑白总相等？

  正确的。特别地，为无穷远处间一个虚点，包含在环内的镜子提供一条自环，我们可以直接欧拉回路。

  四染色？先二染色再二染色！在二染色的基础上，去黑白边的生成子图再二染色一次。除虚点外的结点度数为 \(8\) 的倍数是必要条件，而在这一条件成立的前提下，可以验证欧拉路总存在。复杂度 \(\mathcal O(n)\) 解决。

\(\mathscr{Summary}\sim6.17\)

\(\mathscr{Summary}\sim6.18\)

\(\mathscr{Summary}\sim6.19\)

\(\mathscr{Summary}\sim6.20\)

  前几天因为以学考为主的破事儿耽搁了，也许会补上。（咕

\(\mathscr{Contest}~(3/3)\)

  Contest.

  问题是，最后 \(40~\text{min}\) 才发现 A 是签到真的合理吗？

\(\mathscr{A}.\) 益智游戏

  把 \(n\times n\) 的网格图中所有 \(n^2\) 个格子各自划分为 \(2\times 2\) 的小网格，并在其中放上一块骨牌。给出初始骨牌放置方案，改变 \((i,j)\) 上骨牌方向的代价为 \(a_{i,j}\)，求最少的代价，使得不存在一个 \(2\times2\) 的小网格的对角线都被骨牌覆盖。

  \(n\le2\times10^3\)。

  Tags:「A.DP-杂项」「C.性质/结论」

  （上面的题意写得像狗屁，但我懒死了。）

  手玩一下结论，发现左置骨牌的左侧一定是左置骨牌，其余方向结论类似。然后发现：

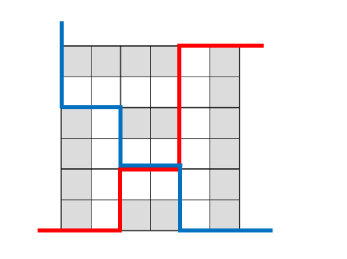
gnp.png

  对分割点的上下左右四部分分别 DP 求最优方案即可。复杂度 \(\mathcal O(n^2)\)。

\(\mathscr{B}.\) 华为 *

  给定 \(n,m,p\) 与 \(T\) 此询问 \((x_i,y_i)\)，初始时 \(x=y=0\)，每次操作以 \(p\) 的概率令 \(x\gets (x+1)\bmod n\)，否则令 \(y\gets (y+1)\bmod m\)，求 \(x=x_i\land y=y_i\) 时的期望操作次数。答案模 \(998244353\)。

  \(n\le10^9\)，\(m,T\le400\)。

  Tags: 「A.多项式」「B.向量/矩阵优化」

  \(\mathcal O((n+m)^3)\) 的就不说了。注意到 \(n\) 的量级与 \(m\) 不同，令 \(f(i,j)\) 表示 \(x=i,y=j\) 出发逆向操作到 \(x=y=0\) 的期望操作次数，尝试强行拆开 \(m\) 方向上（行上）的转移环，观察列上 \(f(i,\star)\) 整体的变化。令 \(q=1-p\) 为操作施加到 \(y\) 的概率。因为

\[f(x,y)=pf(x-1,y)+qf(x,y-1)+1, \]

去消除 \(f(x,y-1)\) 这项，直接枚举 \((x,y)\) 最终从哪个 \(y'\) 走到 \((x-1,y')\)，那么

\[f(x,y)=\frac{1}{1-q}+\sum_{i=0}^{m-1}f(x-1,y-i)\frac{pq^i}{1-q^m}. \]

令 \(F_x(z)=\sum_{i=0}^{m-1}f(x,i)z^i\)，那么

\[F_x(z)=\frac{1-z^m}{(1-q)(1-z)}+F_{x-1}(z)\times \frac{p(1-z^{qm})}{(1-q^m)(1-z^q)}, \]

其中 \(\times\) 是模 \(z^m\) 意义下的循环卷积。注意到这是对 \(F\) 的线性变换，立马想到矩阵加速。令

\[V=\begin{bmatrix} \frac{p(1-z^{qm})}{(1-q^m)(1-z^q)} & \frac{1-z^m}{(1-q)(1-z)}\\ 0 & 1 \end{bmatrix}, \]

则 \(f(x,y)=[z^y](V^x\begin{bmatrix}F_0(z) & 1\end{bmatrix}^T)^{(1)}\)。

  问题是，我们并不知道 \(F_0(z)\)。结合暴力做法，直接拿出 \(F_{n-1}(z)\) 表示 \(F_0(z)\)，解一解方程即可。复杂度 \(\mathcal O(m^3+Tm\log m\log n)\)。

\(\mathscr{C.}\) 区间距离 *

  给定 \(a_{1..n},b_{1..n}\)，\(q\) 次询问，每次给出 \(p_1,p_2,l\)，求出

\[\sum_{i=0}^{l-1}|a_{p_1+i}-b_{p_2+i}|. \]

  \(n\le10^5\)，\(q\le10^6\)，\(1\le a_i,b_i\le V=5\)。

  Tag: 「A.分块」

  暴力循环可以过十万方，并且我发现三目有时比一维 int 数组寻址快。

  分块，就每 \(\omega\) 一块，因为询问涉及到对 \(a\) 的位移，所以块小一点可以以更小的损失对齐整块。预处理每个小位移 \(r\in[0,\omega)\)，整块位移 \(R\in[-n/\omega,n/\omega]\) 的情况下，\(a\) 的前 \(k\) 个块与 \(b\) 的前 \(k\) 个块对应的答案。把 \(|x-y|\) 拆成 \(\sum_c [[x\le c]\neq[y\le c]]\) 数一数 bit 即可。复杂度 \(\mathcal O(Vn^2/\omega+q\omega)\)。

\(\mathscr{Summary}\sim6.21\)

\(\mathscr{Contest}~(3/3)\)

  Contest.

  从头暴力到尾，比较稳健就是了。

  个人感觉 T2 T3 部分分不大合理，像我这种纯暴力选手得分太多了。（

  T1 比较尴尬，写了个根号（而且可能是伪的）算法然后开始卡 \(\log\)，没想到正解是 polylog 的。掉坑里走不出来了。

\(\mathscr{A.}\) 给国的道路 *

  给定无向图 \(G\)，结点 \(u\) 有点权 \(a_u\)。\(E_G\) 初始为 \(\varnothing\)，但是提供了可选的边集 \(E=\{(u,v,s)\}\)。当 \(G\) 中 \(u,v\) 不连通且 \(u,v\) 连通块点权和 \(\ge s\) 时，\((u,v,s)\) 可加入 \(E_G\)。求最长的、再字典序最小的边加入方案。

  \(n\le10^5\)，\(m\le2\times10^5\)，\(a_i,s\le10^6\)。

  Tags: 「A.并查集」「B.Tricks」

  设边 \((u,v,s)\) 当前还需要 \(r\) 的点权和才能加入 \(G\)，在每个连通块上用堆维护二元组 \((r/2,(u,v,s))\)。注意我们对 \(r\) 的更新是惰性的：拿出最小的 \((r/2,(u,v,s))\)，若 \(r/2\le 0\)，重新算一遍得到一个 \(r'\)，根据 \(r'\) 再来决策是否加入边。每条边最多被误判（拿出来又放回去）\(\mathcal O(\log V)\) 次。Splay 实现启发式合并可以做到 \(\mathcal O(n(\log n+\log V))\)。

  （然后发现 pb_ds 的 tree<..., splay_tree_tag, ...> 跑出来还没 std::set 快。）

\(\mathscr{B.}\) 给国与时光机 *

  考虑数轴上的整点 \(0..2n+1\)，其中 \(1..2n\) 被 \(n\) 个传送门两两配对。走 入一个点时，必须 传送 到另一个点。从 \(0\) 出发走到 \(2n+1\)，已知 \(\{(a_i-1,a_i)\}_{i=1}^m\) 是所有被走过的线段，构造配对方案或声明无解。

  \(n\le10^5\)。

  Tag: 「A.构造」

  把 \(0..2n\) 分为 \(A,N,L,R\) 四个集合，分别表示 \(x\) 两边都走过/都没走过/只走过左/只走过右。显然传送门只能在 \(A^2,N^2,L\times R\) 里选。\(N^2\) 随意就好，如果 \(2\nmid|N|\) 则不合法。结合 \(m=2n+1\) 的暴力，可知 \(2\nmid|A|\) 不合法；\(4\mid|A|\) 时 \(A\) 可以四个一组交错配完，\(L,R\) 相邻配；否则 \(|A|=4k+2\)，留两个 LR 配对，把夹着 LR 的一对 AA 配对即可。复杂度 \(\mathcal O(n)\)。

\(\mathscr{C.}\) 给国与赌场 *

  卢老爷拿着 \(\frac{a}{b}<1\) 块钱准备赢到不少于 \(1\) 块钱。每次他可以投注任意正实数金额 \(r\in(0,\frac{a}{b}]\)，但必须不小于上次投注金额，此后以 \(p\) 的概率得到 \(2r\) 块钱，否则血本无归。求最优策略下达到目标的概率。

  \(b\le10^6\)，\(p<\frac{1}{2}\)。

  Tags: 「C.思维」「C.性质/结论」

  一个比较好猜也比较好证的结论：每次投注现有本钱 \(x\) 的二进制小数表示下的最低 bit。这是因为若投注的不是最低 bit，则无论赢钱与否，最低 bit 都没法再使用，也没法对 \(\ge1\) 产生任何贡献。

  那么当 \(a/b\) 是有限小数时就可以直接模拟了，否则，对于完全不会数学的兔来说还是非常困难。

  然后我被神谕了结论：我们还有一种贪心策略：若 \(x<\frac{1}{2}\)，all in；否则投注 \(1-x\)。注意到上一个结论的证明其实可以说明要不要求投注递增这一要求，我们的策略都是优的，所以这里直接忽略。

  设在这种策略下，\(f(x)\) 表示本金 \(x\) 的获胜概率，则

\[f(x)=\begin{cases} p+(1-p)f(2x-1), & x\ge\frac{1}{2}\\ pf(2x), & x<\frac{1}{2} \end{cases}. \]

​  可以证明这种策略与 lowbit 策略等价。如图：

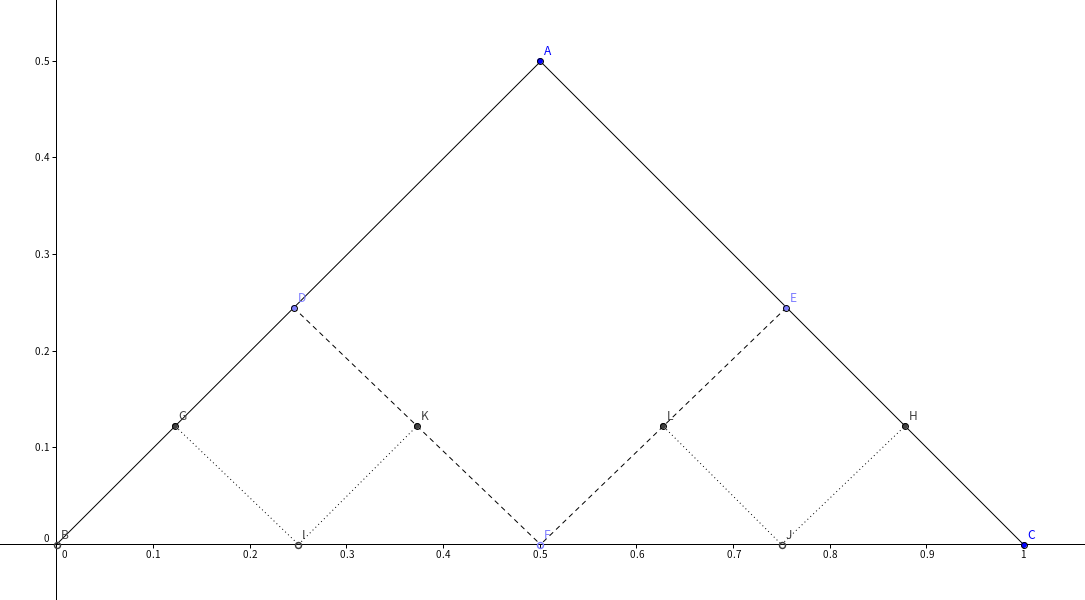
proof.png

单次迭代可以把大三角形拍成两个小三角形（注意点的开闭），足够的迭代后每个位置的取值都是自己的 lowbit。

  拿着 \(f(x)\) 做就比较好办了。设 \(f(a/b)=z\)，迭代 \(f(*/b)=kz+b\)，得到一个 \(\rho\) 形迭代过程，通过环或者 \(a=0\) 的位置把 \(z\) 解出来即可。复杂度 \(\mathcal O(b)\)。

\(\mathscr{Summary}\sim6.22\)

  【洛天依AI】贝加尔湖畔【你清澈又神秘】_哔哩哔哩_bilibili

  都给我去听！！！！！！！！！

\(\mathscr{Class}\rightarrow\) 思维向杂题 \((9/9)\)

  注：本节的星号 * 标记可能有歧义，毕竟怎么都浅听过一遍讨论的。因此将其弃用。

\(\mathscr{A.}\) 「CF 1458C」Latin Square

  Link & Submission.

  Tag: 「B.Tricks」

  Trick: 注意到对 \(p\) 求逆相当于 \((i,p_i)\rightarrow (p_i,i)\)，那么把 \(p_i\) 也当作一维坐标。

  所以需要维护三维坐标集合 \(\{(x,y,z)\}\)，支持一个坐标整体位移、两维坐标整体交换。拿常数个标记就能 \(\mathcal O(1)\) 维护。所以复杂度为 \(\mathcal O(\sum n^2+\sum m)\)。

\(\mathscr{B.}\) 「ICPC EC-Final 2020」「Gym 103069C」Random Shuffle

  Link & Submission.

  Tag: 「A.Gauss 消元」「C.性质/结论」

  这个 xor-shift 发生器生成的数的每个 bit 必然是种子的 \(64\) 个 bit 的一个线性组合。通过反向还原 \(a\) 可以得到第 \(i\) 次生成的数 \(x_i\) 模 \(i\) 所得余数 \(r_i\)，即 \(x_i=r_i+k\cdot i~(k\in\mathbb N)\)。于是，我们可以借此确定 \(x_i\) 低于 \(i\) 的 lowbit 的 bit 与 \(r_i\) 的对应 bit 相等，继而构造关于 \(x\) 的 bit 的线性方程组。最贫困的 \(n=50\) 时，我们会得到 \(47\) 个方程，除去线性相关的东西大概有不超过 \(20\) 个自由元，暴力枚举它们的取值 check 一下即可。

  设方程有 \(c\) 个自由元，\(\omega=64\) 为 bit 数，复杂度最坏为 \(\mathcal O(2^c(\omega+n))\)。需要位运算稍精细实现。

\(\mathscr{C.}\) 「THUPC 2021」「洛谷 P7606」混乱邪恶

  Link & Submission.

  Tags: 「A.DP-数据结构优化 DP」「B.std::bitset」

  背包是一个 \(n\times n\times n\times m\times m\) 的 TF 状态，std::bitset 扬掉最后一维，经典随机化根号 trick 扬掉两个 \(\sqrt n\)，选一选阈值，\(\mathcal O(\frac{n^2m^2}{\omega})\)，当然至少有个枚举方向的 \(6\) 的常数。

\(\mathscr{D.}\) 「JOISC 2022」「UOJ #731」制作团子 3

  Link & Submission.

  Tags: 「A.构造」「C.非传统-交互题」（为了不污染 tag，带「构造」的默认带「思维」。）

  如何判断一个集合 \(S\) 是否存在重复的团子？——询问 \(U\setminus S\)，若回答 \(a=m-1\)，则表明 \(S\) 无重复团子。

  进一步，思考 \(a\) 的意义：其表示 \(S\) 内出现最多的团子数量。

  猜测 \(5\times10^4=5nm=\lceil\log m\rceil nm\)，二分？利用鸽巢原理，可以简单得到一个基于增量法的构造：令 \(m\) 个集合 \(S_{1..m}\) 为 \(m\) 串团子，尝试将当前团子 \(x\) 放入其中一个使其仍合法。每次取可能集合的一半 \(\mathcal T\)，得到 \(\{x\}\cup\{S\in \mathcal T\}\) 中出现最多的团子数量 \(a\)。若 \(a\le |\mathcal T|\)，则 \(\mathcal T\) 中存在一个可加入 \(x\) 的集合；否则 \(\mathcal S\setminus \mathcal T\) 中存在，递归询问就好。操作次数为 \(\mathcal O(nm\log m)\)。

\(\mathscr{E.}\) 「集训队互测 2022」Were You Last @

  @ 是嘴巴，表示口糊，因为 OJ 上莫得。

  交互题。实现函数 bool WereYouLast(int n, int m)，其返回状态能且仅能依赖于 \(n,m\) 以及交互库提供的 \(m\) 个 bit 长的寄存器。且每次调用时，仅能对其中不超过 \(6\) 个 bit 进行读和（或）写。要求其恰好在第 \(n\) 次调用时返回 true。

  \(m=10^5\)，\(n=2^k\le2^{26}\)，\(k\in\mathbb N\)。

  Tags: 「A.构造」「C.非传统-交互题」

  我确实编不出 motivation 了，总之我们用 \(5+26\) 个 bit 构成了一个 pointer 和一个 pool。pointer 指向 pool 的一个位置 \(p\)。则函数行为如下：

  1. 读出 \(p\)。
    • 若 \(p=\log n\)，返回 true。
  2. 读出 \(p\) 指向 bit 的值 \(x\)。
    • 若 \(x=0\)，令 \(p\gets0\)；
    • 否则 \(x=1\)，令 \(p\gets p+1\)。
  3. 令 \(x\gets\lnot x\)。
  4. 返回 false。

不难证明，\(p\) 第一次取到 \(p_0\) 时，是第 \(2^{p_0}\) 次调用。这真的“很经典”吗……

\(\mathscr{F.}\) 「CF 1500D」Tiles for Bathroom

  Link & Submission.

  Tag: 「A.DP-杂项」

  对于 \(k\)，显然可以差分。我们只需要对于 \((i,j)\)，求出以其为右下角的最大合法方阵即可。进一步，可以转化为求 \(q\) 远切比雪夫距离。直接在每个位置维护一个前 \(q\) 近集合，在 \((i,j)\) 合并 \((i-1,j-1),(i-1,j),(i,j-1)\) 的集合并贡献答案。暴躁实现的复杂度是 \(\mathcal O(n^2q\log q)\)。

\(\mathscr{G.}\) 「LOCAL ?」LCM @

  给定序列 \(A=\{a_i\}_{i=1}^n\)，求字典序最小的 \(B=\{b_i\}_{i=1}^n\)，使得 \(\forall i,~b_i\mid a_i\) 且 \(\lcm A=\lcm B\)。

  \(n\le10^4\)，\(a_i\le10^{18}\)。

  显然的贪心：对于每个 \(\lcm A\) 中的 \(p^k\)，把它放在最后一个 \(A\) 中的出现位置。

  素因数分解？这数据范围连 Pollard-Rho 都不放过。考虑从后往前增量法构造 \(B\)。对于当前的 \(i\)，令 \(t\gets a_i\)，枚举 \(j>i\) 并令 \(t\gets t/\gcd(t,b_i)\)，继而得到 \(a_i\) 中取到目前 \(\lcm\) 的素因子集合。把这些素因子幂的乘积作为 \(b_i\)，再将 \(j>i\) 的 \(b_j\) 除掉 \(\gcd(b_i,b_j)\)，因为 \(b_j\) 这一部分素因子的指数不足以贡献 \(\lcm\)，自然是扔掉更优啦。这是一个 \(\mathcal O(n^2\log V)\) 的算法，还是过不了。

  接下来是优化。对于求 \(t\) 的过程，类似 Pollard-Rho，先累积所有 \(b_i\) 再取 \(\gcd\)。令 \(s=\prod_{j>i}b_j\bmod a_i\)，那么 \(s\) 的素因子集是 \(t\) 的超集（但是它们的幂不一定不小于 \(t\) 中的幂）。则不断迭代令 \(t\gets t\gcd(s,a_i),a_i\gets a_i/\gcd(s,a_i)\) 就能得到 \(t\)。这里也许可以优化到单 \(\log\)。

  对于 \(b_j\) 除因子的过程，注意到 \(B\) 是互素的，那么顶多有 \(\log b_i\) 个不同的位置会因除法变化；而一个数最多被除 \(\log\) 次。二分之类的快速找出这些位置除掉 \(\gcd\)。最终可以做到 \(\mathcal O(n^2+n\log n\log V)\)。可能有个 \(\mathcal O(n\log^2V)\)。

  嘴巴真舒服。

\(\mathscr{H.}\) 「洛谷 P6383」Resurrection

  Link & Submission.

  Tags: 「A.DP-树上 DP」「C.性质/结论」

  所以我觉得讨论题真的可能糟蹋了好题。耳朵顺走一个结论啥事没有。

  先来研究 \(G\) 合法的条件。有以下几个必要条件是容易发现的：

  • \(G\) 是树。
  • 以 \(n\) 为根，\(G\) 中结点 \(u\) 的父亲是 \(T\) 中结点 \(u\) 的父亲。
  • \(G\) 中的父子连边在 \(T\) 上对应的路径，若路径共线，则不会交而不含。

  喜闻乐见，这些条件和起来就充分了。

证明

  归纳。\(n=1\) 时成立。设结点数 \(n<k\) 时皆有充分性。尝试证明 \(n=k\) 时的充分性。

  只需要以恰当的方式砍掉一条边就能归纳了。取 \(n\) 在 \(G\) 中的邻接点中，在 \(T\) 中最深的结点 \(u\)。在 \(T\) 上切 \((u,\text{fa}(u))\)，\(G\) 上切 \((u,n)\)。显然，\(G\) 的两个连通块分别对应了 \(T\) 的两个连通块的方案。于是结论成立。  \(\square\)

  对这个结论计数：令 \(f(u,i)\) 表示 \(u\) 选完自己的父亲后，留下了 \(i\) 个严格祖先让孩子们可以选时，\(u\) 子树内的方案数。那么

\[f(u,i)=\prod_{v\in\operatorname{son}(u)}\sum_{j\le i+1}f(v,j). \]

随便优化一下做到 \(\mathcal O(n^2)\)。

\(\mathscr{I.}\) 「CF 1586F」Defender of Childhood Dreams ^

  喏。

\(\mathscr{Summary}\sim6.23\)

\(\mathscr{Contest}~(3/3)\)

  Contest.

  T1 切得比较迅速，顺便醒了瞌睡。T2 想起那啥 \(\gcd\) 矩阵，尝试构造上三角化之类的矩阵构造得脑袋消失。T3 冲了暴力，知道是 DDP 但根本没细想。问题主要是“尝试构造”的过程效率真的低。

\(\mathscr{A.}\) 寄

  给定一棵含 \(n\) 个结点的带权树和 \(m\) 个关键点 \(a_{1..m}\)，选定一个点集 \(b_{1..k}\)，最小化

\[kC+\sum_{i=1}^m\min_{j=1}^k\{\dist(a_i,b_j)\}. \]

  \(n\le3\times10^3\)。

  Tag: 「A.DP-树上 DP」

  最小化最小 \(=\) 最小化任意。每个 \(b\) 可以随意钦定覆盖点，但需要支付覆盖的连通块个数个 \(C\) 的代价。可以证明不会影响最有解的值。于是，令 \(f(u,v)\) 表示钦定 \(u\) 被 \(v\)（任何一个点）覆盖时，\(u\) 子树内的距离与支付的 \(C\) 之和。那么

\[f(u,v)=\sum_{w\in\son(u)}\min\{f(w,v),C+\min_{t}\{f(w,t)\}\}. \]

\(\mathcal O(n^2)\) 很简洁地解决掉。

\(\mathscr{B.}\) 摆 *

  给定 \(n,c\)，构造矩阵 \(A=\{a_{ij}\}\)，其中

\[a_{ij}=\begin{cases} 1, & i=j\\ 0, & i\neq j\land i\mid j\\ c, & \text{otherwise} \end{cases}. \]

求 \(\det A\bmod 998244353\)。

  \(n\le10^{11}\)，\(\text{TL}=6\text s\)。

  Tags: 「A.数学-数学推导」「A.数学-线性代数」「B.Tricks」「C.性质/结论」

  注意到 \(A\) 的主对角线的下方全部是 \(c\)。通过相邻行作差，可以使其成为上海森堡矩阵。每行除一个 \(c-1\)，令 \(v=\frac{c}{c-1}\)，那么现在 \(A\) 长成

\[A=\begin{bmatrix} 1\\ v & 1\\ & v & 1\\ & & \ddots & \ddots\\ & & & v & 1 \end{bmatrix}. \]

（右上部分有值，左下部分全 \(0\)。）注意上海森堡矩阵 \(\det\) 的特殊性，对于其定义式所枚举的 \(\sigma\) 中，每个置换环必然取一堆 \(v\)，最后取一个主对角线及以上的位置。设前 \(i\) 行 \(i\) 列的主子式为 \(f_i\)，那么

\[f_i=f_{i-1}+v\sum_{j\neq i\land j\mid i}f_j-f_{j-1}. \]

令 \(g=\Delta f\)，那么

\[g_i=v\sum_{j\neq i\land j\mid i}g_j. \]

  我们只需要求 \(f_n\)，即 \(g\) 的前缀和。没见过的 trick：这玩意儿可以魔改杜教筛实现的。观察杜教筛的作用式

\[\sum_{i=1}^nt(i)=h(1)S(n)-\sum_{i=2}^nh(i)S(n/i). \]

理论上，\(t,h\) 好求前缀和就行，这并不完全依赖与 \(g\) 的积性。对于本题，构造 \(t(n)=[n=1]v-[n\neq 1]\) 类似物，就能筛了。

  但 \(\mathcal O(n^{2/3})\) 依赖于预处理的线性。注意到 \(g(n)\) 只与 \(\{\alpha_p(n)\}\) 有关，精细地减少对 \(\{\alpha_p(n)\}\) 相同的 \(n\) 的点值计算就能极大地优化速度。复杂度大概就是 \(\mathcal O(n^{2/3})\)。

\(\mathscr{C.}\) 润 *@

  给定函数

\[f(n)=\begin{cases} 0, & n=0\\ 1, & n=1\\ \lceil\log_2n+1\rceil2^{\lceil\log_2n\rceil}+f\left(\lfloor\frac{n}{2}\rfloor\right)+f\left(\lceil\frac{n}{2}\rceil\right), & \text{otherwise} \end{cases}. \]

维护 \(01\) 序列 \(a_{1..n}\)，令 \(v(l,r)=\sum_{i=l}^r2^{i-l}a_i\)，进行 \(q\) 此操作：

  1. \(\forall i\in[l,r],~a_i\gets1-a_i\).
  2. \(\forall i\in[l,r],~a_i\gets0\);
  3. \(\forall i\in[l,r],~a_i\gets1\);
  4. 求出 \(f(v(l,r))\)。

  \(n,q\le10^5\)。

  Tag: 「A.DP-动态 DP」

  可以看出是 DDP。注意这个贡献的转移形式形如 \(\sum k2^{k-1}\rightarrow\sum(k+1)2^k\)，令 \(s=\sum 2^{k-1}\)，\(a=\sum k2^{k-1}\)，就有 \(s'=2s\)，\(a'=2(a+s)\)，构造出了合理的线性变换。

  因此，令 \(\begin{bmatrix}z & o & s & a\end{bmatrix}^T\) 为状态向量。表示考虑了一段前缀，有 \(z\) 种递归末尾进位，\(o\) 中不进位，\(s,a\) 意义如上。分别构造 \(01\) 的转移阵即可。

  不过，对于 \(v(l,r)=2^k\)，\(\log\) 的取整情况会有偏差。所以需要找到后缀 \(00\cdots01\) 的位置，特殊地转移一下。复杂度 \(\mathcal O(q\log n)\) 带 \(4^3\)。

\(\mathscr{Summary}\sim6.24\)

\(\mathscr{Contest}\)

  Contest.

  你感受一下题目名，你说我怎么补。

\(\mathscr{A.}\) tmcpq !

\(\mathscr{B.}\) rsrams !

\(\mathscr{C.}\) hpmo !

\(+.\) 补题/补题解

  • 「AGC 021F」Trinity
  • 「LOCAL 20220616」中学生物理题

\(\mathscr{Summary}\sim6.25\)

\(\mathscr{Class}\rightarrow\) Mathematic Olympics

\(\mathscr{A.}\) 「NOIOL-S 2021」愤怒的小 N

  Link & Submission.

  Tags: 「A.数学-生成函数」「A.数学-数学推导」「B.Tricks」

  一个 trick：

\[a^k=k![x^k]e^{ax}. \]

进一步：

\[\sum_{u\in S}u^k=[x^k]\sum_{u\in S}e^{ux}. \]

  我们令 \(A_t(x),B_t(x)\) 分别为前 \(2^t\) 个位置中，\(\texttt{a},\texttt{b}\) 位置上这个 EGF 的和。那么

\[A_0(x)=1,B_0(x)=0;\\ A_t(x)=A_{t-1}(x)+e^{2^{t-1}x}B_{t-1}(x),\\ B_t(x)=B_{t-1}(x)+e^{2^{t-1}x}A_{t-1}(x). \]

令 \(P_t(x)=A_t(x)+B_t(x)\)，\(Q_t(x)=A_t(x)-B_t(x)\)，这样两个多项式就可以独立递推。那么

\[P_t(x)=\sum_{i=0}^{2^t-1}e^{ix}=\frac{1-e^{2^tx}}{1-e^x},\\ Q_t(x)=Q_{t-1}(x)-e^{2^{t-1}x}Q_{t-1}(x)=\prod_{i=0}^{t-1}(1-e^{2^ix}). \]

  注意到 \([x^0](1-e^{2^tx})=0\)，则 \(k\) 个以上此类多项式的卷积 \([x^k]=0\)。因此 \(Q_t(x)\equiv0\pmod{x^k}~(t\ge k)\)。传统艺能，拿 \(Q_t\) 凑 \(n=(n_{l-1}\cdots n_0)_2\) 的 bit，得到

\[Q(x)=\sum_{i=0}^{l-1}[n_i=1](-1)^{\count((n-({n_i\cdots n_0})_2)}e^{(n-({n_i\cdots n_0})_2)x}Q_i(x). \]

事实上指标 \(i\) 的有效范围只到 \(k\)，直接 \(\mathcal O(k^3)\) 算出来。另一方面 \(P(x)\) 就是个自然数幂和，暴力一个多项式除法就行。最终复杂度是 \(\mathcal O(\log n+k^3)\)，不排除写出 \(\mathcal O(\log n+k^2\log k)\) 的无聊人类。（

\(\mathscr{C.}\) 「BZOJ #4126」国王奇遇记加强版之再加强版

  Link & Submission.

  Tags: 「A.数学-生成函数」「A.数学-数学推导」「A.数学-Langrange 插值」

  \(i^m\)？喜闻乐见，用 \(m![x^m]e^{ix}\) 把 \(m\) 放到指数外。浅推：

\[\begin{aligned} \textit{ans} &= \sum_{i=1}^ni^mm^i\\ &= m![x^m]\sum_{i=1}^ne^{ix}m^i\\ &= m![x^m]\frac{1-m^{n+1}e^{(n+1)x}}{1-me^x}. \end{aligned} \]

其中分母是常多项式，可以分析到答案是关于 \(n+1\) 的多项式。令 \(F(x)=(1-me^x)^{-1}\)，则

\[\textit{ans}=m!f_m-m!m^{n+1}\sum_{i=0}^m\frac{(n+1)^i}{i!}f_{m-i}. \]

可见，若令

\[P(x)=\sum_{i=0}^m\frac{x^if_{m-i}}{i!}, \]

则

\[\textit{ans}=m!P(0)-m!m^{n+1}P(n+1). \]

  但是……我们对 \(P\)，甚至对 \(f\) 一无所知。怎么办？其实 \(n\) 较小的时候，我们可以用答案最初的式子算出来，继而得到若干 \(P(t)\) 与 \(P(0)\) 的值的线性关系。再者，\(P(x)\) 是 \(m\) 次多项式，其 \(m+1\) 阶差分为 \(0\)。所以

\[\Delta^{m+1}P(0)=\sum_{i=0}^{m+1}(-1)^{m+1-i}\binom{m+1}{i}P(i). \]

利用已知线性关系解出 \(P(0)\)，得到点值，Lagrange 差值。线性筛自然数幂、线性求一堆逆元，比较无聊地精细实现可以做到 \(\mathcal O(m)\)。

  PS: 记得判 \(m=1\)，不然 \(F(x)\) 直接戳到分式域里都不知道这么挂的。（

\(\mathscr{D.}\) 「LOJ #6718」九个太阳「弱」化版

  Link.

  一句话题解，求

\[(1+x)^n\bmod (x^K-1) \]

的常数项。可以先用组合意义自行理解。

  关于这垃圾模数：

  「Karatsuba 算法」 设要计算 \(2n-1\) 次多项式 \(F(x)\) 和 \(G(x)\) 的卷积，令 \(F(x)=F_0(x)+x^nF_1(x)\)，\(G(x)=G_0(x)+x^nG_1(x)\)，则

\[\begin{aligned} F(x)G(x) &= (F_0(x)+x^nF_1(x))(G_0(x)+x^nG_1(x))\\ &= F_0(x)G_0(x)+x^n((F_0(x)+F_1(x))(G_0(x)+G_1(x))-F_0(x)G_0(x)-F_1(x)G_1(x))\\ &~~~~+x^{2n}F_1(x)G_1(x). \end{aligned} \]

需要三次卷积，每次卷积递归计算。复杂度 \(T(n)=3T(n/2)+\mathcal O(n)=\mathcal O(n^{\log_23})\)。结束了，不依赖模数。

  没错，它也过不了，你就是得写 MTT。

\(\mathscr{Summary}\sim6.26\)

\(\mathscr{Summary}\sim6.27\)

\(\mathscr{Summary}\sim6.28\)

  前两天摆烂了，顺便发现这篇好像全是 solution set，根本没有 diary，正在考虑开个坑补一下。（

\(\mathscr{Contest}\)

\(\mathscr{A.}\) 基础概率练习题

  已知 \(a_{1..n}\in\mathbb N^n\)，\(a_1\ge k\)，\(\sum a=m\)。随机在 \(\arg\max\{a_i\}\) 中标记一个元素，求这个元素恰好是 \(a_1\) 的概率。答案模 \(998244353\)。

  \(n,m\le10^7\)。

  Tag: 「A.数学-组合计数」

  抛开 \(a_1\ge k\) 的情况下，每个元素成为最大值的概率是均匀的。令 \(R\) 为目标事件，\(A:a_1\ge k\)，\(B:\exist i,~a_i\ge k\)，那么

\[\Pr(R)=\frac{\Pr(B)}{n\Pr(A)}. \]

组合意义不难证明。不过这个构造还是挺巧妙的。随便容斥算一算 \(\mathcal O(n+m)\)。

\(\mathscr{B.}\) 基础树剖练习题

  给定一棵含有 \(n\) 个结点的树，支持 \(q\) 次操作：

  1. 给定 \(u\)，进行从 \(u\) 到根的毛毛虫形修改（具体内容不重要）；
  2. 给定 \(u\)，求 \(u\) 到根的路径答案；
  3. 给定 \(u\)，求 \(u\) 子树内的答案。

  \(n,q\le10^5\)。

  Tag: 「A.树链剖分」

  什么兔会把题意说的那么泛化？因为她整出了个比较泛化的做法。

  最初的手稿放下面，虽然她已经推广了更毒瘤的算法，但这个足够了。

  一些定义：

  • 毛毛虫：一条树上的链和与这条链邻接的所有结点构成的集合；
  • 虫身：毛毛虫的链部分；
  • 虫足：毛毛虫除虫身的部分。

  毛毛虫剖分，是由重链剖分推广而成的，支持 修改/查询 一只毛毛虫的信息，并且可以区分毛毛虫的身体和足分别 修改/查询 不同信息 的树上结点重标号方法。

  由于心情不好，这里直接直接给出重标号方法：

  • 首先重剖求出重链。若现在递归处理到结点 \(u\)：
  • 若 \(u\) 还未被标号，则为其标号；
  • 若 \(u\) 是链头，遍历这条重链，将邻接这条链的结点依次标号；
  • 先递归重儿子，再递归轻儿子。

  此标号方法有如下性质：

  • 对于重链，除链头外的结点标号连续；
  • 对于任意结点，其轻儿子标号连续；
  • 对于以重链头为根的子树，与这条重链邻接的所有结点标号连续；

  所以很方便处理毛毛虫信息。并且，它也能顺便 维护重链链分的所有信息，甚至能够 维护子树的所有信息（一棵子树至多剖分为三个不交区间：重链区间、邻接轻点区间、邻接轻子树区间），复杂度与重链剖分完全一样。

\(\mathscr{C.}\) 基础树论练习题 *@

  称一个有标号有根树合法，当且仅当其所有结点的儿子数量值都属于集合 \(S\)。现用 \(n\) 个结点生成有标号有根森林，重复这一过程 \(k\) 次，对于 \(i\in[1,n]\)，求最终含有 \(nk\) 个结点的森林中，恰好包含 \(ik\) 棵合法树的方案数。答案对 \(p\) 取模。

  \(n\le20\)，\(n<p\le10^5+3\)，\(p\) 为素数，\(k\le10^{16}\)。

  Tags: 「A.数学-组合计数」「A.数学-生成函数」「B.Tricks」

  不难在 \(\mathcal O(\operatorname{poly}(n))\)（甚至指数级）的时间内求出 \(n\) 个结点构成的森林中，关于合法树数量的 OGF \(F(x)\)。现在我们需要求出 \([x^{ik}]F^k(x)\)。

  注意 \(p\) 是任意的，但是范围并不大。利用结论 \(F^p(x)\equiv F(x^p)\pmod p\) 可以进行递归：

\[F^k(x)\equiv F^{k/p}(x^p)F^{k\bmod p}(x)\pmod p. \]

具体来说，假设我们要求 \([x^t]\)，则

\[\begin{aligned}[] [x^t]AB^k &\equiv [x^{pt'+r_t}]AB^{pk'+r_k}\\ &\equiv [x^{pt'+r_t}](AB^{r_k})B^{pk'}\\ &\equiv [x^{pt'+r_t}]x^{r_t}C_{r_t}(x^p)B^{k'}(x^p) & \text{let }AB^{r_k}=\sum_{r=0}^{p-1} x^rC_r(x^p)\\ &\equiv [x^{pt'}]C_{r_t}(x^p)B^{k'}(x^p)\\ &\equiv [x^{t'}]C_{r_t}B & \pmod p \end{aligned} \]

如果预处理出 \(\mathcal O(\log_pk)\) 个 \(C_r\)，就能快速得到答案。也就是说得找到一个模小素数时可行的快速幂方法。可以参照 EI 的博客：整式递推的精度保留问题。

  欲求 \(g=f^k\)，因为我们还得 \(\bmod x^{nk+1}\)，神谕告诉我们若 \(p^2>nk\)，我们可以直接求 \(g\equiv f^k\pmod{p^2}\)，其前 \(p^2\) 项的结果是正确的。自己上去看证明 ✔️

  （天哪，这也太口糊了。）

posted @ 2022-06-14 17:00  Rainybunny  阅读(418)  评论(2)  编辑  收藏  举报