Solution -「NOI 2017」「洛谷 P3826」蔬菜

$\mathscr{Description}$

  Link.

  原题意比较简洁了。注意一下卖出的菜也会变质，且让它们代替未卖出的菜变质是更优的。

$\mathscr{Solution}$

  一眼网络流，尝试建图。在原题意上建图的话我得到了一个五层结点的图……于是可以以逆向时间描述问题。不难得到模型：

• $S$ 连向 $(i,t)$，容量为菜 $i$ 在 $t$ 时刻变质的数量，费用为 $a_i$；若 $t$ 时刻后 $i$ 全部变质，则分出一单位流量增加 $s_i$ 的费用。
• $(i,t)$ 连向 $(i,t-1)$，容量为 $+\infty$，费用为 $0$；
• $(i,t)$ 连向 $T_t$，容量为 $+\infty$，费用为 $0$；
• $T_t$ 连向 $T$，容量为 $m$，费用为 $0$。

  对于单个询问，该图的最大费用任意流（其实必然是最大流）费用就是答案。直接来貌似可以获得比较可观的分数。

  接下来，我们手动分析流网络，通过比较模式化的分析找到结论。

  考虑按（正向）时间顺序加入 $T_t$ 及其连边的过程，从增广的角度思考答案的更新：

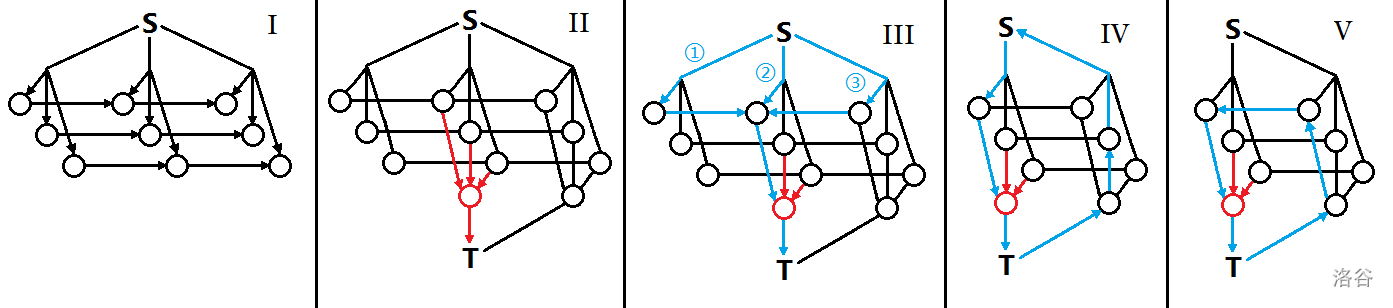
  图中 IV 的增广环不如仅走右侧蓝色路径的反向路径优秀；V 的增广环显然不是负环。因此，$S$ 无法在残余网络上推流。回归到原问题，得到结论：当 $t_1>t_2$，$t_2$ 所选择的蔬菜集合是 $t_1$ 的子集。如果我们求出 $t_\max$，贪心地去掉最便宜的菜就能得到其他时刻的答案。

  求 $t_\max$ 的答案？类似地分析可以发现，随着时间（逆向）向前，每种蔬菜的选取数量都会越来越多。因而可以维护现有蔬菜的堆，以及可能因为 $S$ 的流量进入“复活”的蔬菜集合。模拟 $T_t$ 从大到小向 $T$ 增广的过程即可。

  复杂度 $\mathcal O(nm\log n)$。

$\mathscr{Code}$

/*+Rainybunny+*/

#include <bits/stdc++.h>

#define rep(i, l, r) for (int i = l, rep##i = r; i <= rep##i; ++i)
#define per(i, r, l) for (int i = r, per##i = l; i >= per##i; --i)

typedef long long LL;
typedef std::pair<int, int> PII;
#define fi first
#define se second

template <typename Tp>
inline void chkmin(Tp& u, const Tp& v) { v < u && (u = v, 0); }
template <typename Tp>
inline void chkmax(Tp& u, const Tp& v) { u < v && (u = v, 0); }
template <typename Tp>
inline Tp imin(const Tp& u, const Tp& v) { return u < v ? u : v; }
template <typename Tp>
inline Tp imax(const Tp& u, const Tp& v) { return u < v ? v : u; }

const int MAXN = 1e5, MAXM = 10;
int n, m, k, a[MAXN + 5], s[MAXN + 5], c[MAXN + 5], x[MAXN + 5], p[MAXN + 5];
int sold[MAXN + 5], wait[MAXN + 5];
LL ans[MAXN * MAXM + 5];
std::vector<int> imp[MAXN + 5];

int main() {
    scanf("%d %d %d", &n, &m, &k);
    rep (i, 1, n) scanf("%d %d %d %d", &a[i], &s[i], &c[i], &x[i]);
    rep (i, 1, k) scanf("%d", &p[i]);

    int mxt = *std::max_element(p + 1, p + k + 1);
    rep (i, 1, n) {
        if (!x[i]) imp[mxt].push_back(i);
        else imp[imin(mxt, (c[i] + x[i] - 1) / x[i])].push_back(i);
    }

    std::priority_queue<PII> heap;
    per (i, mxt, 1) {
        for (int j: imp[i]) wait[++wait[0]] = j;
        rep (i, 1, wait[0]) {
            heap.emplace(sold[wait[i]] ? a[wait[i]]
              : a[wait[i]] + s[wait[i]], wait[i]);
        }
        wait[0] = 0;
        for (int rst = m; rst-- && !heap.empty();) {
            int u = heap.top().se;
            ++sold[u], heap.pop();
            if (c[u] - (i - 1) * x[u] > sold[u]) heap.emplace(a[u], u);
            else if (x[u]) wait[++wait[0]] = u;
        }
    }

    rep (i, 1, n) if (sold[i]) {
        ans[++ans[0]] = a[i] + s[i];
        while (--sold[i]) ans[++ans[0]] = a[i];
    }
    std::sort(ans + 1, ans + ans[0] + 1);
    std::reverse(ans + 1, ans + ans[0] + 1);
    rep (i, 2, ans[0]) ans[i] += ans[i - 1];
    int all = ans[0]; ans[0] = 0;
    rep (i, 1, k) printf("%lld\n", ans[imin(all, p[i] * m)]);
    return 0;
}