Solution Set - 《赏竹而格之》
- 1 「GXOI / GZOI 2019」「洛谷 P5304」旅行者
- 2 「SDOI 2019」「洛谷 P5361」热闹的聚会与尴尬的聚会
- 3 「LibreOJ NOI Round #1」「LOJ #508」失控的未来交通工具
- 4 「FJOI 2018」「洛谷 P4577」领导集团问题
- 5 「SHOI 2012」「洛谷 P3830」随机树
- 6 「CEOI 2020」「洛谷 P6517」Alliances
- 7 「CF 914F」Substrings in a String
- 8 「BZOJ 3569」DZY Loves Chinese II *🔯
- 9 「SP 16549」QTREE6 - Query on a tree VI +*
- 10 「CF 1284D」New Year and Conference
- 11 「SCOI 2013」「洛谷 P3281」数数
- 12 「JSOI 2016」「洛谷 P4322」最佳团体
- 13 「LOJ #6538」烷基计数 加强版 加强版 +
- 14 「JSOI 2018」「洛谷 P4516」潜入行动
- 15 「HAOI 2010」「洛谷 P2515」软件安装
- 16 「PKUWC 2018」「洛谷 P5298」Minimax 🔯
- 17 「ZJOI 2018」「洛谷 P4338」历史 +🔯
- 18 「CF 1146F」Leaf Partition
- 19 「CF 1140G」Double Tree
- 20 「OurOJ #9139」Calc +*
- 21 「CF 1207G」Indie Album
- 22 「SCOI 2012」「洛谷 P2336」喵星球上的点名
- 23 「NOI 2015」「洛谷 P2150」寿司晚宴
- 24 「洛谷 P1357」花园
- 25 「CTSC 2017」「洛谷 P3771」网络 *
- 26 「SCOI 2008」「洛谷 P2474」天平
- 27 「USACO 2013 OPEN」「洛谷 P3084」Photo G
- 28 「JSOI 2019」「洛谷 P5332」精准预测
- 29 「洛谷 P5212」SubString
- 30 「WC 2013」「洛谷 P4074」糖果公园
- 31 「SDOI 2017」「洛谷 P3783」天才黑客
- 32 「ZJOI 2010」「洛谷 P2570」贪吃的老鼠 *🔯
标题后的 + 表示不在某题单中,* 表示我成为了题解屑,🔯 表示神题。
1 「GXOI / GZOI 2019」「洛谷 P5304」旅行者
Link & Submission.
Tags: 「A.图论-最短路相关」「B.Tricks」
经典二进制分组,没啥好说的。
2 「SDOI 2019」「洛谷 P5361」热闹的聚会与尴尬的聚会
Link & Submission.
Tags: 「A.随机化」「C."NPC"」
随便拓扑一发可以求到最大的 \(p\),进而得到 \(q\) 的目标值。我一看,精确求 \(q\) 是 NP-Hard?!好的我们 std::shuffle 一发依次选……我焯它过了?
确定性算法:注意到 \((p+1)(q+1)\ge n+1\),我们每次取 \(\arg\min\{d(u)\}\),将它和它的邻接点删掉,尝试构造独立集,同时用当前的 \(\min\{d(u)\}\) 和对应的图更新 \(q\) 度图,然后发现可行√
如果实现随意都是 \(\mathcal O(Tm\log m)\) 的。
3 「LibreOJ NOI Round #1」「LOJ #508」失控的未来交通工具
Link & Submission.
Tags: 「A.并查集」「A.数学-数论」「C.性质/结论」
我卡得比较久的地方是第一步转化的先入为主:觉得这个和同余最短路相关,继而想动态维护最短路之类的鬼东西……
图非常不可做,一般我们选择将路径特殊化:变成树边 + 环,但恼人的是这个“环”似乎并不独立于“路径”,我们必须先走到环上的点才能进入环。联系经典的异或路径问题,可以尝试一步构造,让环仅依赖于连通块存在:若想要加入一个环,我们从路径上一点从任意路径走向环,绕一圈,然后在这“任意路径”上往返 \(m\) 次即可。显然我们只需要关心所有环长的 \(\gcd\),并查集记录这一信息。
对于询问,可以转化成求 \(gx+my=\cdots\) 的整数解问题,虽然数学计算的 corner cases 很多但写题解就不重要了√ 复杂度是 \(\mathcal O(q\log V)\)。
4 「FJOI 2018」「洛谷 P4577」领导集团问题
Link & Submission.
Tag:「C.性质/结论」
经典题,类似 LIS 的三种求法的灵活运用。略了。
5 「SHOI 2012」「洛谷 P3830」随机树
Link & Submission.
Tag: 「A.DP-概率/期望 DP」
概率期望 DP 入门。先求 \(p(i,j)\) 表示在子树内操作 \(i+j+1\) 次(根必然操作一次),使得根的左子树内被操作 \(i\) 次,右子树内被操作 \(j\) 次的概率。两个问题都能用超级 naive 的朴素 DP 过掉,没错,\(\mathcal O(n^4)\) 那种都行。
6 「CEOI 2020」「洛谷 P6517」Alliances
Link & Submission.
Tag: 「A.图论-网络流-最大流/最小割」
无限之环超级弱化版。显然可以网格图二染色建图跑网络流,对于人类村庄拆成一个纵向连边和一个横向连边的 \(1\) 流量的点就行。复杂度 \(\mathcal O(\operatorname{Dinic}(2n^2+2,4n^2))\),这个是严格二分图所以应该有个 \(\mathcal O(n^3)\) 的上界?
7 「CF 914F」Substrings in a String
Link & Submission.
Tags: 「A.分块」「B.std::bitset」
当出题人开出 \(6\text s\) 时限时,本题不再甄别先手水平,仅仅考察选手的情商。(
好的我们 \(\mathcal O(\frac{nq}{\omega})\) 先把题过掉,然后想想正解。
注意那个 \(\sum|y|\) 的限制也自带一个根号:超过 \(\sqrt n\) 的 \(y\) 可以暴力。对于小于 \(\sqrt n\),可以在原串上根号分块求整块贡献,散块也可以暴力做,总之就是 \(\mathcal O(n\sqrt n)\)(所有东西同阶)。
8 「BZOJ 3569」DZY Loves Chinese II *🔯
Link & Submission.
Tags: 「A.图论-生成树」「C.思维」「C.性质/结论」
一贯套路,取一棵 DFS 树,考虑树边和非树边的删除情况,设覆盖树边 \(e\) 的非树边构成集合 \(S_e\),对于非树边 \(e\) 令 \(S_e=\{e\}\),有结论:
删去边集 \(P\) 后图不连通,当且仅当 \(\exist \varnothing\neq Q\subseteq P,~{\large\Delta}_{e\in Q}S_e=\varnothing\)。(\(\Delta\) 是对称差,即集合异或。)
证明
仅对一个极小的边集 $Q$ 证明即可。
必要性:$Q$ 是割。由于 $Q$ 极小,所以 $Q$ 这个割应将图划分为恰好两个连通块。在 DFS 树上考虑这个连通块,忽略其内部连边缩成一个点,形如:
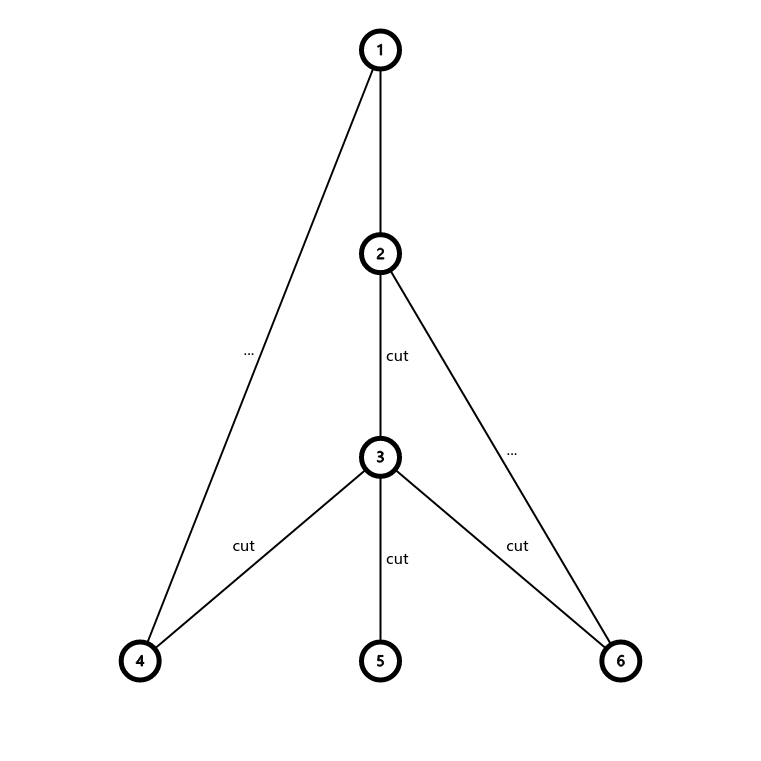
($(3,5)$ 不该 cut,手误 qwq。)其中结点 $3$ 即被割掉的连通块。那么根据极小性和不连通的条件,$3$ 子树内的每条未被割的返祖边必须连向 $3$ 的严格祖先,所以每条这样的返祖边都在两个 $S_e$ 中出现;属于 $Q$ 的返祖边类似。于是 $Q$ 内 $S$ 的对称差为 $\varnothing$。
充分性:${\large\Delta}_{e\in Q}S_e=\varnothing$。显然至少有一条树边 $e_0\in Q$,所以仅考虑生成树,将所有 $Q$ 内的树边割掉时,树会变为若干个连通块。将连通块视为结点,那么割掉的树边又能将这些结点连成一棵新树。在新树上对结点黑白染色,注意到对于任意不在 $Q$ 中的非树边 $e_1$,一定存在与偶数个 $S_e$ 中,对应到新树上,它就必然连接两个同色的结点。因此,黑色结点集合与白色结点集合不可能有边相连,所以 $Q$ 是割。 $\square$
有这个结论之后就比较简单了:将每条非树边随机映到 \(\{0,1\}^{64}\),集合 \(S_e\) 变为集合内非树边映射值的异或。询问时,判断删除边集构成的向量集是否线性相关即可。复杂度 \(\mathcal O(m+64q)\)。正确率显然很高。(
9 「SP 16549」QTREE6 - Query on a tree VI +*
Link & Submission.
Tags: 「A.数据结构-LCT」「B.Tricks」
LCT 维护子树?哦这个不就是 DDP 那种更新方法嘛……欸那我点开题解干嘛。
容易想到用 LCT 大力维护黑白连通块,但是 LCT 是以连边断边为基本操作的,所以我们得把点的黑白变化转化成常数条边的黑白变化。
第一个想法就是确定原树的根,把点权给到父亲边权上。LCT 精细实现,不借助 make-root 实现父子连边断边,查询 \(u\) 时 access 上去去掉连通块根的虚子树贡献即可,注意要给原树根也弄个爹。复杂度是 \(\text{LCT}-\mathcal O(n\log n)\)(即十几倍常数的单 log)。
LCT 维护子树:每个结点维护父亲指向它的虚儿子的子树和。
10 「CF 1284D」New Year and Conference
Link & Submission.
Tag: 「B.Hash」
赛上做法:扫描线 + 线段树,挺无脑的。
现在我并没有发现以前做过所以再来一次 qwq。给每个会议随机一个权值,检查每个会议在两个会场中不产生矛盾的会议集合是否相同即可。还是 \(\mathcal O(n\log n)\) 的(离散化)。
11 「SCOI 2013」「洛谷 P3281」数数
Link & Submission.
Tags: 「A.DP-数位 DP」「C.细节」
什么逝娘题啊……维护前缀答案(顶满/没顶满上界),前缀的后缀贡献和(顶满/没有顶满上界),前缀没顶满的方案数,前缀能够给下一个位置贡献的后缀数量,用耐心催化使之 AC。复杂度 \(\mathcal O(n+m)\)。
12 「JSOI 2016」「洛谷 P4322」最佳团体
Link & Submission.
Tags: 「A.DP-树上 DP」「A.二分-二分答案」
分数规划 + 树上背包,\(\mathcal O(n^2\log\frac{V}{\epsilon})\) 没啥好说的。
13 「LOJ #6538」烷基计数 加强版 加强版 +
14 「JSOI 2018」「洛谷 P4516」潜入行动
Link & Submission.
Tag: 「A.DP-树上 DP」
大家都会叭,简单说明一下背包复杂度上界。对于极大的大小不超过 \(m\) 的子树,最多提供 \(\mathcal O(m^2)\) 的复杂度,最多 \(\mathcal O(n/m)\) 棵,这部分是 \(\mathcal O(nm)\);对于大小超过 \(m\) 的子树,可以将其视为二叉树的背包合并,每个结点的背包都为 \(\mathcal O(m^2)\),这棵大二叉树的每个叶子是上一个部分的极大子树,所以最多 \(\mathcal O(n/m)\) 个叶子做二叉合并,那么最多和这么多次,这部分也是 \(\mathcal O(nm)\),所以总共复杂度 \(\mathcal O(nm)\)。
你要说这个“\(\mathcal O(nm^2)\) 暴力背包”一看常数就很小也没什么问题。(
15 「HAOI 2010」「洛谷 P2515」软件安装
Link & Submission.
Tags: 「A.DP-树上 DP」「A.图论-缩点/圆方树」
这题真没闪光点,重视基础也要有个度吧 qwq。(碎碎念.jpg
16 「PKUWC 2018」「洛谷 P5298」Minimax 🔯
17 「ZJOI 2018」「洛谷 P4338」历史 +🔯
18 「CF 1146F」Leaf Partition
Link & Submission.
Tag: 「A.DP-树上 DP」
令 \(f(u,0/1/2)\) 表示 \(u\) 子树内,\(u\) 不属于叶子连通块 / \(u\) 属于叶子连通块且 \(u\) 处没拐弯 / \(u\) 属于叶子连通块且 \(u\) 处拐过弯 的方案数。转移不难,复杂度 \(\mathcal O(n)\)。
19 「CF 1140G」Double Tree
Link & Submission.
Tags: 「A.树论-点分治/点分树」「A.图论-最短路相关」「B.贪心」
我又把难点一眼秒了,却被不是难点的地方卡住了(?
不妨记 \(u_0=2u-1\),\(u_1=2u\)。考虑若求出了 \(w(u)=\operatorname{dist}(u_k,u_{1-k})\),就可以随便点分离线求答案(貌似也可以倍增)。对于 \(w\),联系图的形式,发现 \(u_0\) 走到 \(u_1\) 的路径一定形如:从 \(u_0\) 在 \(0\) 结点树向上爬到 \(x_0\),从 \(x_0\) 切换到 \(x_1\),再从 \(x_1\) 在 \(1\) 结点树向下爬到 \(u_1\);或者先向下爬,切换,再爬回来。因为边权非负,所以最短路本身是具有贪心性质的,随便选一个根,DFS 两次,第一次用儿子更新父亲,第二次用父亲更新儿子,这样就能描述出上述两种路径了。
提醒一下,这种先儿子更新父亲,再父亲更新儿子的 trick 经常用于树形最短路,例如世界树也有这个 trick 的参与。
总共复杂度是 \(\mathcal O(n\log n)\)。
20 「OurOJ #9139」Calc +*
Tags: 「A.数学-Lagrange 插值」「C.性质/结论」
拉插忘得差不多了,我谢罪。
显然可以仅计数 \(\{a_n\}\) 升序的情况,那么有个 naive 的 DP:令 \(f(i,j)\) 表示选了 \(i\) 个数,考虑了 \(1..j\) 时的所有方案乘积之和,那么
根据上文的提示(其实更应该根据观察和经验啦),有
设 \(f(i-1,j-1)\) 是关于 \(j\) 的 \(d\) 次函数,那么 \(\Delta f(i,j)\) 是 \(d+1\) 次,\(f(i,j)\) 是 \(d+2\) 次,最终有 \(f(n,A)\) 是 \(2n\) 次,预处理几个点值拉插即可。虽然拉插式子里分母有可能模出来为 \(0\),但是这个 \(f\) 函数是客观存在的,所以我们只需要断言 \(0\) 会被约掉就好。复杂度粗暴实现是 \(\mathcal O(n^2)\) 的。
21 「CF 1207G」Indie Album
Link & Submission.
Tags: 「A.字符串-ACAM」「B.DFN」
小心!询问串才是模式串,给它们整个 AC 自动机,那么前面 \(n\) 个操作就是 ACAM 上的遍历,DFS 这一遍历过程,每个点的答案是:当前 DFS 栈所有结点中,在 fail 树上是询问串后代的数量。BIT 动态维护栈中结点即可。
然后有只傻兔子拿持久化线段树维护了 DFS + BIT 的过程,正所谓族庖月更刀,粪也。😅
22 「SCOI 2012」「洛谷 P2336」喵星球上的点名
Link & Submission.
Tags: 「A.莫队-一般莫队」「A.字符串-SA」
挺有训练意义的一道题。方便起见,把姓名串加分隔符拼到一起。考虑一个点名串 \(t\),它以子串出现的起始位置自然是很离散的,而一只猫猫被点名,当且仅当它的姓名对应的下标内,存在一个 \(t\) 的起始位置,这反而是连续的……
于是想到,可以借助 SA 将“出现位置”转化成区间,将“下标属于哪只猫猫”作为颜色,发现这就是经典莫队问题。对于第二类询问,莫队更新时给出现状态发生变化的猫猫打差分标记即可。
拼出来的字符串长度是 \(L_1=2n+\sum|\textit{name}|\),我求“转化成区间”这一步直接拿询问串在 SA 序列上暴力二分,记 \(L_2=\sum|\textit{query}|\),那么复杂度是 \(\mathcal O((L_1+L_2)\log L_1+q\sqrt L_1)\)。随便冲一发就最优解也是我没想到的。😺
还有啊,为什么我每次写 SA 都要琢磨半天,每次重新构思算法,根本背不住 qwq……
23 「NOI 2015」「洛谷 P2150」寿司晚宴
Link & Submission.
Tags: 「A.DP-计数 DP」「B.Tricks」
见过一次的 trick,做这题的时候一步一步从踩标复杂度伪成正解复杂度 qwq。
显然我们仅需关心小 G 和小 W 手里的素因子,顺手求一下 \(\pi(n)\),很大?再顺手求一下 \(\pi(\sqrt n)\)?欸果然很小,也就是说最大素因子不超过 \(\sqrt n\) 的数我们可以随便状压;最大素因子超过 \(\sqrt n\) 的数呢?因为一个数最多含有一个这样的因子,我们按照这个因子把数归类,每一类里记一个小 G 小 W 手里有没有当前这个大素因子的 0/1/2 状态即可。复杂度丑陋实现可以做到 \(\mathcal O(n3^{\pi(\sqrt n)})\)。
24 「洛谷 P1357」花园
Link & Submission.
Tag: 「B.向量/矩阵优化」
复杂度 \(\mathcal O((2^m)^3\log n)\),你说怎么做。
25 「CTSC 2017」「洛谷 P3771」网络 *
Link & Submission.
Tags: 「A.分治-二分答案」「B.Tricks」「C.性质/结论」
哈哈哈哈沉迷分讨没注意到绝对值能拆。
显然边连在直径上,令 \(a_u\) 表示直径上 \(u\) 点直径外子树的高度,\(s_u\) 表示 \(u\) 到直径一端的距离,转化成序列问题。发现直接来真的很麻烦,尝试套一个二分。设当前二分答案 \(D\),康康边连在 \(p,q~(p\le q)\) 的合法条件:
我觉得其实这一步才是本题难点,你需要很意识流地把 \(a_u-s_u\le D-a_v-s_v\) 这个不用 \(L\) 边的平凡条件拿出来手动否定掉,再考虑非平凡条件。接下来比较讨论,爆拆绝对值:
注意 \((u,v)\) 和 \((p,q)\) 没啥关系,而 \(u,v\) 是 \(\forall\) 声明下的,所以可以最大化 / 最小化与 \((u,v)\) 相关的取值,再来考虑有没有满足条件的 \(p,q\)。前者 BIT 维护,后者 four-pointers (?) 即可。复杂度 \(\mathcal O(n\log n\log V)\)。
洛谷这篇题解的“单调队列求 \(u,v\) 最大化 / 最小化”那里没看懂?啥玩意儿单调呐?
26 「SCOI 2008」「洛谷 P2474」天平
Link & Submission.
Tag: 「A.图论-差分约束」
差分约束可以求出两个变量 \(x_i,x_j\) 间 \(x_i-x_j\) 的最大值(是上界,求最短路)和最小值(是下界,求最长路)。枚举天平另一端的 \(i,j\),讨论 \(x_i-x_A\),\(x_j-x_B\),……的取值即可。复杂度 \(\mathcal O(n^3)\)。
27 「USACO 2013 OPEN」「洛谷 P3084」Photo G
Link & Submission.
Tag: 「A.图论-差分约束」
可以比较无脑地扔上去一个差分约束 SPFA?跑不过。SLF+swap 优化也只有 \(90\)?我们点开题解,看到个梦想 SPFA?新科技我学……我你妈松弛 \(19260817\) 次之后直接判无解就过了。😅
正解是 DP,兔子不喜欢.jpg
28 「JSOI 2019」「洛谷 P5332」精准预测
Link & Submission.
Tags: 「A.图论-2_SAT」「A.分块」「B.std::bitset」「C.细节」
读对题:对于活到最后的 \(u\),求有多少个 \(v\) ……并不需要这些 \(v\) 同时活着。
显然 2-SAT,建一发图,搞个 DAG,std::bitset 暴力维护一下每个点能到的 F 点以及可以选 T 的人,用这两个 bitset 就能算答案。
但这个空间有点 😅,分个块儿,每次只考虑块内的上述信息即可。
时间 \(\mathcal O(\frac{nm+nB^2}{\omega})\),空间 \(\mathcal O(mB)\)。
29 「洛谷 P5212」SubString
Link & Submission.
Tags: 「A.数据结构-LCT」「A.字符串-SAM」
动态维护出现次数?可以想到 SAM。对于询问,一路转移到询问串对应的结点 \(u\),那么 \(u\) 在 fail 树子树内的非虚点数量即为答案。可惜 SAM 在不断更新,fail 树在被 link cut,所以我们写一个不需要 make-root 的 LCT 维护 fail 树子树和就行。复杂度 \(\mathcal O(\sum|S|+q\log\sum|S|)\),LCT 的 \(\log\)。
30 「WC 2013」「洛谷 P4074」糖果公园
Link & Submission.
Tags: 「A.莫队-树上莫队」「A.莫队-带修莫队」
题如其 tag。
31 「SDOI 2017」「洛谷 P3783」天才黑客
Link & Submission.
Tags: 「A.树论-虚树」「A.图论-最短路相关」「B.优化建图」「C.细节」
显然我们应该从边的角度考虑“距离”,令 \(\operatorname{dist}(e)\) 表示走过边 \(e\) 的最小花费,问题在于边作为“点”,实际的点对应了“点”的完全图关系,我们不可能暴力地建图跑最短路。
注意 Trie 树都给你了,把一个结点的邻接边挂到虚树上,从子树的角度,对跨过 LCA 的所有结点互相两边,这样就能前后缀优化建图了。注意自环是有可能有用的,不要忽略。最终有 \(\mathcal O(m)\) 条边(带大概 \(18\) 倍常数),总之就是 \(\mathcal O(m\log m)\) 的。
看吧,口胡确实很爽。但是 6K 实在狗屎,而且貌似跟别人建图方法不尽相同 qwq。
32 「ZJOI 2010」「洛谷 P2570」贪吃的老鼠 *🔯
既然 32 是个不大也不小的 \(2\) 的幂,那么本篇 Solution Set 就到这里叭,挂到明天取消置顶 awa~
(既然如此,下次从 \(0\) 编号到 \(31\) 才舒服点。)

