Solution -「洛谷 P5236」「模板」静态仙人掌
Link.
给定一个 个点 条边的仙人掌, 组询问两点最短路。
,。
提出一个环来考虑,从环上一点 到 ,无非两条路径。可以按顺序处理一个前缀和。如图:
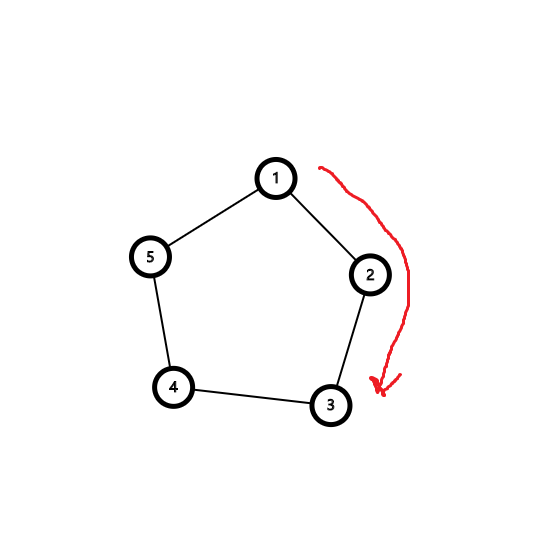
令 为结点 到 的顺时针距离, 为结点 到 的顺时针距离……特别地, 记录整个环的大小。那么环上 和 的最短距离就是 。这样就能 求到了。
接下来建圆方树(很多题解说建树的细节与普通图不一样,其实正常建也没有任何问题 qwq),发现一个圆点走进方点(点双),在走到父亲圆点的最短距离可以在 算法中预处理出来。考虑圆方树上的边权:圆点到父亲方点的边权为上述最短距离,否则为 。对于询问 ,找到其 (设为 ),分 的情况讨论:
- 是圆点,那么 时求出的树上距离就是答案。
- 是方点,此时树上距离实际上是 和 走到 的父亲圆点的距离之和,明显时错误的—— 和 走进同一个点双后,需要求一次最短距离而非直接在父亲会和。所以可以倍增求到 走进点双的第一个点(即方点向 点方向的儿子圆点),同理求出 ,利用处理的前缀和求到 到 的最短距离。那么答案就是 。
复杂度 。不过这里作者偷懒用 std::map 记录了每个环的 ,写得好看一点是可以在这一部分做到 。但求走进点双的第一个点似乎必须用带 的算法 owo?
#include <map>
#include <cstdio>
#include <algorithm>
#define adj( g, u, v, c ) \
for ( int eid = g.head[u], v, c; v = g.to[eid], c = g.cst[eid], eid; eid = g.nxt[eid] )
const int MAXN = 2e4, MAXM = 4e4;
int n, m, q, snode, fa[MAXN + 5][15];
int dfc, top, dfn[MAXN + 5], low[MAXN + 5], stk[MAXN + 5];
int dep[MAXN + 5], dis[MAXN + 5], root[MAXN + 5];
std::map<int, int> sum[MAXN + 5];
struct Graph {
int ecnt, head[MAXN + 5], to[MAXM + 5], cst[MAXM + 5], nxt[MAXM + 5];
inline void link ( const int s, const int t, const int c ) {
to[++ ecnt] = t, cst[ecnt] = c, nxt[ecnt] = head[s];
head[s] = ecnt;
}
inline void add ( const int u, const int v, const int c ) {
link ( u, v, c ), link ( v, u, c );
}
} src, tre;
inline char fgc () {
static char buf[1 << 17], *p = buf, *q = buf;
return p == q && ( q = buf + fread ( p = buf, 1, 1 << 17, stdin ), p == q ) ? EOF : *p ++;
}
inline int rint () {
int x = 0; char s = fgc ();
for ( ; s < '0' || '9' < s; s = fgc () );
for ( ; '0' <= s && s <= '9'; s = fgc () ) x = x * 10 + ( s ^ '0' );
return x;
}
inline void wint ( const int x ) {
if ( 9 < x ) wint ( x / 10 );
putchar ( x % 10 ^ '0' );
}
inline int min_ ( const int a, const int b ) { return a < b ? a : b; }
inline bool chkmin ( int& a, const int b ) { return b < a ? a = b, true : false; }
inline bool chkmax ( int& a, const int b ) { return a < b ? a = b, true : false; }
inline int cost ( const Graph& g, const int s, const int t ) {
adj ( g, s, u, c ) if ( u == t ) return c;
return -1;
}
inline int mncost ( const int id, int u, int v ) {
int t1 = sum[id][u], t2 = sum[id][v];
if ( t1 > t2 ) t1 ^= t2 ^= t1 ^= t2;
return min_ ( t2 - t1, sum[id][root[id]] - ( t2 - t1 ) );
}
inline void buildSquare ( const int rt, const int p, const int sid ) {
int beg = top; for ( ; stk[beg] ^ p; -- beg );
root[sid] = rt;
// loop: rt - stk[beg] - stk[beg + 1] - ... - stk[top] - rt.
for ( int i = beg, cur = p, pre = rt; i <= top; pre = cur, cur = stk[++ i] ) {
sum[sid][cur] = sum[sid][pre] + cost ( src, pre, cur );
}
sum[sid][rt] = sum[sid][stk[top]] + cost ( src, stk[top], rt );
int u;
do {
u = stk[top --];
tre.add ( sid, u, mncost ( sid, rt, u ) );
} while ( u ^ p );
}
inline void Tarjan ( const int u, const int fa ) {
dfn[u] = low[u] = ++ dfc, stk[++ top] = u;
adj ( src, u, v, c ) if ( v ^ fa ) {
if ( ! dfn[v] ) {
Tarjan ( v, u ), chkmin ( low[u], low[v] );
if ( low[v] >= dfn[u] ) {
tre.add ( u, ++ snode, 0 );
buildSquare ( u, v, snode );
}
} else chkmin ( low[u], dfn[v] );
}
}
inline void init ( const int u, const int f ) {
dep[u] = dep[fa[u][0] = f] + 1;
for ( int i = 1; i <= 14; ++ i ) fa[u][i] = fa[fa[u][i - 1]][i - 1];
adj ( tre, u, v, c ) if ( v ^ f ) {
dis[v] = dis[u] + c;
init ( v, u );
}
}
inline int calcLCA ( int u, int v ) {
if ( dep[u] < dep[v] ) u ^= v ^= u ^= v;
for ( int i = 14; ~ i; -- i ) if ( dep[fa[u][i]] >= dep[v] ) u = fa[u][i];
if ( u == v ) return u;
for ( int i = 14; ~ i; -- i ) if ( fa[u][i] ^ fa[v][i] ) u = fa[u][i], v = fa[v][i];
return fa[u][0];
}
inline int climb ( int u, const int tar ) {
for ( int i = 14; ~ i; -- i ) if ( dep[fa[u][i]] > dep[tar] ) u = fa[u][i];
return u;
}
int main () {
n = snode = rint (), m = rint (), q = rint ();
for ( int i = 1, u, v, w; i <= m; ++ i ) {
u = rint (), v = rint (), w = rint ();
src.add ( u, v, w );
}
Tarjan ( 1, 0 );
init ( 1, 0 );
for ( int u, v; q --; ) {
u = rint (), v = rint ();
int w = calcLCA ( u, v );
if ( w <= n ) wint ( dis[u] + dis[v] - 2 * dis[w] );
else {
int pu = climb ( u, w ), pv = climb ( v, w );
wint ( dis[u] - dis[pu] + dis[v] - dis[pv] + mncost ( w, pu, pv ) );
}
putchar ( '\n' );
}
return 0;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现