Note -「多项式」基础模板（FFT/NTT/多模 NTT）光速入门

  进阶篇戳这里。

目录

• \(\omega\) 何为「多项式」\(\omega\)
  • \(\omega\) 基本概念 \(\omega\)
  • \(\omega\) 系数表示法 & 点值表示法 \(\omega\)
• \(\omega\) 傅里叶（Fourier）变换 \(\omega\)
  • \(\omega\) 概述 \(\omega\)
  • \(\omega\) 前置知识 - 复数 \(\omega\)
  • \(\omega\) 单位根 \(\omega\)
  • \(\omega\) 快速傅里叶正变换（FFT）\(\omega\)
  • \(\omega\) 快速傅里叶逆变换（IFFT）\(\omega\)
  • \(\omega\) 迭代实现 \(\omega\)
  • \(\omega\) 例题 \(\omega\)
    • \(\omega\)「洛谷 P3803」「模板」多项式乘法（FFT）\(\omega\)
      • \(\omega\) 题意简述 \(\omega\)
      • \(\omega\) 数据规模 \(\omega\)
      • \(\omega\) \(\text{Solution}\) \(\omega\)
      • \(\omega\) \(\text{Code}\) \(\omega\)
• \(\omega\) 快速数论变换（NTT）\(\omega\)
  • \(\omega\) 原根 \(\omega\)
  • \(\omega\) 实现 \(\omega\)
  • \(\omega\) NTT 模数 \(\omega\)
  • \(\omega\) 奇怪的模数 - 任意模数 NTT \(\omega\)
    • \(\omega\) 三模 NTT \(\omega\)
    • \(\omega\) 拆系数 FFT（MTT）\(\omega\)
      • \(\omega\) 七次转五次 \(\omega\)
      • \(\omega\) 五次转四次 \(\omega\)
  • \(\omega\) 例题 \(\omega\)
    • \(\omega\) 「洛谷 P4245」「模板」任意模数 NTT
      • \(\omega\) 题意简述 \(\omega\)
      • \(\omega\) 数据规模 \(\omega\)
      • \(\omega\) \(\text{Solution}\) \(\omega\)
      • \(\omega\) \(\text{Code}\) \(\omega\)
    • \(\omega\) 「CF 623E」Transforming Sequence \(\omega\)
      • \(\omega\) 题意简述 \(\omega\)
      • \(\omega\) 数据规模 \(\omega\)
      • \(\omega\) \(\text{Solution}\) \(\omega\)
• \(\omega\) 参考资料 \(\omega\)

\(\omega\) 何为「多项式」\(\omega\)

  多项式（polynomial）是指由变量（variable）、系数（coefficient）以及它们之间的加、减、乘、幂运算（非负整数次方）得到的表达式。多项式就是整式。

\(\omega\) 基本概念 \(\omega\)

  在初中阶段就有所接触：整式可以包含加、减、乘、除、乘方五种对变量的运算，同时要求除数不含有变量。设 \(x,y\) 为变量，其余字母为常量，则 \(xy,a+by\) 是整式，\(\sqrt{a}x+\pi y~(a\ge0)\) 也是整式，因为根号下的 \(a\) 是常量；\(\frac{x}y,\sqrt{xy}\) 则不是整式。

  在本文中，我们所说的多项式通常指一元多项式，即仅含一个变量 \(x\) 的多项式。并简记一个多项式 \(A(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n\)，其中 \(n\) 是 \(A(x)\) 的次数。

\(\omega\) 系数表示法 & 点值表示法 \(\omega\)

  在上文中 \(A(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n\) 就是多项式的系数表示法。而可以证明，对于一个 \(n\) 次多项式，可以用任意 \(n+1\) 个其函数图像上不重合的点来唯一确定这个多项式。我们任取 \(n+1\) 个横坐标的值 \(x_0,x_1,\dots,x_n\)，代入 \(A(x)\)，求得 \(n+1\) 个点 \((x_0,y_0),(x_1,y_1),\dots,(x_n,y_n)\)，就可以用这 \(n+1\) 个点唯一确定 \(A(x)\)，这也被称为 \(A(x)\) 的点值表示法。注意到 \(x\) 是任意的，所以同一个多项式的点值表示法不唯一。

  接下来，抛出我们的问题：设有两个多项式 \(A(x),B(x)\)，如何计算它们的乘积（亦称作卷积） \(C(x)=A(x)\cdot B(x)\) 呢？

  一个简单的想法，我们可以利用乘法分配律求到 \(C(x)\) 每一项的系数。于是：

\[C(x)=\sum_{i=0}^{+\infty}\left(\sum_{j+k=i}a_jb_k\right)x^i \]

  注意求和中的 \(+\infty\) 只是一种形式记法，事实上，当 \(i\) 大于 \(A(x)\) 的次数与 \(B(x)\) 的次数之和时，\(x^i\) 的系数 \(c_i\) 显然为 \(0\)。

  不过呢……从算法设计的角度，这种求多项式乘法的方式的复杂度是 \(\mathcal{O}(n^2)\) 的，好慢 qwq。

  联系到点值表示法，如果对于同一个横坐标 \(x\)，其在 \(A(x)\) 上的坐标为 \((x,y_a)\)，在 \(B(x)\) 上的坐标为 \((x,y_b)\)，那么代入最初的表达式，它在 \(C(x)=A(x)\cdot B(x)\) 上的坐标就是 \((x,y_ay_b)\) 呐。所以，在已知 \(A(x)\) 和 \(B(x)\) 的点值表示法时，我们可以用 \(\mathcal{O}(n)\) 的时间求出 \(C(x)\) 的点值表示法！

\(\omega\) 傅里叶（Fourier）变换 \(\omega\)

  我们继续解决上文多项式乘法的问题——找到一个高效的算法，实现系数与点值表示法的转换。

  本节中，若非特别说明，\(n=2^k,k\in\mathbb{N}\)。

\(\omega\) 概述 \(\omega\)

  离散傅里叶变换（Discrete Fourier Transform，DFT），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其 DTFT 的频域采样。

  FFT 是一种高效实现 DFT 的算法，称为快速傅立叶变换（Fast Fourier Transform，FFT）。它对傅里叶变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。

\(\omega\) 前置知识 - 复数 \(\omega\)

  其实很简单：我们把形如 \(z=a+bi\) 的数称为复数，其中 \(a,b\in\mathbb R\)； \(a\) 为实部，\(b\) 为虚部，\(i\) 有 \(i^2=-1\)，为虚数单位。我们可以把复数与二维平面上的向量 \((a,b)\) 一一对应，此时 \(x\) 轴称为实轴，\(y\) 轴称为虚轴。并记其与 \(x\) 轴正方向的夹角为辐角 \(\theta\)，向量的模长为 \(|z|\)。如图，对于 \(z=3+2i\)：

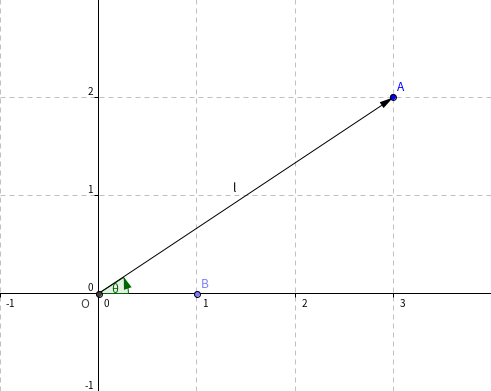
  其中 \(l\) 为模长，\(\theta\) 为辐角。接下来我们研究复数的一些基本运算：

• 加减法：\(z_1\pm z_2=(a_1\pm a_2)+(b_1\pm b_2)i\)。

• 乘法：\(z_1z_2=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i\)。

    进一步研究，发现：

  \[|z_1z_2|^2=(a_1^2a_2^2-2a_1a_2b_1b_2+b_1^2b_2^2)+(a_1^2b_2^2+2a_1a_2b_1b_2+a_2^2b_1^2)=(a_1^2+b_1^2)(a_2^2+b_2^2) \]

    最后一步用了简单的因式分解技巧。由于 \(a_1^2+b_1^2=|z_1|^2,a_2^2+b_2^2=|z_2|^2\)，所以有 \(|z_1z_2|=|z_1||z_2|\)。

    此外，运用 \(\tan\) 的和角公式，还可以求到 \(\theta_{z_1z_2}=\theta_{z_1}+\theta_{z_2}\)。

    所以，复数的乘法有一个重要的几何意义：模长相乘，辐角相加。

    最后，我们定义 \(\overline{z}\) 为 \(z\) 关于 \(x\) 轴对称的向量，称为 \(z\) 的共轭复数。即若 \(z=a+bi\)，有 \(\overline{z}=a-bi\)。可以发现 \(z\cdot\overline{z}=a^2+b^2\in\mathbb R\)。 为后文方便叙述，记 \(\operatorname{conj}(z)=\overline z\)。

\(\omega\) 单位根 \(\omega\)

  定义 \(n\) 次单位根为所有满足 \(z^n=1\) 的 \(z\)。根据乘法的几何意义，可知 \(|z|=1\)，\(n\theta_z=2k\pi\)，其中 \(k\in\mathbb{Z}\)。于是满足条件且小于 \(2\pi\) 的 \(\theta_z\) 集合为 \(\{0,\frac{1\times2\pi}{n},\frac{2\times2\pi}{n},\dots,\frac{(n-1)\times2\pi}{n}\}\)，共 \(n\) 个。我们记 \(\omega_n^k\) （\(\omega\)，/'əʊmɪɡə/）为第 \(k\) 个 \(n\) 次单位根（\(k=0,1,\dots,n-1\)）。如图，当 \(n=8\) 时：

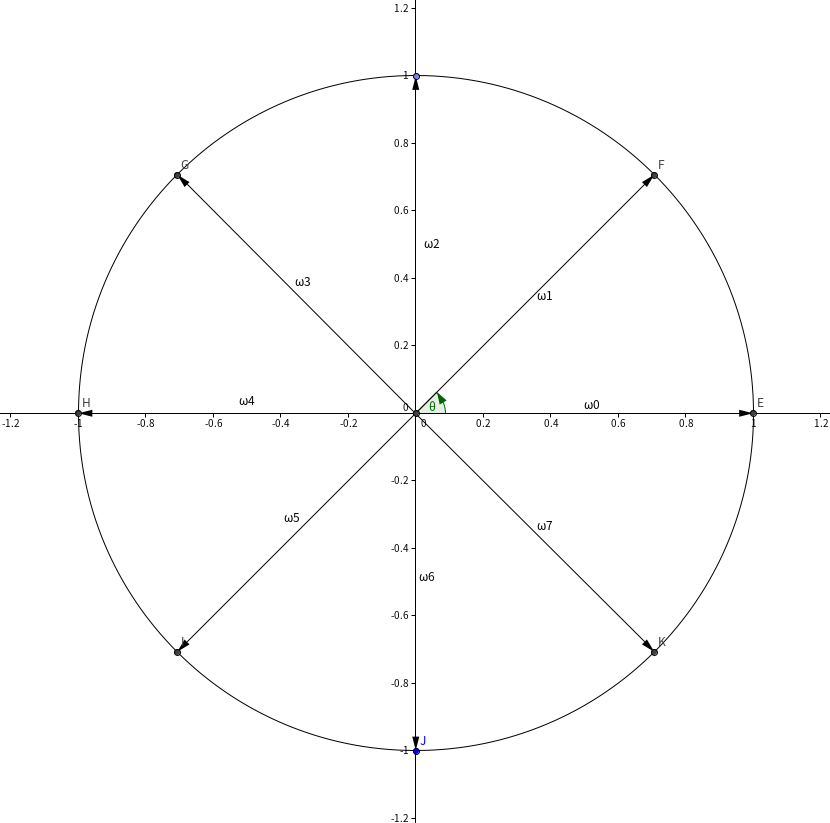
  运用简单的三角函数知识，得到：

\[\omega_n^k=(\cos\frac{2\pi k}{n},\sin\frac{2\pi k}{n}) \]

  可以发现，单位根实际上体现了一个周期意义：\(\omega_n^n=\omega_n^0\)。所以此后单位根的上标（乘方或是编号，它们在运算意义上等价）默认对单位根次数取模。单位根有如下性质：

• \(\omega_n^j\omega_n^k=\omega_n^{j+k}\)。
• \(\omega_{kn}^{kj}=\omega_n^j\)。
• \(\omega_{2n}^k=-\omega_{2n}^{k+n}\)。

  可以结合乘法几何意义与公式理解。

\(\omega\) 快速傅里叶正变换（FFT）\(\omega\)

  有必要重申我们的目标：实现系数与点值表示法的转换。

  现在，设有 \(A(x)=a_0+a_1x+a_2x^2+\cdots+a_{n-1}x^{n-1}\)，我们希望代入 \(n\) 次单位根 \(\omega_n^0,\omega_n^1,\dots,\omega_n^{n-1}\) 这 \(n\) 个复数来取得 \(A(x)\) 的点值表示法。

  分开奇数项与偶数项，记：

\[A_e(x)=\sum_{i\in[0,n)\land2|i}a_ix^{\frac{i}2} \]

\[A_o(x)=\sum_{i\in[0,n)\land2\not|i}a_ix^{\frac{i-1}2} \]

  利用 \(A_e(x)\) 和 \(A_o(x)\) 来表示 \(A(x)\)，有：

\[A(x)=A_e(x^2)+xA_o(x^2) \]

  设 \(n=2m\)，尝试代入一个 \(\omega_n^k\)：

\[A(\omega_n^k)=A_e(\omega_n^{2k})+\omega_n^kA_o(\omega_n^{2k}) \]

  注意到 \(\omega_n^{2k}=\omega_{2m}^{2k}=\omega_m^k\)，所以：

\[A(\omega_n^k)=A_e(\omega_m^k)+\omega_n^kA_o(\omega_m^k) \]

  类似地，代入 \(\omega_n^{k+m}=-\omega_n^k\)，有：

\[A(\omega_n^{k+m})=A_e(\omega_m^k)-\omega_n^kA_o(\omega_m^k) \]

  所以，当已知 \(A_e(\omega_m^k)\) 和 \(A_o(\omega_m^k)\) 时，可以 \(\mathcal{O}(1)\) 计算出 \(A(\omega_n^k)\) 和 \(A(\omega_n^{k+m})\)。现在，就有了一个算法雏形：

Function name: FFT.

Input: a polynomial \(A(x)=a_0+a_1x_1+\cdots\) which's length is \(n~(n=2^k,k\in\mathbb N)\).

Output: a set \(\mathcal A=\{A(\omega_n^0),A(\omega_n^1),\dots,A(\omega_n^{n-1})\}\).

if \(n=1\) then

 return \(\{(a_0,0)\}\)

\(m\leftarrow\frac{n}2\)

\(A_e(x)\leftarrow\sum_{i\in[0,n)\land2|i}a_ix^{\frac{i}2}\)

\(A_o(x)\leftarrow\sum_{i\in[0,n)\land2\not|i}a_ix^{\frac{i-1}2}\)

\(\mathcal A\leftarrow\varnothing\)

\(\mathcal{A}_e\leftarrow\operatorname{FFT}(A_e,m)\)

\(\mathcal{A}_o\leftarrow\operatorname{FFT}(A_o,m)\)

\(k\leftarrow0\)

while \(k<m\) do

 \(\mathcal{A}_k\leftarrow{\mathcal{A}_e}_k+\omega_n^k{\mathcal{A}_o}_k\)

​ \(\mathcal{A}_{k+m}\leftarrow{\mathcal{A}_e}_k-\omega_n^k{\mathcal{A}_o}_k\)

​ \(k\leftarrow k+1\)

return \(\mathcal A\)

  复杂度是 \(\mathcal{T}(n)=2\mathcal{T}(\frac{n}2)+\mathcal{O}(n)=\mathcal{O}(n\log n)\)。在后文中，“多项式 \(A(x)\) 的点值表示”均指由上述 FFT 算法得到的 \(\mathcal A\)。

  别着急做题，这种实现方法 SPFA 了 qwq。

\(\omega\) 快速傅里叶逆变换（IFFT）\(\omega\)

  利用 FFT，我们可以快速地将系数表示法转换成点值表示法，那怎么在同样优秀的复杂度内转回去呢？

  从本质入手，考虑到 \(\mathcal A_j=\sum_{k=0}^{n-1}a_k(\omega_n^j)^k\)，我们把它写成矩阵乘法的形式：

\[\begin{bmatrix} (\omega_n^0)^0&(\omega_n^0)^1&\cdots&(\omega_n^0)^{n-1}\\ (\omega_n^1)^0&(\omega_n^1)^0&\cdots&(\omega_n^1)^{n-1}\\ \vdots&\vdots&\ddots&\vdots\\ (\omega_n^{n-1})^0&(\omega_n^{n-1})^1&\cdots&(\omega_n^{n-1})^{n-1} \end{bmatrix} \begin{bmatrix} a_0\\a_1\\\vdots\\a_{n-1} \end{bmatrix}= \begin{bmatrix} \mathcal A_0\\ \mathcal A_1\\ \vdots\\ \mathcal A_{n-1} \end{bmatrix} \]

  令左侧的系数矩阵为 \(U\)，考虑系数矩阵 \(V\)：

\[V=\begin{bmatrix} (\omega_n^{-0})^0&(\omega_n^{-0})^1&\cdots&(\omega_n^{-0})^{n-1}\\ (\omega_n^{-1})^0&(\omega_n^{-1})^0&\cdots&(\omega_n^{-1})^{n-1}\\ \vdots&\vdots&\ddots&\vdots\\ (\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\cdots&(\omega_n^{-(n-1)})^{n-1} \end{bmatrix} \]

  那么：

\[(U\cdot V)_{ij}=\sum_{k=0}^{n-1}u_{ik}v_{kj}=\sum_{k=0}^{n-1}\omega_n^{k(j-i)} \]

  当 \(i=j\) 时，显然 \((U\cdot V)_{ij}=n\)。

  当 \(i\not=j\) 时，发现是等比数列的形式。所以 \((U\cdot V)_{ij}=\frac{1-\omega_n^{n(j-i)}}{1-\omega_n^{j-i}}\)。又因为 \(\omega_n^n=\omega_n^0=1\)，所以分子有 \(1-1=0\)，则原式 \(=0\)。

  综上，\((U\cdot V)_{ij}=[i=j]n\)，即 \(\frac{1}nV=U^{-1}\)。

  以此，就有：

\[\begin{bmatrix} a_0\\a_1\\\vdots\\a_{n-1} \end{bmatrix}=\frac{1}{n}V\begin{bmatrix} \mathcal A_0\\ \mathcal A_1\\ \vdots\\ \mathcal A_{n-1} \end{bmatrix}= \frac{1}n\begin{bmatrix} (\omega_n^{-0})^0&(\omega_n^{-0})^1&\cdots&(\omega_n^{-0})^{n-1}\\ (\omega_n^{-1})^0&(\omega_n^{-1})^0&\cdots&(\omega_n^{-1})^{n-1}\\ \vdots&\vdots&\ddots&\vdots\\ (\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\cdots&(\omega_n^{-(n-1)})^{n-1} \end{bmatrix} \begin{bmatrix} \mathcal A_0\\ \mathcal A_1\\ \vdots\\ \mathcal A_{n-1} \end{bmatrix} \]

  注意到 \(\omega_n^{-k}=\omega_n^{n-k}\)，所以依然能够用 FFT 的递归形式求解。

\(\omega\) 迭代实现 \(\omega\)

  常数惊人呐……

  这里，我们将尝试把递归的 FFT Fast-Fast TLE 转换为仅用循环迭代的 FFT。

  观察递归时各系数的位置：

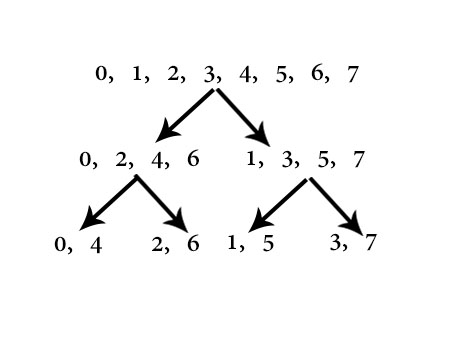
  观察第一层和最后一层：

原序列 dec	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)
原序列 bin	\(000\)	\(001\)	\(010\)	\(011\)	\(100\)	\(101\)	\(110\)	\(111\)
新序列 dec	\(0\)	\(4\)	\(2\)	\(6\)	\(1\)	\(5\)	\(3\)	\(7\)
新序列 bin	\(000\)	\(100\)	\(010\)	\(110\)	\(001\)	\(101\)	\(011\)	\(111\)

  发现原序列下标的二进制翻转过来就是新序列下标。

  所以我们可以先安排好新序列下标，再从下往上迭代就可以了。

\(\omega\) 例题 \(\omega\)

\(\omega\)「洛谷 P3803」「模板」多项式乘法（FFT）\(\omega\)

\(\omega\) 题意简述 \(\omega\)

  link.

  给两个多项式的每项系数，求其相乘得到的多项式的每项系数。

\(\omega\) 数据规模 \(\omega\)

  多项式长度 \(n,m\le10^6\)。

\(\omega\) \(\text{Solution}\) \(\omega\)

  直接给出完整代码，建议先模仿实现，以免常数惊人 owo。

  不过我不知道怎么折叠显示代码，影响阅读很抱歉 qwq。

\(\omega\) \(\text{Code}\) \(\omega\)

#include <cmath>
#include <cstdio>
#include <iostream>

inline int rint () {
	int x = 0, f = 1; char s = getchar ();
	for ( ; s < '0' || '9' < s; s = getchar () ) f = s == '-' ? -f : f;
	for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
	return x * f;
}

template<typename Tp>
inline void wint ( Tp x ) {
	if ( x < 0 ) putchar ( '-' ), x = -x;
	if ( 9 < x ) wint ( x / 10 );
	putchar ( x % 10 ^ '0' );
}

const int MAXL = 1 << 21;
const double PI = acos ( -1 );
int n, m, rev[MAXL + 5];

struct Complex { // 复数结构体。
	double x, y;
	Complex () {} Complex ( const double tx, const double ty ): x ( tx ), y ( ty ) {}
	inline Complex operator + ( const Complex t ) const { return Complex ( x + t.x, y + t.y ); }
	inline Complex operator - ( const Complex t ) const { return Complex ( x - t.x, y - t.y ); }
	inline Complex operator * ( const Complex t ) const { return Complex ( x * t.x - y * t.y, x * t.y + y * t.x ); }
	inline Complex operator / ( const double t ) const { return Complex ( x / t, y / t ); }
} A[MAXL + 5], B[MAXL + 5];

inline void FFT ( const int n, Complex* A, const int tp ) {
	// n为多项式长度，保证是2的整数幂；A为每项系数；tp=1表示正变换，tp=-1表示逆变换。
	for ( int i = 0; i < n; ++ i ) if ( i < rev[i] ) std :: swap ( A[i], A[rev[i]] ); // 安排系数位置。
	for ( int i = 2, stp = 1; i <= n; i <<= 1, stp <<= 1 ) {
		Complex w ( cos ( PI / stp ), tp * sin ( PI / stp ) ); // 当前正在处理$\omega_i$。
		for ( int j = 0; j < n; j += i ) {
			Complex r ( 1, 0 );
			for ( int k = 0; k < stp; ++ k, r = r * w ) {
				// $r=\omega_i^k$。
				Complex ev ( A[j + k] ), ov ( r * A[j + k + stp] );
				A[j + k] = ev + ov, A[j + k + stp] = ev - ov;
			}
		}
	}
	if ( ! ~ tp ) for ( int i = 0; i < n; ++ i ) A[i] = A[i] / n; // 逆变换，最后每项/n。
}

inline void ployConv ( const int n, const int m, const Complex* A, const Complex* B, Complex* C ) {
	// 计算A(x)与B(x)的卷积，答案为C(x)。
	int lg = 0, len = 1;
	static Complex tmpA[MAXL + 5], tmpB[MAXL + 5];
	for ( ; len < n + m - 1; len <<= 1, ++ lg ); // C(x)长度为n+m-1，找到适合的长度len。
	for ( int i = 0; i < len; ++ i ) {
		tmpA[i] = A[i], tmpB[i] = B[i];
		rev[i] = ( rev[i >> 1] >> 1 ) | ( ( i & 1 ) << lg >> 1 ); // rev[i]为i翻转后的位置，自行理解。
	}
	FFT ( len, tmpA, 1 ), FFT ( len, tmpB, 1 ); // 正变换求到点值表示。
	for ( int i = 0; i < len; ++ i ) C[i] = tmpA[i] * tmpB[i]; // 求到C(x)的点值表示。
	FFT ( len, C, -1 ); // 逆变换求到C(x)。
}

int main () {
	n = rint () + 1, m = rint () + 1; // 注意这里要+1。
	for ( int i = 0; i < n; ++ i ) A[i].x = rint ();
	for ( int i = 0; i < m; ++ i ) B[i].x = rint ();
	ployConv ( n, m, A, B, A );
	for ( int i = 0; i < n + m - 1; ++ i ) {
		wint ( ( int ) round ( A[i].x ) );
		putchar ( i == n + m - 2 ? '\n' : ' ' );
	}
	return 0;
}

\(\omega\) 快速数论变换（NTT）\(\omega\)

  事实上，由于 FFT 存在大量浮点数运算，其精度和常数都不尽人意。那么能否在整数域下找到单位根的替代品呢？

  我们来总结一下单位根应具有的性质：

• \(\omega_n^j\omega_n^k=\omega_n^{j+k}\)，注意这里的上标就意义上来说不是乘方，而是编号（当然运算上就是乘方 www）。
• \(\omega_{kn}^{kj}=\omega_n^j\)，我们需要这个性质进行递归处理。
• \(\omega_{2n}^k=-\omega_{2n}^{k+n}\)，这一性质体现在了合并计算的步骤。
• \((\forall j\not=k)(\omega_n^j\not=\omega_n^k)\)，它保证了点值表示法的坐标不重合。
• \(\omega_n^0=1\)，它保证了逆变换顺利进行。

  考虑在模意义下……

\(\omega\) 原根 \(\omega\)

  OI-Wiki 讲得好高深 qwq……

  对于素数 \(p\)，定义其原根 \(g\) 为满足 \((\forall j,k\in[0,p-1),j\not=k)\left(g^j\not\equiv g^k\pmod p\right)\) 的数。模仿 \(\omega\) 的定义，我们令 \(\alpha_n^k=(g^\frac{p-1}n)^k\)（这里 \(\alpha\) 是随便取的名字 www），考虑其是否满足上述几条性质：

• \(\alpha_n^j\alpha_n^k\equiv\alpha_n^{jk}\pmod p\)，乘方性质，显然。
• \(\alpha_{kn}^{kj}=(g^\frac{p-1}{kn})^{kj}=(g^\frac{p-1}n)^j=\alpha_n^j\)，成立。
• \(-\alpha_{2n}^{k+n}=-g^\frac{(p-1)(k+n)}{2n}=(-g^\frac{p-1}2)g^\frac{(p-1)k}{2n}\equiv g^\frac{(p-1)k}{2n}=\alpha_{2n}^k\pmod p\)。注意因为 \((g^\frac{p-1}{2})^2\equiv1\pmod p\) 且根据 \(g\) 的定义， \(g^\frac{p-1}2=\alpha_{2n}^n\not=\alpha_{2n}^0\land\alpha_{2n}^0\equiv1\pmod p\)，所以 \(g^\frac{p-1}2\equiv-1\pmod p\)，等式成立。
• 由定义，成立。
• 显然 \(g\not=0\)，成立。

  于是，把 FFT 中的所有 \(\omega_n^k\) 替换为 \(\alpha_n^k\) 就变成 NTT 啦！记得取模 owo。

\(\omega\) 实现 \(\omega\)

inline void NTT ( const int n, int* A, const int tp ) {
	for ( int i = 0; i < n; ++ i ) if ( i < rev[i] ) A[i] ^= A[rev[i]] ^= A[i] ^= A[rev[i]];
	for ( int i = 2, stp = 1, w; i <= n; i <<= 1, stp <<= 1 ) {
		w = qkpow ( G, ( MOD - 1 ) / i );
              // G为原根，qkpow(a,b)为a的b次方模MOD的结果。
		if ( ! ~ tp ) w = qkpow ( w, MOD - 2 );
		for ( int j = 0; j < n; j += i ) {
			for ( int r = 1, k = j; k < j + stp; ++ k, r = 1ll * r * w % MOD ) {
				int ev = A[k], ov = 1ll * r * A[k + stp] % MOD;
				A[k] = ( ev + ov ) % MOD, A[k + stp] = ( ev - ov + MOD ) % MOD;
			}
		}
	}
	if ( ! ~ tp ) {
		int invn = qkpow ( n, MOD - 2 ); // invn为n的逆元。
		for ( int i = 0; i < n; ++ i ) A[i] = 1ll * A[i] * invn % MOD;
	}
}

\(\omega\) NTT 模数 \(\omega\)

  注意到，\(n\) 的大小是随多项式长度变化的，而我们必须保证 \(n|(p-1)\)，所以 \(p-1\) 所含 \(2\) 的因子个数决定了 NTT 能够接受的最大多项式长度。对于素数 \(p\) 的选取自然也有了考究。

  记住一点，\(998244353-1=2^{23}\times119\)，适合做 NTT 模数，原根为 \(3\)；\(10^9+7-1=2\times500000003\)，不适合做 NTT 模数。

  更多 NTT 模数可见这篇博客。

  到此，多项式最最基础的知识就结束啦。

\(\omega\) 奇怪的模数 - 任意模数 NTT \(\omega\)

  你 NTT 对模数有要求对吧？出题人就笑了……/xyx

  好吧，在不接受 FFT 精度误差的情况下，我们来想想办法应对模数不是 NTT 模数，甚至不是素数的毒瘤题吧！

\(\omega\) 三模 NTT \(\omega\)

  我偏要用 NTT 模数 www。

  顾名思义，我们任取三个 NTT 模数 \(p_1,p_2,p_3\)，分别求出多项式乘积的第 \(k\) 项模 \(p_1,p_2,p_3\) 的结果，然后用中国剩余定理（CRT）解出该项模题目给定模数 \(M\) 的结果就行了。不熟悉 CRT 的读者可以参考这篇博客。

  我个人认为不太优美懒，因此没有具体实现。在抱歉之余推荐这篇博客的模板 owo。

\(\omega\) 拆系数 FFT（MTT）\(\omega\)

  我偏要用 FFT。

  缩写释义：MTT - MaoXiao Theory(?) Transformation。快速毛论变换（雾。

  假设多项式 \(A(x)=a_0+a_1x+a_2x^2+\cdots,B(x)=b_0+b_1x+b_2x^2+\cdots\)，长度均为 \(n\)，给定的模数 \(m\)，我们要求它们的卷积 \(R(x)=A(x)\cdot B(x)\)。如果直接 FFT，最大的系数可达到 \(nm^2\) 的级别。我们假定 \(n\le10^5,m\le10^9\)，那么这样的精度误差是不被接受的。我们取 \(M=\lceil\sqrt m\rceil\)，并定义以下几个多项式：

\[\begin{aligned} C(x)&=\sum_{k=0}^{n-1}(a_k\bmod M)x^k\\ D(x)&=\sum_{k=0}^{n-1}\frac{a_k-(a_k\bmod M)}{M}x^k\\ E(x)&=\sum_{k=0}^{n-1}(b_k\bmod M)x^k\\ F(x)&=\sum_{k=0}^{n-1}\frac{a_k-(a_k\bmod M)}{M}x^k \end{aligned} \]

  可以发现，以上每个多项式的系数都是不超过 \(M\) 的，那么任意两个多项式卷积的最大系数不超过 \(nM^2\le10^{14}\)，在 double 的承受范围以内。（保险起见，建议开 long double，不过对于某些 g++ 版本貌似并没有作用 owo。）我们用这四个多项式表示 \(R(x)\)：

\[R(x)=M^2\cdot D(x)F(x)+M\cdot\left(C(x)F(x)+D(x)E(x)\right)+C(x)E(x) \]

  这样，在 FFT 过程中，系数大小能被接受；作系数拼凑时步步取模亦能保证不溢出，我们就用 FFT 解决了任意模数 NTT 的问题。一般来说，取 \(M=32768=2^{15}\)，可以用位运算节省常数；还应利用 \(\omega_n^k\) 的通项预处理出所有单位根以保障精度。

\(\omega\) 七次转五次 \(\omega\)

  数一数，我们对 \(C(x),D(x),E(x),F(x)\) 分别进行了一次 FFT，对 \(D(x)F(x),\) \(C(x)F(x)+D(x)E(x),\) \(C(x)E(x)\) 分别进行了一次 IFFT，一共有七次变换操作，常数有点点大 qwq。

  接下来，我们假设有实系数多项式 \(A(x)=a_0+a_1x+a_2x^2+\cdots,B(x)=b_0+b_1x+b_2x^2+\cdots\)，长度均为 \(n~(n=2^k,k\in\mathbb N)\)，我们希望分别求到它们的点值表示 \(\mathcal A\) 和 \(\mathcal B\)。于是定义：

\[P(x)=A(x)+iB(x) \]

\[Q(x)=A(x)-iB(x) \]

  其中 \(i\) 是虚数单位。设 \(P\) 与 \(Q\) 的点值表示分别为 \(\mathcal P,\mathcal Q\)，并记 \(\omega_n^k\) 的辐角 \(\frac{2\pi k}n\) 为 \(\theta_n^k\)。那么：

\[\begin{aligned} \mathcal P_k&=A(\omega_n^k)+iB(\omega_n^k)\\ &=\sum_{j=0}^{n-1}a_j\omega_n^k+ib_j\omega_n^k\\ &=\sum_{j=0}^{n-1}(a_j+ib_j)(\cos\theta_n^k+i\sin\theta_n^k)\\\\ \mathcal Q_k&=A(\omega_n^k)-iB(\omega_n^k)\\ &=\sum_{j=0}^{n-1}a_j\omega_n^{jk}-ib_j\omega_n^{jk}\\ &=\sum_{j=0}^{n-1}(a_j-ib_j)(\cos\theta_n^{jk}+i\sin\theta_n^{jk})\\ &=\sum_{j=0}^{n-1}(a_j\cos\theta_n^{jk}+b_j\sin\theta_n^{jk})+i(a_j\sin\theta_n^{jk}-b_j\cos\theta_n^{jk})\\ &=\operatorname{conj}\left(\sum_{j=0}^{n-1}(a_j\cos\theta_n^{jk}+b_j\sin\theta_n^{jk})-i(a_j\sin\theta_n^{jk}-b_j\cos\theta_n^{jk})\right)\\ &=\operatorname{conj}\left(\sum_{j=0}^{n-1}\left(a_j\cos(-\theta_n^{jk})-b_j\sin(-\theta_n^{jk})\right)+i\left(a_j\sin(-\theta_n^{jk})-b_j\cos(-\theta_n^{jk})\right)\right)\\ &=\operatorname{conj}\left(\sum_{j=0}^{n-1}(a_j+ib_j)\left(\cos(-\theta_n^{jk})+i\sin(-\theta_n^{jk})\right)\right)\\ &=\operatorname{conj}\left(\sum_{j=0}^{n-1}(a_j+ib_j)\left(\cos\theta_n^{-jk}+i\sin\theta_n^{-jk}\right)\right)\\ &=\operatorname{conj}\left(\sum_{j=0}^{n-1}(a_j+ib_j)\left(\cos\theta_n^{(n-k)j}+i\sin\theta_n^{(n-k)j}\right)\right)\\ &=\operatorname{conj}(\mathcal P_{n-k}) \end{aligned} \]

  推导时，时刻留意 \(\theta_n\) 的上标在模 \(n\) 意义下嗷！

  最终，发现 \(\mathcal Q\) 可以在求得 \(\mathcal P\) 的前提下 \(\mathcal O(1)\) 求到。只需要用 \(\mathcal P\) 和 \(\mathcal Q\) 表示出 \(\mathcal A\) 和 \(\mathcal B\)：

\[\mathcal A_k=\frac{\mathcal P_k+\mathcal Q_k}2\\ \mathcal B_k=i\frac{\mathcal Q_k-\mathcal P_k}2 \]

  就可以用一次 FFT 求出两个多项式的点值表示啦！（我认为毛啸的论文在 \(\mathcal B_k\) 的表达式处有误，右侧分子应为本文的 \(\mathcal Q_k-\mathcal P_k\) 而非 \(\mathcal P_k-\mathcal Q_k\)，欢迎指正 qwq。）

  于是，我们可以把对 \(C(x),D(x),E(x),F(x)\) 的 FFT 合并为两组，就只需要五次 FFT 啦！

\(\omega\) 五次转四次 \(\omega\)

  正变换已经足够优秀了，我们接下来考虑逆变换的合并。按照上文的推导，我们只需要求到 \(P(x)\) 或者 \(Q(x)\) 就可以了——因为原多项式是实系数的，所以对于 \(P(x)\) 或 \(Q(x)\) 的每一项，我们能够区分出其实部就是 \(A(x)\) 的系数而虚部就是 \(B(x)\) 的系数。既然已知 \(\mathcal A\) 和 \(\mathcal B\)，直接利用定义式，有：

\[\mathcal P_k=\mathcal A_k+i\mathcal B_k \]

  逆变换 \(\mathcal P\) 得到 \(P(x)\)，就可以把两次逆变换合并为一次了。最终，我们把四次正变换合并为两次，三次逆变换合并为两次，仅用四次 FFT 就解决了这一问题。

\(\omega\) 例题 \(\omega\)

\(\omega\) 「洛谷 P4245」「模板」任意模数 NTT

\(\omega\) 题意简述 \(\omega\)

  link.

  给两个多项式，求其在模 \(p\) 意义下的卷积。

\(\omega\) 数据规模 \(\omega\)

  多项式长度 \(n\le10^5\)，系数 \(a_k,b_k\le10^9\)，\(p\le10^9+9\)。

\(\omega\) \(\text{Solution}\) \(\omega\)

  这里仅给出四次 FFT 的 MTT 做法。

\(\omega\) \(\text{Code}\) \(\omega\)

#include <cmath>
#include <cstdio>
#include <iostream>

typedef long long LL;

inline int rint () { /* 快读 */ }

inline void wint ( const int x ) { /* 快输 */ }

const int MAXN = 1 << 18;
const double PI = acos ( -1 );
int n, m, p, A[MAXN + 5], B[MAXN + 5], rev[MAXN + 5];

struct Complex {
	/* 复数结构体 */
} omega[MAXN + 5], P[MAXN + 5], Q[MAXN + 5], C[MAXN + 5], D[MAXN + 5], E[MAXN + 5], F[MAXN + 5];

inline void FFT ( const int n, Complex* A, const int tp ) { /* FFT，应使用预处理好的单位根omega[]。 */ }

int main () {
	n = rint () + 1, m = rint () + 1, p = rint ();
	for ( int i = 0; i < n; ++ i ) A[i] = rint () % p, P[i] = Complex ( A[i] & 0x7fff, A[i] >> 15 );
	for ( int i = 0; i < m; ++ i ) B[i] = rint () % p, Q[i] = Complex ( B[i] & 0x7fff, B[i] >> 15 );
	int lg = 0, len = 1;
	for ( ; len < n + m - 1; len <<= 1, ++ lg );
	for ( int i = 0; i < len; ++ i ) rev[i] = ( rev[i >> 1] >> 1 ) | ( ( i & 1 ) << lg >> 1 );
	for ( int i = 1; i < len; i <<= 1 ) { // 预处理单位根。
		for ( int k = 0; k < i; ++ k ) {
			omega[len / i * k] = Complex ( cos ( PI * k / i ), sin ( PI * k / i ) );
		}
	}
	FFT ( len, P, 1 ), FFT ( len, Q, 1 );
	for ( int i = 0; i < len; ++ i ) {
		Complex t ( P[( len - i ) % len].x, -P[( len - i ) % len].y );
		C[i] = ( P[i] + t ) / 2, D[i] = Complex ( 0, 1 ) * ( t - P[i] ) / 2;
	}
	for ( int i = 0; i < len; ++ i ) {
		Complex t ( Q[( len - i ) % len].x, -Q[( len - i ) % len].y );
		E[i] = ( Q[i] + t ) / 2, F[i] = Complex ( 0, 1 ) * ( t - Q[i] ) / 2;
	}
	for ( int i = 0; i < len; ++ i ) {
		Complex c ( C[i] ), d ( D[i] ), e ( E[i] ), f ( F[i] );
		C[i] = c * e, D[i] = c * f + d * e, E[i] = d * f;
		P[i] = C[i] + Complex ( 0, 1 ) * E[i];
	}
	FFT ( len, D, -1 ), FFT ( len, P, -1 );
	for ( int i = 0; i < n + m - 1; ++ i ) {
		int c = ( LL ( P[i].x + 0.5 ) % p + p ) % p, d = ( LL ( D[i].x + 0.5 ) % p + p ) % p, e = ( LL ( P[i].y + 0.5 ) % p + p ) % p;
		wint ( ( c + ( 1ll << 15 ) % p * d % p + ( 1ll << 30 ) % p * e % p ) % p );
		putchar ( i + 1 == n + m - 1 ? '\n' : ' ' );
	}
	return 0;
}

\(\omega\) 「CF 623E」Transforming Sequence \(\omega\)

\(\omega\) 题意简述 \(\omega\)

  link.

  求有多少个长度为 \(n\) 的序列 \(\{a_n\}\)，满足 \(a_k\in(0,2^k)\land a_k\not\subseteq\bigcup_{j=1}^{k-1}a_j\)。这里的集合运算把 \(a_k\) 作为了二进制集合。对 \(10^9+7\) 取模。

\(\omega\) 数据规模 \(\omega\)

  \(n\le10^{18},k\in[1,3\times10^4]\)。

\(\omega\) \(\text{Solution}\) \(\omega\)

  详见我的题解。题意描述略有不同，请自行理解。为什么我的 MTT 有八次变换啊……

  专门提起这道题的目的，除了让大家实战运用 MTT 之外，还想让大家感受倍增这种几乎能融入所有 OI 知识点的思想。

  本来还有多项式全家桶，但因为太懒所以烂尾咯 qwq。

\(\omega\) 参考资料 \(\omega\)

  按在文中第一次借鉴或引用的位置顺序排列：

• 多项式 @百度百科.
• 整式 @百度百科.
• 快速傅里叶变换 @OI-Wiki.
• 多项式乘法 @Tiw_Air_OAO.
• FFT 用到的各种素数 @Miskcoo's Space.
• 中国剩余定理 CRT @yyb.
• 再探快速傅里叶变换 @毛啸.（网上资源）