Solution -「NOI.AC 省选膜你赛」寄蒜几盒
题目
题意简述
给定一个含有 个顶点的凸多边形( 是偶数),对于每一对相对的边(即中间有 条其它边),延长它们以将平面分割为多块,并把包含原凸包的一块染色(包含边界)。再给出 个询问,询问一个点 所在位置是否被染色。
数据规模
强制在线,。
题解
题意转化
首先,考虑某个点“被染色”的条件:存在一对相对边,若两边不平行,则该点在这对边延长所构成的劣角内部;若两边平行,则该点在它们所在两条直线的异侧。下图表现了第一种情况: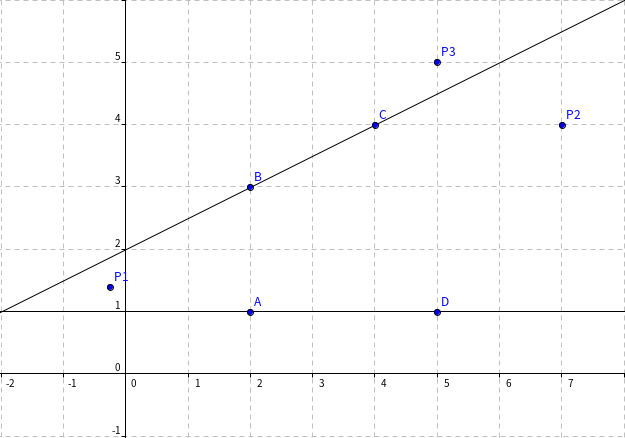
在图中,如果我们把凸多边形(四边形 )看作障碍物,那么 看不到 两边, 亦是如此,而二者都被相对边 染色了。相反,对于 ,它能看到 这条边,所以没有被这对边染色。
尝试把这个结论推广,对于任意一点 ,若存在 看不到的一对相对边, 就会被染色,反之则不会被染色。所以,对于不会被染色的 ,它至少能看到多边形 条边。
算法构建
第一步,我们要得到判断“一组相对边是否能染色某个点”的方法。还是以上图为例:
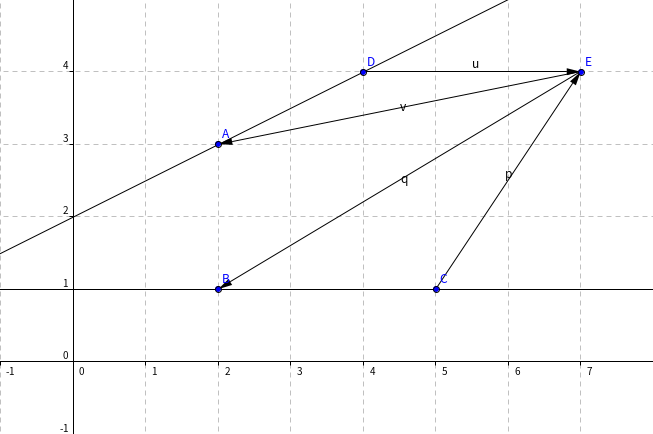
对于 点,我们求出向量 (注意在这里 四点是按逆时针排列的)。并记 ,可以发现,当 为真时, 被这组边染色。
第二步,还需要判断“一个点能否看到多边形上的某个点”。其实很简单,只需要令第一步中 重合, 分别为多边形上的前驱和后继顶点,如第一步判断能否染色就行啦~
第三步,如何求 能够看到几条边呢?不难想到二分:先取出一个会被看到的凸多边形上的点,再分别向两侧扩展。但怎么找到这个点呢?
找肯定是不可取的。我们耍一个小聪明:随便取一个点,设其在凸多边形上的下标为 ,并取出 这组对边,作第一步的判断。如果判断成功,就直接得出答案啦;否则, 就一定能看到这四个点中的两个(某一条边),再用第二步的方法就可以找到我们需要的点了。
最后,二分即可。
代码
#include <ctime>
#include <cstdio>
#include <cstdlib>
#include <utility>
typedef long long LL;
typedef __int128 LLL;
inline LL rint () {
LL x = 0, f = 1; char s = getchar ();
for ( ; s < '0' || '9' < s; s = getchar () ) f = s == '-' ? -f : f;
for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
return x * f;
}
const int MAXN = 1e5;
int T, N, Q;
struct Point { LLL x, y; } P[MAXN + 5];
struct Vector {
LLL x, y;
Vector () {}
Vector ( const Point p ): x ( p.x ), y ( p.y ) {}
Vector ( const LLL tx, const LLL ty ): x ( tx ), y ( ty ) {}
Vector ( const Point s, const Point t ): x ( t.x - s.x ), y ( t.y - s.y ) {}
inline LLL operator * ( const Vector t ) const { return x * t.y - y * t.x; }
};
inline bool visible ( const Point s, const int indx ) {
LLL t1 = Vector ( P[indx], s ) * Vector ( s, P[indx % N + 1] );
LLL t2 = Vector ( P[indx], s ) * Vector ( s, P[( indx - 2 + N ) % N + 1] );
bool ret = t1 > 0 || t2 < 0;
return ret;
}
int main () {
srand ( time ( 0 ) ^ 20120712 );
T = rint (), N = rint ();
for ( int i = 1; i <= N; ++ i ) P[i].x = rint (), P[i].y = rint ();
Q = rint ();
int cnt = 0;
for ( Point R; Q --; ) {
R.x = rint (), R.y = rint ();
if ( T ) R.x ^= 1ll * cnt * cnt * cnt, R.y ^= 1ll * cnt * cnt * cnt;
int p = rand () % N + 1, q = ( p + N / 2 - 1 ) % N + 1;
LLL t1 = Vector ( P[p], R ) * Vector ( R, P[p % N + 1] );
LLL t2 = Vector ( P[q % N + 1], R ) * Vector ( R, P[q] );
if ( ! t1 || ! t2 || ( t1 < 0 && t2 > 0 ) ) {
puts ( "DA" ), ++ cnt;
continue;
}
int rpos = visible ( R, p ) ? p : q;
int l = 0, r = N - 1, mid;
while ( l < r ) {
mid = l + r + 1 >> 1;
if ( visible ( R, ( rpos - mid - 1 + N ) % N + 1 ) ) l = mid;
else r = mid - 1;
}
int prelen = l;
l = 0, r = N - 1;
while ( l < r ) {
mid = l + r + 1 >> 1;
if ( visible ( R, ( rpos + mid - 1 ) % N + 1 ) ) l = mid;
else r = mid - 1;
}
int suflen = l;
if ( prelen + suflen >= N >> 1 ) puts ( "NE" );
else puts ( "DA" ), ++ cnt;
}
return 0;
}
分类:
A.算法/知识点 / 计算几何



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现