剑指offer刷题笔记(JAVA版)
剑指offer刷题笔记(JAVA版)
作者:光和影子
我的博客
前言
为了以后复习方便,在刷题的时候进行了记录。从第12题开始记录的,前面的题目等二刷再加进去吧,hhh
正在更新中。。。

T12. 矩阵中的路径
题目
难度:中等
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
[["a","b","c","e"],
["s","f","c","s"],
["a","d","e","e"]]
但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd"
输出:false
提示:
1 <= board.length <= 200
1 <= board[i].length <= 200
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/ju-zhen-zhong-de-lu-jing-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
展开查看
总体思路:本题中的二维表可以看作一个图,而给定的字符串就是图中指定的路径。因此要判断二维表中是否存在指定字符串的路径可以直接对图进行深度优先遍历(DFS)。
剪枝:为了优化性能,可以在搜索过程中一旦遇到不符合的路径立即停止此路径的搜索并返回,即可行性剪枝。
具体步骤:
- 从某一个结点开始进行遍历
- 若该节点的行列超出二维表board的界限则返回
false,表示此路径不通 - 若该节点不等于给定字符串对应的单词,则返回
false,表示此路径不通 - 将该节点置为一个不可能出现的值'\0'表示此结点在该路径下已经被访问过。即board[i][i]='\0'
- 对该节点的所有孩子结点进行步骤1-4,直到找到给定路径或没有孩子结点
- 若进行到此步说明该节点的所有孩子结点的所有路径都不能找到指定路径。此时进行回溯:将该结点的值还原,即board[i][i]=等于原来的值(即状态回滚),并返回。由于是递归过程,所以返回是返回到其父节点,且下一个即将要访问的是其兄弟结点。由于当前结点的状态进行了回滚,所以对于兄弟结点的那条路径来说该结点是“未被访问过”的状态。
- 步骤1中写的是从某一个结点开始遍历,而实际上本题需要对二维表中所有点都进行步骤1-6。
深度优先遍历及本题中的深度优先搜索:深度优先遍历与广度优先遍历为两种图遍历方式。深度优先遍历沿着结点向深处走直到不能深入为止。深度优先遍历时会使用一个额外的表来存储结点的访问信息,每次访问结点前都检查欲访问结点是否被访问过了,从而避免重复访问。本题中没有使用额外的表进行存储,而是直接将当前的board[i][j]置为一个不可能出现的值'\0'表示已被访问。递归前对其赋值而递归后对其进行还原,这样做能够使递归的下一层保存有“是否被访问过”这个信息,而当所有邻居结点的路径遍历完后如果还没找到正确路径则返回上层,返回前将board[i][j]还原,上一层会接着访问他的兄弟结点并认为认为这个结点未被访问过。(即“是否访问过”的记录表的状态有一个回滚的功能)
回溯的思想:回溯是指当发现这一条路径走不通时返回上一层后换下一条路走。如果换完当前点所有的路后都走不通则继续向上返回。返回上一层时需要保证状态也进行回滚。本题的解题思路中通过深度优先搜索来实现回溯思想。深度优先搜索本身是不可以实现回溯的,但是本题中对深度优先搜索稍作改变:取消了额外记录访问信息的表,而是通过二维表board[i][j]是否等于'\0'来表示当前结点是否被访问。而当前结点所有邻居结点的路都走不通时返回到上一层前将结点的board[i][j]也进行回滚。
要想弄懂回溯我们首先要搞懂递归,递归分为两步,先是递,然后才是归。当我们沿着当前坐标往下传递的时候,我们可以把当前坐标的值修改,然后回归到当前坐标的时候再把当前坐标的值复原,这就是回溯的过程。回溯, 引用自:sdwwld
代码
展开查看
class Solution {
private boolean t12DFS(char[][] board, String word, int row, int col, int currCharIndex){ // for t12
if(row<0 || row>=board.length || col<0 || col >=board[0].length || board[row][col]!=word.charAt(currCharIndex)) return false;
if(currCharIndex == word.length()-1) return true;
// 访问该结点,打印内容帮助理解
System.out.println("访问,row: "+row+", col: "+col+", value: "+board[row][col]);
// 递归访问其孩子结点
board[row][col] = '\0'; // 设置一个不可能出现的值表示该结点已经被访问过,并告诉孩子结点
boolean up = t12DFS(board,word,row-1,col,currCharIndex+1); // 上
boolean down = t12DFS(board,word,row+1,col,currCharIndex+1); // 下
boolean left = t12DFS(board,word,row,col-1,currCharIndex+1); // 左
boolean right = t12DFS(board,word,row,col+1,currCharIndex+1); // 右
// 上下左右路径都不正确,进行回溯,状态回滚
if(!(up || down ||left || right )) { //判断这个操作可能比直接赋值要慢,所以可以不判断,直接赋值。即不管当前结点的子节点有没有正确路径,都将该结点的状态回滚,缺点是路径信息丢失。
board[row][col] = word.charAt(currCharIndex);
System.out.println("回滚,row: "+row+", col: "+col+", value: "+board[row][col]);
}
return up || down ||left || right ;
}
public boolean exist(char[][] board, String word) { // t12 - 图的深度优先搜索+回溯思想
for(int row=0; row<board.length;row++)
for(int col=0;col<board[0].length;col++){
System.out.println("根节点: "+board[row][col]);
if(t12DFS(board,word,row,col,0)) return true;
}
return false;
}
}
T13. 机器人的运动范围
题目
难度:中等
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
提示:
1 <= n,m <= 100
0 <= k <= 20
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路1
展开查看
如下图所示,绿色为可达二红色为不可达。当k足够小时可达区域不连通,随着k变大可达区域一层一层扩大,不连通的区域也变得连通。

经验教训:刚拿到题目我就想,这不就是把所有格子遍历,然后满足条件的就答案+1吗?就算增加对称性的小trick,复杂度怎么说也是O(mn)不可能更小了,所以这个方案虽然粗暴但没有性能更好的方案了。但是很显然是错的。以后拿到题目之后要认真审题,题目中说的机器人总是从(0,0)开始走。所以当k比较小时尽管有些格子满足小于k的条件但是机器人不可达。
思路:本题实际上是一个可达性的检测。既然是原始点的可达性检测,那一个思路就直接从原始点开始遍历表格就行了,能遍历到的就是与原始点连通的。使用深度优先遍历(DFS)或者广度优先遍历(BFS)这两种遍历方式都可以。遍历时一个小trick是只需要往右方和下方走就行(可以证明本题中机器人从原点仅仅往右方和下方走就可以到达所有连通点),另一个小trick是剪枝(遇到障碍物立刻返回)。
代码1
展开查看
class Solution {
private int t13Count(int inputNum){ // for t13
int ans = 0;
while(inputNum!=0){
ans += inputNum % 10;
inputNum = inputNum /10;
}
return ans;
}
public int movingCount(int m, int n, int k) { // t13 法一: 图的遍历
//仅对原始结点进行的广度优先遍历
if(k==0) return 1;
int ans = 0;
boolean[][] visited = new boolean[m][n];
Queue<int[]> queue = new LinkedList<>();
// 访问根节点并将其入队
visited[0][0] = true;
ans ++;
queue.offer(new int[]{0,0});
while(!queue.isEmpty()){
// 将队首结点(已被访问过)出队,并将其满足条件的邻居结点访问后进行入队
int[] currentNode = queue.poll();
// 改进:对于邻居结点的访问,可以使用一个循环语句
int[] right = {currentNode[0],currentNode[1]+1};
if(right[1] < n && visited[right[0]][right[1]] == false &&
t13Count(right[0])+t13Count(right[1])<=k){// 访问并入队右边的格子
visited[right[0]][right[1]] = true;
ans++;
queue.offer(right);
}
int[] down = {currentNode[0]+1,currentNode[1]};
if(down[0]<m && visited[down[0]][down[1]] ==false && t13Count(down[0])+t13Count(down[1])<=k){// 访问并入队下边的格子
visited[down[0]][down[1]]=true;
ans++;
queue.offer(down);
}
}
return ans;
}
}
思路2
展开查看
本题实际上是一个可达性的检测。既然是原始点的可达性检测,那一个思路就直接从原始点开始递推可达到的格子。
通过观察可知,一个格子如果可达需满足:1. 左边或者上边可达;2. 坐标数字和小于k。
即avaliable[row][col]=(avaliable[row-1][col]||avaliable[row][col-1]) && sum(col)+sum(row)<=k.
代码2
展开查看
class Solution {
public int movingCount(int m, int n, int k) { // t13 法二: 递推。此方法比方法一要快并且内存消耗也小一点
if(k==0) return 1;
boolean[][] avaliable = new boolean[m][n];
int ans = 0;
avaliable[0][0] = true;
for(int row=0; row < m; row++)
for(int col=0; col<n; col++){
if(t13Count(row)+t13Count(col)>k) // 不满足条件则跳过
continue;
if(row-1 >=0) // 若上面可达,则当前也可达
avaliable[row][col] |= avaliable[row-1][col];
if(col-1>=0) // 若左面可达,则当前也可达
avaliable[row][col] |= avaliable[row][col-1];
ans += avaliable[row][col]?1:0; // 若该结点可达,则结果加1.由于是顺序遍历,所以不用考虑重复问题。
}
return ans;
}
}
T14- I. 剪绳子
题目
难度:中等
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]k[1]...*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 58
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/jian-sheng-zi-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路1
展开查看
求长度为n时切m段乘积最大值,只需要知道长度为n-1, n-2,...,n-k, ... 2 时的最大值即可,选出最大的dp[n-k]*k即为答案。可知道此思路动态规划的两个条件,即:
- 最优子结构(当一个问题的最优解包含了子问题的最优解时,称这个问题具有最优子结构)
- 重叠子问题(在问题的求解过程中,很多子问题的解将被多次使用)
于是可以使用动规来进行优化此思路,避免大量的重复计算导致资源浪费。
状态转移方程如下: dp[i] =max_{0<j<i-1}( max(长度为[i-j]时最大值*j))
注意,由于题目限制了至少要切一刀,所以dp[k]只能表示最优解而不表示长度为k时最大值。获得最大值还需要与k比较,即max(长度为[k]时最大值=max(dp[k],k)。
代码1
展开查看
class Solution {
public int cuttingRope(int n) { // 动规:自底向上;
if(n==2) return 1;
// 初始化状态表
int[] dp = new int[n+1]; //绳长为i的最佳答案
dp[2]=1; //注意边界
// 自底向上填表
for(int i=3; i<=n;i++){ //状态转移方程:dp[i] =max_{0<j<i-1}( max(长度为[i-j]时最大值*j))
for(int j =1; j<=i-2; j++){
dp[i] = Math.max(Math.max(dp[i-j],i-j)*j,dp[i]); //由于题目限制了至少要切一刀,所以dp[k]只能表示最优解而不表示长度为k时最大值。获得最大值还需要与与k比较
}
}
return dp[n];
}
}
展开查看
class Solution {
public int recurrCutting(int n, int[] dp){ // for t14-1
if(n==2)
return 1;
for(int j=1; j<=n-2; j++){
if(dp[n-j]==0) dp[n-j] = recurrCutting(n-j,dp);
dp[n] = Math.max(Math.max(dp[n-j],n-j)*j,dp[n]);
}
return dp[n];
}
public int cuttingRope(int n) {// t14-1 方法二:动规(自顶向下备忘录) 7min
int[] dp = new int[n+1];//绳长为i的最佳答案
// 数组默认初始化为0
return recurrCutting(n,dp);
}
}
思路2
代码2
展开查看
class Solution {
public int cuttingRope(int n) {
if(n <= 3) return n - 1;
int a = n / 3, b = n % 3;
if(b == 0) return (int)Math.pow(3, a);
if(b == 1) return (int)Math.pow(3, a - 1) * 4;
return (int)Math.pow(3, a) * 2;
}
}
T14- II. 剪绳子 II
题目
难度:中等
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]k[1]...*k[m - 1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 1000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/jian-sheng-zi-ii-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
展开查看
与T14-1的唯一区别就是大数越界情况下的求余问题。由于int所表达的范围有限,当答案超出范围时将会产生错误的结果。使用BigInteger解决这个问题。
代码
展开查看
import java.math.BigInteger;
class Solution {
public int cuttingRope(int n) { // t14-2 方法一:动规(自底向上),与t14-1 方法一 一致,仅仅将变量更改为BigInteger
if(n==2) return 1;
// 初始化状态表
BigInteger[] dp = new BigInteger[n+1]; //绳长为i的最佳答案
Arrays.fill(dp,BigInteger.valueOf(0));
dp[2]=BigInteger.ONE; //注意边界
// 自底向上填表
for(int i=3; i<=n;i++){ //状态转移方程:dp[i] =max_{0<j<i-1}( max(长度为[i-j]时最大值*j))
for(int j =1; j<=i-2; j++){
dp[i] = dp[i].max(dp[i-j].multiply(BigInteger.valueOf(j)).max(BigInteger.valueOf((i-j)*j))); //由于题目限制了至少要切一刀,所以dp[k]只能表示最优解而不表示长度为k时最大值。获得最大值还需要与与k比较
}
}
return dp[n].mod(BigInteger.valueOf(1000000007)).intValue();
}
}
T15. 二进制中1的个数
题目
难度:简单
请实现一个函数,输入一个整数(以二进制串形式),输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
提示:
输入必须是长度为 32 的 二进制串 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/er-jin-zhi-zhong-1de-ge-shu-lcof
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路1
展开查看
对输入的二进制数进行尾部判断并截去尾部,重复直至二进制数变为0为止。
判断二进制数末尾是否为零可以使用 n&1来判断,截去尾部可以通过 n=n>>>1来操作。>>>为无符号右移。
注意,输入虽然为int类型,但是其本质(对计算机来说)也是一个32位的二进制数而已,只不过平时在做十进制操作符运算符计算时自动将其解析为十进制。我们想直接对其进行二进制操作则使用二进制操作符 & >> 等就可以了。
此外,在数字前面加不同符合表示不同进制:
- 二进制 0b
- 八进制 0
- 十进制
- 十六进制 ox
代码1
展开查看
class Solution {
public int hammingWeight(int n) { // t15 法一: 循环判断最后一位并截去
// you need to treat n as an unsigned value
int res =0;
while(n!=0){
res += n & 1;
n >>>= 1;
}
return res;
}
}
思路2
展开查看
巧用 n&(n-1)
根据二进制数的性质,
- n-1解析:二进制数字
n最右边的1变成0,此1右边的0都变成1。 - n&(n−1) 解析: 二进制数字
n最右边的1变成0,其余不变。
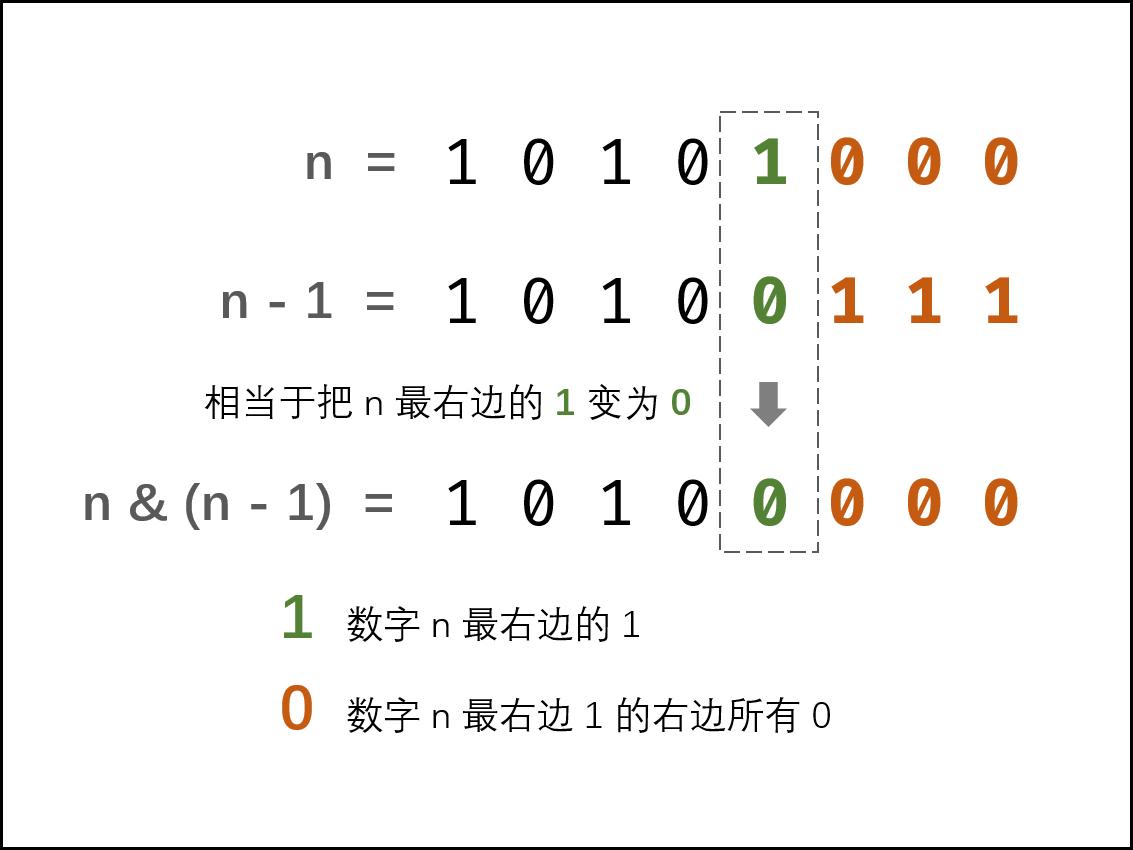
代码2
展开查看
class Solution {
public int hammingWeight(int n) { // t15 法二:巧用 n&(n-1)
int res = 0;
while(n!=0){
res ++;
n&=(n-1);
}
return res;
}
}
T0. Markdown使用样例
题目
使用Markdown书写行内代码和区块代码。
思路
展开查看
这是一个行内代码Java;区块代码如下所示。
代码
展开查看
class Solution {
public boolean example(String word) {
// 标签与正文之间需要空行
}
}





