梯度下降法

给定损失函数，随机初始化一个位置（w0,b0）,在该位置，沿着梯度方向是损失函数下降最快的方向，具体的证明是在该点的局部将函数进行泰勒展开，并取零次项以及一次项对函数进行近似之后，可以将目标函数化简为常数项以及两个向量相加的形式，为了使目标函数最小，则需要使得向量中的可变者与原来的向量（梯度组成的向量）方向相反，大小则是通过学习率设置的，也就是梯度下降的方向。

 

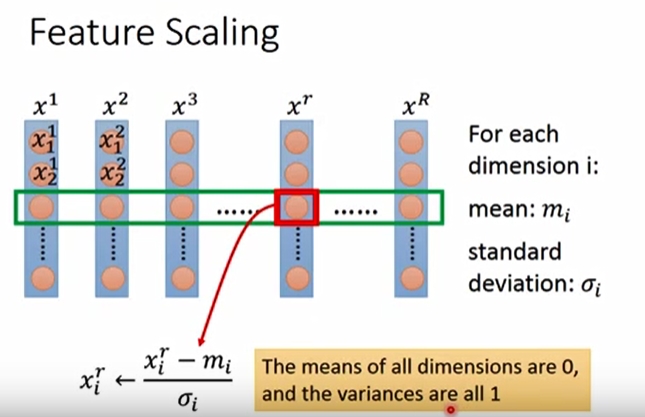
另外，在进行梯度下降时，需要注意对输入变量的归一化（feature scaling）。将所有的输入都归一化至同样的尺度，然后再进行梯度下降的寻优，使得收敛更快速。

 

在对损失函数进行设计的时候，加入正则化项可以使函数更加平滑，也就是说某个变量变化时对损失函数造成的波动越小，也就是我们最终的损失函数是包含两项的：error+smooth，要两者兼顾，才能收敛到较好的效果；

 

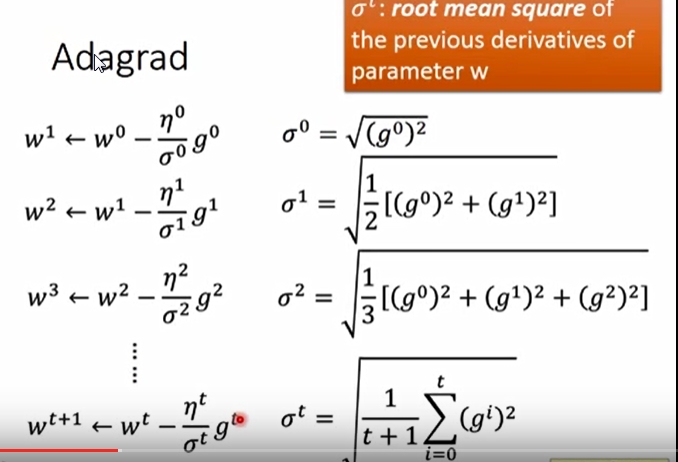
常见的比较好的梯度下降算法有：Adagrad以及SGD，Adagrad考虑了从开始到当前迭代时的所有梯度值（从数学上推导，其实是综合考量了一次与二次导数），SGD则是只考虑摸个sample的梯度下降方向。