使用Java实现二叉树的添加,删除,获取以及遍历
一段来自百度百科的对二叉树的解释:
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
一棵深度为k,且有2^k-1个节点的二叉树,称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树,至少有2k-1个叶子节点,至多有2k-1个节点。
二叉树的结构:
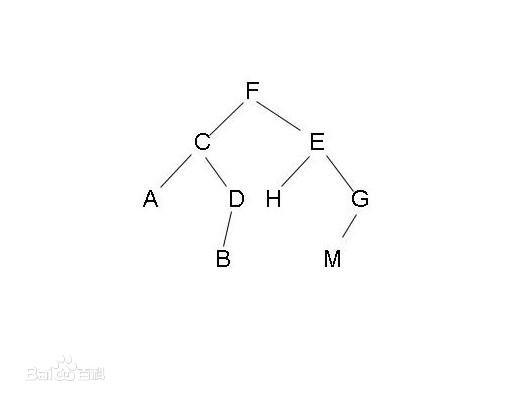
二叉树节点的声明:
static final class Entry<T extends Comparable<T>>{ //保存的数据 private T item; //左子树 private Entry<T> left; //右子树 private Entry<T> right; //父节点 private Entry<T> parent; Entry(T item,Entry<T> parent){ this.item = item; this.parent = parent; } }
类属性:
//根节点 private Entry<T> root; //数据量 private int size = 0;
二叉树添加数据:
/** * 添加元素 * @param item 待添加元素 * @return 已添加元素 */ public T put(T item){ //每次添加数据的时候都是从根节点向下遍历 Entry<T> t = root; if (t == null){ //当前的叉树树的为空,将新节点设置为根节点,父节点为null root = new Entry<>(item,null);
size++; return root.item; } //自然排序结果,如果传入的数据小于当前节点返回-1,大于当前节点返回1,否则返回0 int ret = 0; //记录父节点 Entry<T> p = t; while (t != null){ //与当前节点比较 ret = item.compareTo(t.item); p = t; //插入节点比当前节点小,把当前节点设置为左子节点,然后与左子比较,以此类推找到合适的位置 if (ret < 0) t = t.left; //大于当前节点 else if (ret > 0) t = t.right; else { //相等就把旧值覆盖掉 t.item = item; return t.item; } } //创建新节点 Entry<T> e = new Entry<>(item,p); //根据比较结果将新节点放入合适的位置 if (ret < 0) p.left = e; else p.right = e;
size++; return e.item; }
在put的过程中,使用Comparable<T>中的compareTo来比较两个元素的大小的,所以在二叉树中存储的元素必须要继承Comparable<T> 类,覆写compareTo方法。
二叉树删除数据
/** * 删除元素 * 删除元素如果细分的话,可以分为4中:没有子节点,只有左节点,只有右节点,有两个子节点 * 1)没有子节点这种情况比较简单,直接删除就可以了 * 2)只有左节点或右节点,这两种情况处理方式是一致的,只是方向相反,所以在一起讲了, * 将删除节点的父节点的左节点(右节点)指向删除节点的子节点,将左节点(右节点)指向删除节点的父节点 * 3)有两个子节点,这种情况相对来说比较复杂一点: * 找到删除节点的前驱节点或后继节点,然后将前驱或后继节点的值赋给删除节点,然后将前驱或后继节点删除。本质是删除前驱或后继节点 * 前驱节点的特点: * 1)删除的左子节点没有右子节点,那么左子节点即为前驱节点 * 2)删除节点的左子节点有右子节点,那么最右边的最后一个节点即为前驱节点 * 后继节点的特点: * 与前驱节点刚好相反,总是右子节点,或则右子节点的最左子节点;例如:删除节点为c ,那么前驱节点为 m,后继节点为n * a * / \ * b c * / \ / \ * d e f g * / \ / \ / \ / \ * @param item 删除元素 h i j k l m n o * @return 删除结果 */ public boolean remove(T item){ //获取删除节点 Entry<T> delEntry = getEntry(item); if (delEntry == null) return false; //删除节点的父节点 Entry<T> p = delEntry.parent; size--; //情况1:没有子节点 if (delEntry.left == null && delEntry.right == null){ //删除节点为根节点 if (delEntry == root){ root = null; }else {//非根节点 //删除的是父节点的左节点 if (delEntry == p.left){ p.left = null; }else {//删除右节点 p.right = null; } } //情况2:删除的节点只有左节点 }else if (delEntry.right == null){ Entry<T> lc = delEntry.left; //删除的节点为根节点,将删除节点的左节点设置成根节点 if (p == null) { lc.parent = null; root = lc; } else {//非根节点 if (delEntry == p.left){//删除左节点 p.left = lc; }else {//删除右节点 p.right = lc; } lc.parent = p; } //情况3:删除节点只有右节点 }else if (delEntry.left == null){ Entry<T> rc = delEntry.right; //删除根节点 if (p == null) { rc.parent = null; root = rc; }else {//删除非根节点 if (delEntry == p.left) p.left = rc; else p.right = rc; rc.parent = p; } //情况4:删除节点有两个子节点 }else {//有两个节点,找到后继节点,将值赋给删除节点,然后将后继节点删除掉即可 Entry<T> successor = successor(delEntry);//获取到后继节点 delEntry.item = successor.item; //后继节点为右子节点 if (delEntry.right == successor){ //右子节点有右子节点 if (successor.right != null) { delEntry.right = successor.right; successor.right.parent = delEntry; }else {//右子节点没有子节点 delEntry.right = null; } }else {//后继节点必定是左节点 successor.parent.left = null; } return true; } //让gc回收 delEntry.parent = null; delEntry.left = null; delEntry.right = null; return true; } /** * 获取节点节点 * @param item 获取节点 * @return 获取到的节点,可能为null */ private Entry<T> getEntry(T item){ Entry<T> t = root; int ret; //从根节点开始遍历 for (;t != null;){ ret = item.compareTo(t.item); if (ret < 0) t = t.left; else if (ret > 0) t = t.right; else return t; } return null; } /** * 查找后继节点 * @param delEntry 删除节点 * @return 后继节点 */ private Entry<T> successor(Entry<T> delEntry) { Entry<T> r = delEntry.right;//r节点必定不为空 while (r.left != null){ r = r.left; } return r; }
二叉树获取节点
/** * 判断是否存在该元素 * @param item 查找元素 * @return 结果 */ public boolean contains(T item){ return getEntry(item) != null; } /** * 获取节点节点 * @param item 获取节点 * @return 获取到的节点,可能为null */ private Entry<T> getEntry(T item){ Entry<T> t = root; int ret; //从根节点开始遍历 for (;t != null;){ ret = item.compareTo(t.item); if (ret < 0) t = t.left; else if (ret > 0) t = t.right; else return t; } return null; }
因为我这个例子是存储一个元素,获取到的元素和传进去的元素是一致的,所以我用contains方法来判断返回true即表示获取成功了,不返回获取到的结果了。当然,如果将entry存储的元素改为kv形式的话,就可以使用get方法了。
二叉树的遍历
二叉树的遍历可以分为三种:前序遍历、中序遍历和后续遍历,其中中序遍历是最常用的遍历方式,因为它遍历出来的结果的升序的。
前序遍历:
/** * 前序遍历 * @param e 开始遍历元素 */ public void prevIterator(Entry<T> e){ if (e != null) { System.out.print(e.item + " "); prevIterator(e.left); prevIterator(e.right); } }
中序遍历:
/** * 中序遍历 * @param e */ public void midIterator(Entry<T> e){ if (e != null){ midIterator(e.left); System.out.print(e.item + " "); midIterator(e.right); } }
后序遍历:
/** * 后续遍历 * @param e 开始遍历元素 */ public void subIterator(Entry<T> e){ if (e != null) { subIterator(e.left); subIterator(e.right); System.out.print(e.item + " "); } }
demo完整的代码:也可以到我的github中下载代码:https://github.com/rainple1860/MyCollection
package com.rainple.collections; /** * 二叉树 * @param <T> */ public class BinaryTree<T extends Comparable<T>> { //根节点 private Entry<T> root; //数据量 private int size = 0; public BinaryTree(){} /** * 添加元素 * @param item 待添加元素 * @return 已添加元素 */ public T put(T item){ //每次添加数据的时候都是从根节点向下遍历 Entry<T> t = root; size++; if (t == null){ //当前的叉树树的为空,将新节点设置为根节点,父节点为null root = new Entry<>(item,null); return root.item; } //自然排序结果,如果传入的数据小于当前节点返回-1,大于当前节点返回1,否则返回0 int ret = 0; //记录父节点 Entry<T> p = t; while (t != null){ //与当前节点比较 ret = item.compareTo(t.item); p = t; //插入节点比当前节点小,把当前节点设置为左子节点,然后与左子比较,以此类推找到合适的位置 if (ret < 0) t = t.left; //大于当前节点 else if (ret > 0) t = t.right; else { //相等就把旧值覆盖掉 t.item = item; return t.item; } } //创建新节点 Entry<T> e = new Entry<>(item,p); //根据比较结果将新节点放入合适的位置 if (ret < 0) p.left = e; else p.right = e; return e.item; } public void print(){ midIterator(root); } /** * 中序遍历 * @param e */ public void midIterator(Entry<T> e){ if (e != null){ midIterator(e.left); System.out.print(e.item + " "); midIterator(e.right); } } /** * 获取根节点 * @return 根节点 */ public Entry<T> getRoot(){return root;} /** * 前序遍历 * @param e 开始遍历元素 */ public void prevIterator(Entry<T> e){ if (e != null) { System.out.print(e.item + " "); prevIterator(e.left); prevIterator(e.right); } } /** * 后续遍历 * @param e 开始遍历元素 */ public void subIterator(Entry<T> e){ if (e != null) { subIterator(e.left); subIterator(e.right); System.out.print(e.item + " "); } } /** * 获取节点节点 * @param item 获取节点 * @return 获取到的节点,可能为null */ private Entry<T> getEntry(T item){ Entry<T> t = root; int ret; //从根节点开始遍历 for (;t != null;){ ret = item.compareTo(t.item); if (ret < 0) t = t.left; else if (ret > 0) t = t.right; else return t; } return null; } /** * 判断是否存在该元素 * @param item 查找元素 * @return 结果 */ public boolean contains(T item){ return getEntry(item) != null; } /** * 删除元素 * 删除元素如果细分的话,可以分为4中:没有子节点,只有左节点,只有右节点,有两个子节点 * 1)没有子节点这种情况比较简单,直接删除就可以了 * 2)只有左节点或右节点,这两种情况处理方式是一致的,只是方向相反,所以在一起讲了, * 将删除节点的父节点的左节点(右节点)指向删除节点的子节点,将左节点(右节点)指向删除节点的父节点 * 3)有两个子节点,这种情况相对来说比较复杂一点: * 找到删除节点的前驱节点或后继节点,然后将前驱或后继节点的值赋给删除节点,然后将前驱或后继节点删除。本质是删除前驱或后继节点 * 前驱节点的特点: * 1)删除的左子节点没有右子节点,那么左子节点即为前驱节点 * 2)删除节点的左子节点有右子节点,那么最右边的最后一个节点即为前驱节点 * 后继节点的特点: * 与前驱节点刚好相反,总是右子节点,或则右子节点的最左子节点;例如:删除节点为c ,那么前驱节点为 m,后继节点为n * a * / \ * b c * / \ / \ * d e f g * / \ / \ / \ / \ * @param item 删除元素 h i j k l m n o * @return 删除结果 */ public boolean remove(T item){ //获取删除节点 Entry<T> delEntry = getEntry(item); if (delEntry == null) return false; //删除节点的父节点 Entry<T> p = delEntry.parent; size--; //情况1:没有子节点 if (delEntry.left == null && delEntry.right == null){ //删除节点为根节点 if (delEntry == root){ root = null; }else {//非根节点 //删除的是父节点的左节点 if (delEntry == p.left){ p.left = null; }else {//删除右节点 p.right = null; } } //情况2:删除的节点只有左节点 }else if (delEntry.right == null){ Entry<T> lc = delEntry.left; //删除的节点为根节点,将删除节点的左节点设置成根节点 if (p == null) { lc.parent = null; root = lc; } else {//非根节点 if (delEntry == p.left){//删除左节点 p.left = lc; }else {//删除右节点 p.right = lc; } lc.parent = p; } //情况3:删除节点只有右节点 }else if (delEntry.left == null){ Entry<T> rc = delEntry.right; //删除根节点 if (p == null) { rc.parent = null; root = rc; }else {//删除非根节点 if (delEntry == p.left) p.left = rc; else p.right = rc; rc.parent = p; } //情况4:删除节点有两个子节点 }else {//有两个节点,找到后继节点,将值赋给删除节点,然后将后继节点删除掉即可 Entry<T> successor = successor(delEntry);//获取到后继节点 delEntry.item = successor.item; //后继节点为右子节点 if (delEntry.right == successor){ //右子节点有右子节点 if (successor.right != null) { delEntry.right = successor.right; successor.right.parent = delEntry; }else {//右子节点没有子节点 delEntry.right = null; } }else {//后继节点必定是左节点 successor.parent.left = null; } return true; } //让gc回收 delEntry.parent = null; delEntry.left = null; delEntry.right = null; return true; } /** * 查找后继节点 * @param delEntry 删除节点 * @return 后继节点 */ private Entry<T> successor(Entry<T> delEntry) { Entry<T> r = delEntry.right;//r节点必定不为空 while (r.left != null){ r = r.left; } return r; } public int size(){return size;} public boolean isEmpty(){return size == 0;} public void clear(){ clear(getRoot()); root = null; } private void clear(Entry<T> e){ if (e != null){ clear(e.left); e.left = null; clear(e.right); e.right = null; } } static final class Entry<T extends Comparable<T>>{ //保存的数据 private T item; //左子树 private Entry<T> left; //右子树 private Entry<T> right; //父节点 private Entry<T> parent; Entry(T item,Entry<T> parent){ this.item = item; this.parent = parent; } } }
测试代码示例:
public static void main(String[] args) { BinaryTree<Integer> binaryTree = new BinaryTree<>(); //放数据 binaryTree.put(73); binaryTree.put(22); binaryTree.put(532); binaryTree.put(62); binaryTree.put(72); binaryTree.put(243); binaryTree.put(42); binaryTree.put(3); binaryTree.put(12); binaryTree.put(52); System.out.println("size: " + binaryTree.size()); binaryTree.put(52); System.out.println("添加相同元素后的size: " + binaryTree.size()); //判断数据是否存在 System.out.println("数据是否存在:" + binaryTree.contains(12)); //中序遍历 System.out.print("中序遍历结果: "); binaryTree.midIterator(binaryTree.getRoot()); System.out.println(); //前序遍历 System.out.print("前遍历结果: "); binaryTree.prevIterator(binaryTree.getRoot()); System.out.println(); //后序遍历 System.out.print("后续遍历结果: "); binaryTree.subIterator(binaryTree.getRoot()); //删除数据 System.out.println(); binaryTree.remove(62); System.out.println("删除数据后判断是否存在:" + binaryTree.contains(62)); //清空二叉树 binaryTree.clear(); System.out.print("清空数据后中序遍历: "); binaryTree.midIterator(binaryTree.getRoot()); }
测试结果:
size: 10 添加相同元素后的size: 10 数据是否存在:true 中序遍历结果: 3 12 22 42 52 62 72 73 243 532 前遍历结果: 73 22 3 12 62 42 52 72 532 243 后续遍历结果: 12 3 52 42 72 62 22 243 532 73 删除数据后判断是否存在:false 清空数据后中序遍历:
纯手写的demo,有什么错误的地方欢迎指正,谢谢大家的阅读!!!
欢迎大家关注公众号: 【java解忧杂货铺】,里面会不定时发布一些技术博客;关注即可免费领取大量最新,最流行的技术教学视频:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号