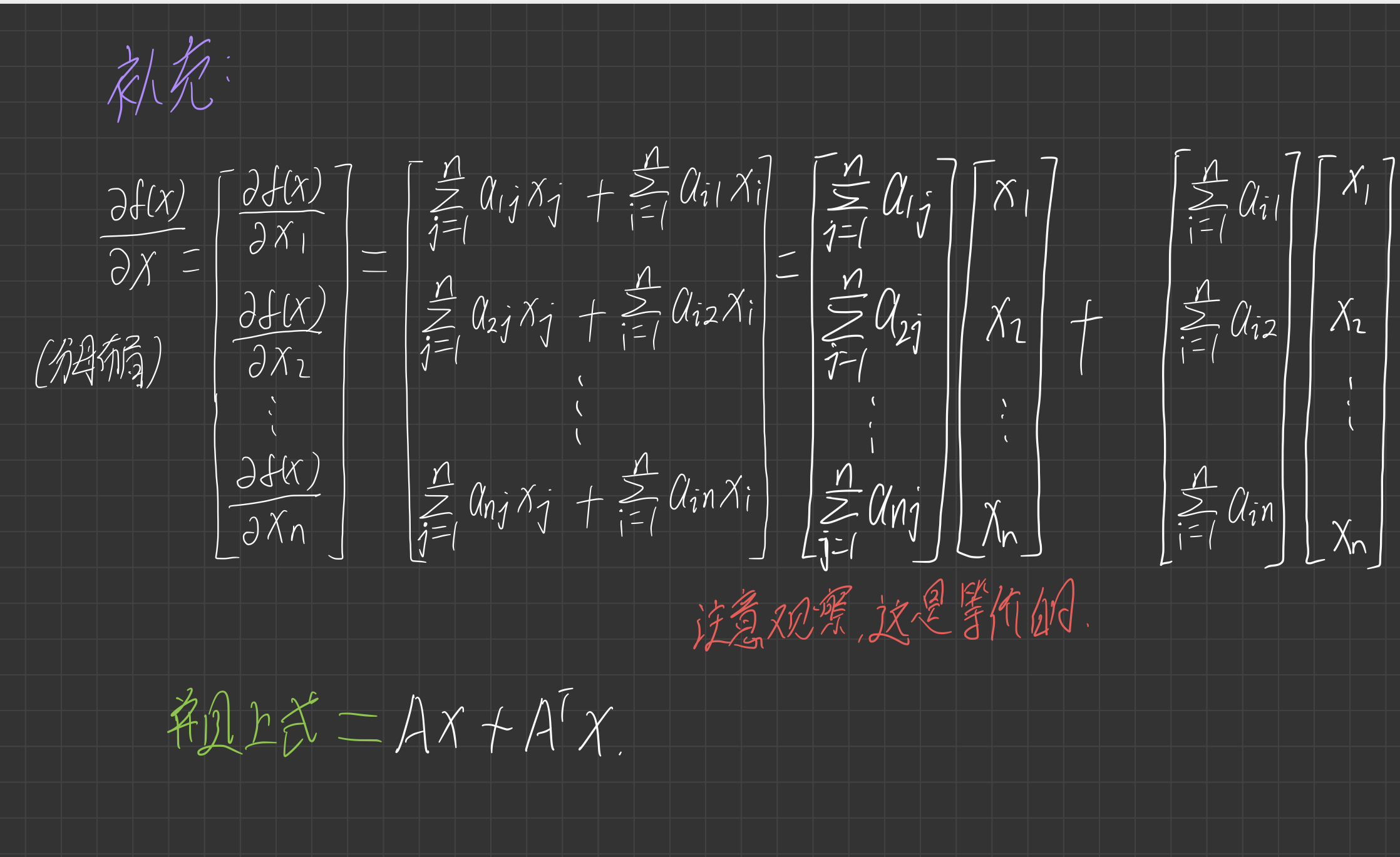特别感谢一下两名作者的链接:矩阵求导的本质与分子布局、分母布局的本质(矩阵求导——本质篇)
机器学习中的矩阵向量求导(一) 求导定义与求导布局 - 刘建平Pinard
本文对上述两篇文章做一个小小的总结,当然主要还是借鉴甚至是复制前人的思想,在此再次表达我的感激,感谢两位作者无私的分享。
再贴上大神的GitHub链接ljpzzz/machinelearning: My blogs and code for machine learning.
注意,本文若无特殊说明,向量均为列向量表示,如\(\pmb{x}=[x_1,x_2,\cdots,x_n]^T\)
一、函数与标量、向量、矩阵
考虑一个函数
\[function(input)
\]
针对 \(function\) 的类型、\(input\) 的类型,我们可以将这个函数 \(function\) 分为不同的种类。
| function \ input |
标量变元 |
向量变元 |
矩阵变元 |
| 实值标量函数 |
\(f(x)\) |
\(f(\pmb{x})\) |
\(f(\pmb X)\) |
| 实向量函数 |
\(\pmb{f}(x)\) |
\(\pmb{f}(\pmb x)\) |
\(\pmb{f}(\pmb X)\) |
| 实矩阵函数 |
\(\pmb{F}(x)\) |
\(\pmb{F}(\pmb x)\) |
\(\pmb{F}(\pmb X)\) |
1、\(function\)是一个标量
我们称 \(function\) 是一个实值标量函数。用细体小写字母 \(f\) 表示。
1.1 \(input\)是一个标量
我们称 \(function\) 的变元是标量。用细体小写字母 \(x\) 表示。这就是我们之前主要接触的,所以也就没有什么特别要讲的~
例1:
\[f(x)=x+2 \tag{e.g.1}
\]
1.2 \(input\) 是一个向量
我们称 \(function\) 的变元是向量。用粗体小写字母 \(\pmb{x}\) 表示。对于这种情况,我们其实可以理解为输入为多元变量。这种情况其实比较重要,因为在机器学习里往往根据Loss函数计算损失,输入是向量,而输出的则是标量。
例2:设 \(\pmb{x}=[x_1,x_2,x_n]^T\)
\[f(\pmb{x})=a_1x_1^2+a_2x_2^2+a_3x_3^2+a_4x_1x_2 \tag{e.g.2}
\]
1.3 \(input\) 是一个矩阵
我们称 \(function\) 的变元是矩阵。用粗体大写字母 \(\pmb{X}\) 表示。
例3:设 \(\pmb{X}_{3\times 2}=(x_{ij})_{i=1,j=1}^{3,2}\)
\[f(\pmb{X})=a_1x_{11}^2+a_2x_{12}^2+a_3x_{21}^2+a_4x_{22}^2+a_5x_{31}^2+a_6x_{32}^2 \tag{e.g.3}
\]
2、\(function\) 是一个向量
我们称 \(function\) 是一个实向量函数 。用粗体小写字母 \(\pmb{f}\) 表示。
含义:\(\pmb{f}\) 是由若干个 \(f\) 组成的一个向量。
同样地,变元分三种:标量、向量、矩阵。这里的符号仍与上面相同。向量函数与标量函数稍微有所不同,我们可以将其理解为多个标量函数按照一定格式组织在了一起即可。
2.1 标量变元
例4:
\[\pmb{f}_{3\times1}(x)= \left[ \matrix{ f_1(x)\\ f_2(x)\\ f_3(x)\\ } \right] = \left[ \matrix{ x+1\\ 2x+1\\ 3x^2+1 } \right] \tag{e.g.4}
\]
2.2 向量变元
例5:设\(\pmb{x}=[x_1,x_2,x_n]^T\)
\[\pmb{f}_{3\times1}(\pmb{x})= \left[ \matrix{ f_1(\pmb{x})\\ f_2(\pmb{x})\\ f_3(\pmb{x})\\ } \right] = \left[ \matrix{ x_{1}+x_{2}+x_{3}\\ x_{1}^2+2x_{2}+2x_{3}\\ x_{1}x_{2}+x_{2}+x_{3} } \right] \tag{e.g.5}
\]
2.3 矩阵变元
例6:设\(\pmb{X}_{3\times 2}=(x_{ij})_{i=1,j=1}^{3,2}\)
\[\pmb{f}_{3\times1}(\pmb{X})= \left[ \matrix{ f_1(\pmb{X})\\ f_2(\pmb{X})\\ f_3(\pmb{X})\\ } \right] = \left[ \matrix{ x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\ x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}+x_{11}x_{12}\\ 2x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}+x_{11}x_{12} } \right] \tag{e.g.6}
\]
3、\(function\) 是一个矩阵
我们称 \(functionfunction\) 是一个实矩阵函数。用粗体大写字母 \(\pmb{F}\) 表示。
含义:\(\pmb{F}\) 是由若干个 \(f\) 组成的一个矩阵。
同样地,变元分三种:标量、向量、矩阵。这里的符号仍与上面相同。
3.1 标量变元
例7:
\[\pmb{F}_{3\times2}(x)= \left[ \matrix{ f_{11}(x) & f_{12}(x)\\ f_{21}(x) & f_{22}(x)\\ f_{31}(x) & f_{32}(x)\\ } \right] = \left[ \matrix{ x+1 & 2x+2\\ x^2+1 & 2x^2+1\\ x^3+1 & 2x^3+1 } \right] \tag{e.g.7}
\]
3.2 变量变元
例8:设\(\pmb{x}=[x_1,x_2,x_n]^T\)
\[\pmb{F}_{3\times2}(\pmb{x})= \left[ \matrix{ f_{11}(\pmb{x}) & f_{12}(\pmb{x})\\ f_{21}(\pmb{x}) & f_{22}(\pmb{x})\\ f_{31}(\pmb{x}) & f_{32}(\pmb{x})\\ } \right] = \left[ \matrix{ 2x_{1}+x_{2}+x_{3} & 2x_{1}+2x_{2}+x_{3} \\ 2x_{1}+2x_{2}+x_{3} & x_{1}+2x_{2}+x_{3} & \\ 2x_{1}+x_{2}+2x_{3} & x_{1}+2x_{2}+2x_{3} & } \right] \tag{e.g.8}
\]
3.3 矩阵变元
例9:设\(\pmb{X}_{3\times 2}=(x_{ij})_{i=1,j=1}^{3,2}\)
\[\begin{align*} \pmb{F}_{3\times2}(\pmb{X})&= \left[ \matrix{ f_{11}(\pmb{X}) & f_{12}(\pmb{X})\\ f_{21}(\pmb{X}) & f_{22}(\pmb{X})\\ f_{31}(\pmb{X}) & f_{32}(\pmb{X})\\ } \right]\\\\ &= \left[ \matrix{ x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} & 2x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\ 3x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} & 4x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32}\\ 5x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} & 6x_{11}+x_{12}+x_{21}+x_{22}+x_{31}+x_{32} } \right] \end{align*} \tag{e.g.9}
\]
二、矩阵求导的本质
本质: \(function\) 中的每个 \(f\) 分别都对变元中的每个元素逐个求偏导,只不过写成了向量、矩阵形式而已。
例10:定义法求解导数问题
\[f(x_1,x_2,x_3)=x_1^2+x_1x_2+x_2x_3 \tag{e.g.10}
\]
我们可以将 \(f\) 对 \(x_1, x_2, x_3\) 的偏导分别求出来,即:
\[\left\{ \begin{align*} \frac{\partial f}{\partial x_1} & = 2x_1+x_2 \\ \frac{\partial f}{\partial x_2} & = x_1+x_3 \\ \frac{\partial f}{\partial x_3} & = x_2 \end{align*} \right.
\]
我们可以把得出的结果写成列向量形式:
\[\frac{\partial f(\pmb{x})}{\partial \pmb{x}_{3\times1}}= \left[ \matrix{ \frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\\ \frac{\partial f}{\partial x_3}\\ } \right] = \left[ \matrix{ 2x_1+x_2\\ x_1+x_3\\ x_2 } \right] \tag{1}
\]
一个矩阵求导以列向量形式展开的雏形就出现了。
当然我们也可以以行向量形式展开:
\[\frac{\partial f(\pmb{x})}{\partial \pmb{x}_{3\times1}^T}= \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \frac{\partial f}{\partial x_3} \right] = \left[ 2x_1+x_2, x_1+x_3, x_2 \right] \tag{2}
\]
矩阵求导的结果的形式是以列向量还是行向量其实这个无所谓,主要是确定好一个布局之后,按照这个规范就可以方便地进行统一的运算
至于这 \(m \times n\) 个结果的布局,是写成行向量,还是列向量,还是写成矩阵,就是接下来的布局问题了。
三、矩阵求导结果的布局
分子布局,求导结果维数以分子为主。
分母布局,求导结果维数以分母为主。
对于分子布局和分母布局的结果来说,两者相差一个转置。
这样,对于标量对向量或者矩阵求导,向量或者矩阵对标量求导这4种情况,对应的分子布局和分母布局的排列方式已经确定了。
稍微麻烦的就是向量对向量求导:
前提:m维列向量 \(\mathbf{y}\),n维列向量 \(\mathbf{x}\)
对于上述它的求导结果在分子布局和分母布局各是什么呢???
对于这两个向量求导,一共有mn个标量对标量的求导。求导的结果一般排列为一个矩阵。
分子布局
如果是分子布局,则矩阵的第一个维度以分子为准,即结果是一个 \(m \times n\) 的矩阵,如下:
\[\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \left( \begin{array}{ccc} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \ldots & \frac{\partial y_1}{\partial x_n}\\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2} & \ldots & \frac{\partial y_2}{\partial x_n}\\ \vdots& \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1}& \frac{\partial y_m}{\partial x_2} & \ldots & \frac{\partial y_m}{\partial x_n} \end{array} \right)
\]
上边这个按分子布局的向量对向量求导的结果矩阵,我们一般叫做雅克比 (Jacobian)矩阵。有的资料上会使用 \(\frac{\partial\mathbf{y}}{\partial{\mathbf{x}^T}}\) 来定义雅克比矩阵,意义是一样的。如下,分子是列向量形式,分母是行向量形式,结果就是 \(2 \times 3\) 的矩阵了:
\[\frac{\partial \pmb{f}_{2\times1}(\pmb{x})}{\partial \pmb{x}^T_{3\times1}}= \left[ \matrix{ \frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& \frac{\partial f_1}{\partial x_3}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& \frac{\partial f_2}{\partial x_3}} \right]_{2\times 3} \tag{3}
\]
分母布局
如果是分母布局,则矩阵的第一个维度以分母为准,即结果是一个 \(n \times m\) 的矩阵,如下:
\[\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \left( \begin{array}{ccc} \frac{\partial y_1}{\partial x_1}& \frac{\partial y_2}{\partial x_1}& \ldots & \frac{\partial y_m}{\partial x_1}\\ \frac{\partial y_1}{\partial x_2}& \frac{\partial y_2}{\partial x_2} & \ldots & \frac{\partial y_m}{\partial x_2}\\ \vdots& \vdots & \ddots & \vdots \\ \frac{\partial y_1}{\partial x_n}& \frac{\partial y_2}{\partial x_n} & \ldots & \frac{\partial y_m}{\partial x_n} \end{array} \right)
\]
上边这个按分母布局的向量对向量求导的结果矩阵,我们一般叫做梯度矩阵。有的资料上会使用 \(\frac{\partial\mathbf{y}^T}{\partial{\mathbf{x}}}\) 来定义梯度矩阵,意义是一样的。如下,分母是列向量形式,分子是行向量形式,结果就是 \(3 \times 2\) 的矩阵了:
\[\frac{\partial \pmb{f}^T_{2\times1}(\pmb{x})}{\partial \pmb{x}_{3\times1}}= \left[ \matrix{ \frac{\partial f_1}{\partial x_1}& \frac{\partial f_2}{\partial x_1} \\ \frac{\partial f_1}{\partial x_2}& \frac{\partial f_2}{\partial x_2} \\ \frac{\partial f_1}{\partial x_3}& \frac{\partial f_2}{\partial x_3} } \right]_{3\times 2} \tag{4}
\]
有了布局的概念,我们对于上面5种求导类型,可以各选择一种布局来求导。但是对于某一种求导类型,不能同时使用分子布局和分母布局求导。
但是在机器学习算法原理的资料推导里,我们并没有看到说正在使用什么布局,也就是说布局被隐含了,这就需要自己去推演,比较麻烦。但是一般来说我们会使用一种叫混合布局的思路,即如果是向量或者矩阵对标量求导,则使用分子布局为准,如果是标量对向量或者矩阵求导,则以分母布局为准。
总结如下:
| 自变量\因变量 |
标量y |
列向量\(\mathbf y\) |
矩阵\(\mathbf Y\) |
| 标量x |
/ |
\(\frac{\partial\mathbf{y}}{\partial{x}}\)
分子布局:m维列向量(默认布局)
分母布局:m维行向量 |
\(\frac{\partial\mathbf{Y}}{\partial{{x}}}\)
分子布局:\(m\times n\) 矩阵(默认布局)
分母布局:\(n\times m\) 矩阵 |
| 列向量 \(\mathbf x\) |
\(\frac{\partial{y}}{\partial{\mathbf x}}\)
分子布局:n维行向量
分母布局:n维列向量(默认布局) |
\(\frac{\partial\mathbf{y}}{\partial{\mathbf{x}}}\)
分子布局:\(m\times n\)雅克比矩阵(默认布局)
分母布局:\(n\times m\)梯度矩阵 |
/ |
| 矩阵 |
\(\frac{\partial y}{\partial{\mathbf{X}}}\)
分子布局:\(n\times m\) 矩阵
分母布局:\(m\times n\) 矩阵(默认布局) |
/ |
/ |
涉及矩阵的求导
如上,我们只讨论了五种情况,对于标量对标量求导下面不做讲解,只补充向量与矩阵之间的求导及矩阵对矩阵的求导。
首先介绍一个符号 \(vec(\mathbf X)\) ,作用是将矩阵 \(\mathbf X\) 按列堆栈来向量化。
解释: vec即将矩阵的每一列取出来然后组成一个列向量,如下:
\[\text{vec}({\pmb{X})}= \left[ x_{11},x_{21},\cdots,x_{m1},x_{12},x_{22},\cdots,x_{m2},\cdots,x_{1n},x_{2n},\cdots,x_{mn} \right]^T
\]
因此,不仅解决了原本的问题,还引入了新的标量与矩阵之间求导方法,如下所示:
1、标量函数对矩阵求导
1.1 行向量偏导形式(又称行偏导向量形式)(分子布局)
即先把矩阵变元 \(\mathbf{X}\) 按 \(vec\) 向量化,转换成向量变元,然后按分子布局求导
\[\begin{align*} \text{D}_{\text{vec}\pmb{X}}f(\pmb{X})&= \frac{\partial f(\pmb{X})}{\partial \text{vec}^T(\pmb{X})} \\\\ &= \left[ \frac{\partial f}{\partial x_{11}},\frac{\partial f}{\partial x_{21}},\cdots,\frac{\partial f}{\partial x_{m1}},\frac{\partial f}{\partial x_{12}},\frac{\partial f}{\partial x_{22}},\cdots,\frac{\partial f}{\partial x_{m2}},\cdots,\frac{\partial f} {\partial x_{1n}},\frac{\partial f}{\partial x_{2n}},\cdots,\frac{\partial f}{\partial x_{mn}} \right] \end{align*}
\]
1.2 \(Jacobian\) 矩阵形式(分子布局)
\[\begin{align*} \text{D}_{\pmb{X}}f(\pmb{X})&= \frac{\partial f(\pmb{X})}{\partial \pmb{X}^T_{m\times n}} \\\\ &= \left[ \matrix{ \frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{21}}&\cdots&\frac{\partial f}{\partial x_{m1}} \\ \frac{\partial f}{\partial x_{12}}&\frac{\partial f}{\partial x_{22}}& \cdots & \frac{\partial f}{\partial x_{m2}}\\ \vdots&\vdots&\vdots&\vdots\\ \frac{\partial f} {\partial x_{1n}}&\frac{\partial f}{\partial x_{2n}}&\cdots&\frac{\partial f}{\partial x_{mn}} } \right]_{n\times m} \end{align*}
\]
1.3 梯度向量形式(又称列向量偏导形式、列偏导向量形式)(分母布局)
即先把矩阵变元 \(\mathbf{X}\) 按 \(vec\) 向量化,转换成向量变元,然后按分母布局求导
\[\begin{align*} \nabla_{\text{vec}\pmb{X}}f(\pmb{X})&= \frac{\partial f(\pmb{X})}{\partial \text{vec}\pmb{X}} \\\\ &= \left[ \frac{\partial f}{\partial x_{11}},\frac{\partial f}{\partial x_{21}},\cdots,\frac{\partial f}{\partial x_{m1}},\frac{\partial f}{\partial x_{12}},\frac{\partial f}{\partial x_{22}},\cdots,\frac{\partial f}{\partial x_{m2}},\cdots,\frac{\partial f} {\partial x_{1n}},\frac{\partial f}{\partial x_{2n}},\cdots,\frac{\partial f}{\partial x_{mn}} \right]^T \end{align*}
\]
1.4 梯度矩阵形式(分母布局)
直接对原矩阵变元每个位置逐个求偏导,结果布局和原矩阵布局一样。
\[\begin{align*} \nabla_{\pmb{X}}f(\pmb{X})&= \frac{\partial f(\pmb{X})}{\partial \pmb{X}_{m\times n}} \\\\ &= \left[ \matrix{ \frac{\partial f}{\partial x_{11}}&\frac{\partial f}{\partial x_{12}}&\cdots&\frac{\partial f}{\partial x_{1n}} \\ \frac{\partial f}{\partial x_{21}}&\frac{\partial f}{\partial x_{22}}& \cdots & \frac{\partial f}{\partial x_{2n}}\\ \vdots&\vdots&\vdots&\vdots\\ \frac{\partial f} {\partial x_{m1}}&\frac{\partial f}{\partial x_{m2}}&\cdots&\frac{\partial f}{\partial x_{mn}} } \right]_{m\times n} \end{align*}
\]
2、矩阵函数对矩阵变元求导
矩阵变元\(\pmb{X}_{m\times n}=(x_{ij})_{i=1,j=1}^{m,n}\),实矩阵函数\(\mathbf F(\mathbf X)\),\(\pmb{F}_{p\times q}=(f_{ij})_{i=1,j=1}^{p,q}\)
2.1 \(Jacobian\) 矩阵形式(分子布局)
即先把矩阵变元 \(\mathbf X\) 按 \(vec\) 向量化,转化为变量变元:
\[\text{vec}({\pmb{X})}= \left[ x_{11},x_{21},\cdots,x_{m1},x_{12},x_{22},\cdots,x_{m2},\cdots,x_{1n},x_{2n},\cdots,x_{mn} \right]^T
\]
即先把实矩阵函数 \(\mathbf F\) 按 \(vec\) 向量化,转化为实向量函数:
\[\text{vec}({\pmb{F}(\pmb{X}))}\\= \left[ f_{11}(\pmb{X}),f_{21}(\pmb{X}),\cdots,f_{p1}(\pmb{X}),f_{12}(\pmb{X}),f_{22}(\pmb{X}),\cdots,f_{p2}(\pmb{X}),\cdots,f_{1q}(\pmb{X}),f_{2q}(\pmb{X}),\cdots,f_{pq}(\pmb{X}) \right]^T
\]
这样,我们就转化为了向量对向量求导,照之前讲过的我们最后即可得到一个 \(pq \times mn\) 的矩阵。
2.2 梯度矩阵形式(分母布局)
与2.1基本相同,先转化为向量求导的形式,然后以分母布局为准即可得到 \(mn \times pq\) 的矩阵。
下面给出以分子布局为标准的展示图(搬运自李沐老师的动手学深度学习):

四、举例求解偏导
一般我们可以通过查阅《The matrix cookbook》得到最终结果,也就是说用那本工具书套用即可,但基本的一些求导我们也要能够理解。
下面举出三个根据定义法求解的例子:
1.求解 \(\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial \mathbf{x}}\)
根据定义,我们先对 \(\mathbf x\) 的第i个分量进行求导,这是一个标量对标量的求导,如下:
\[\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial x_i} = \frac{\partial \sum\limits_{j=1}^n a_jx_j}{\partial x_i} = \frac{\partial a_ix_i}{\partial x_i} =a_i
\]
可见,对向量的第i个分量的求导结果就等于向量 \(\mathbf a\) 的第i个分量。由于我们是分母布局,最后所有求导结果的分量组成的是一个n维向量。那么其实就是向量 \(\mathbf a\)。也就是说:
\[\frac{\partial \mathbf{a}^T\mathbf{x}}{\partial \mathbf{x}} = \mathbf{a}
\]
同样的思路,我们也可以直接得到:
\[\frac{\partial \mathbf{x}^T\mathbf{a}}{\partial \mathbf{x}} = \mathbf{a}
\]
2.求解出 \(\frac{\partial \mathbf{x}^T\mathbf{x}}{\partial \mathbf{x}} =2\mathbf{x}\)
\[\frac{\partial \mathbf{x}^T\mathbf{a}}{\partial \mathbf{x}} = \frac{\partial \sum_{i=1}^{n}x_ix_i}{\partial \mathbf{x}} = \frac{\partial x_i^2}{\partial \mathbf{x}}=\sum_{i=1}^{n}2x_i=2\sum_{i=1}^{n}x_i=2\mathbf x
\]
3.求解出 \(\frac{\partial \mathbf{x}^T\mathbf{A}\mathbf{x}}{\partial \mathbf{x}} = \mathbf{A}^T\mathbf{x} + \mathbf{A}\mathbf{x}\)
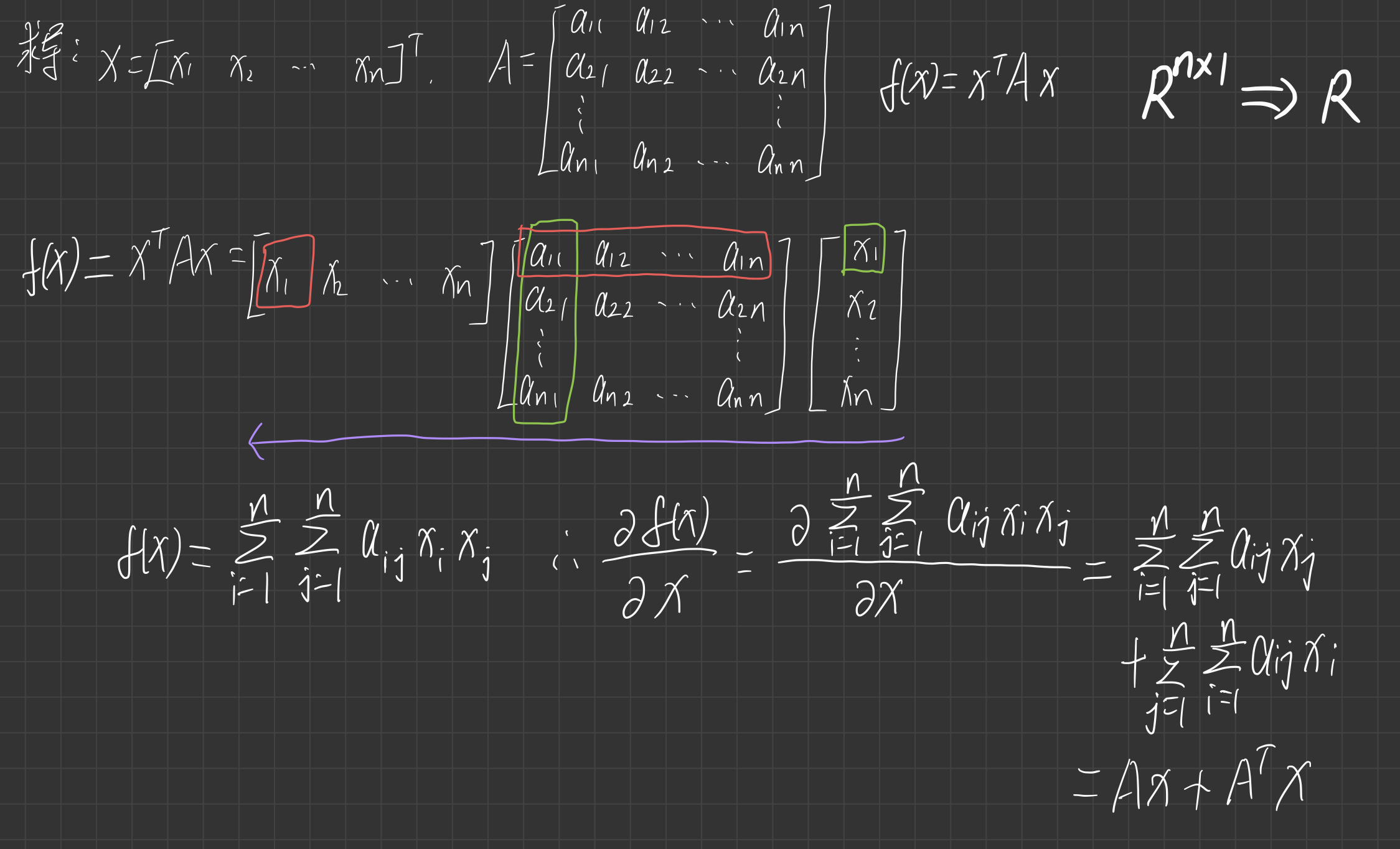
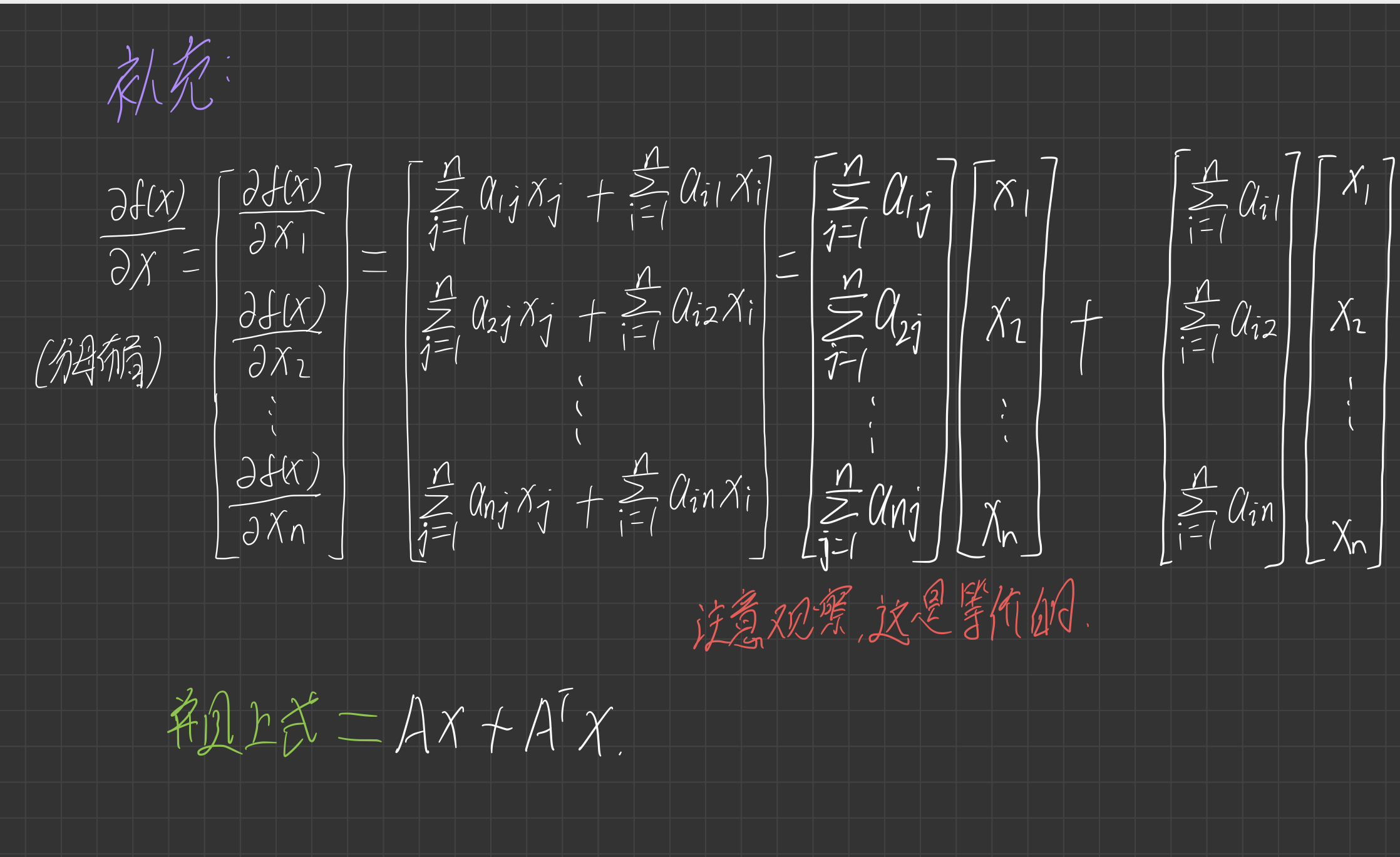
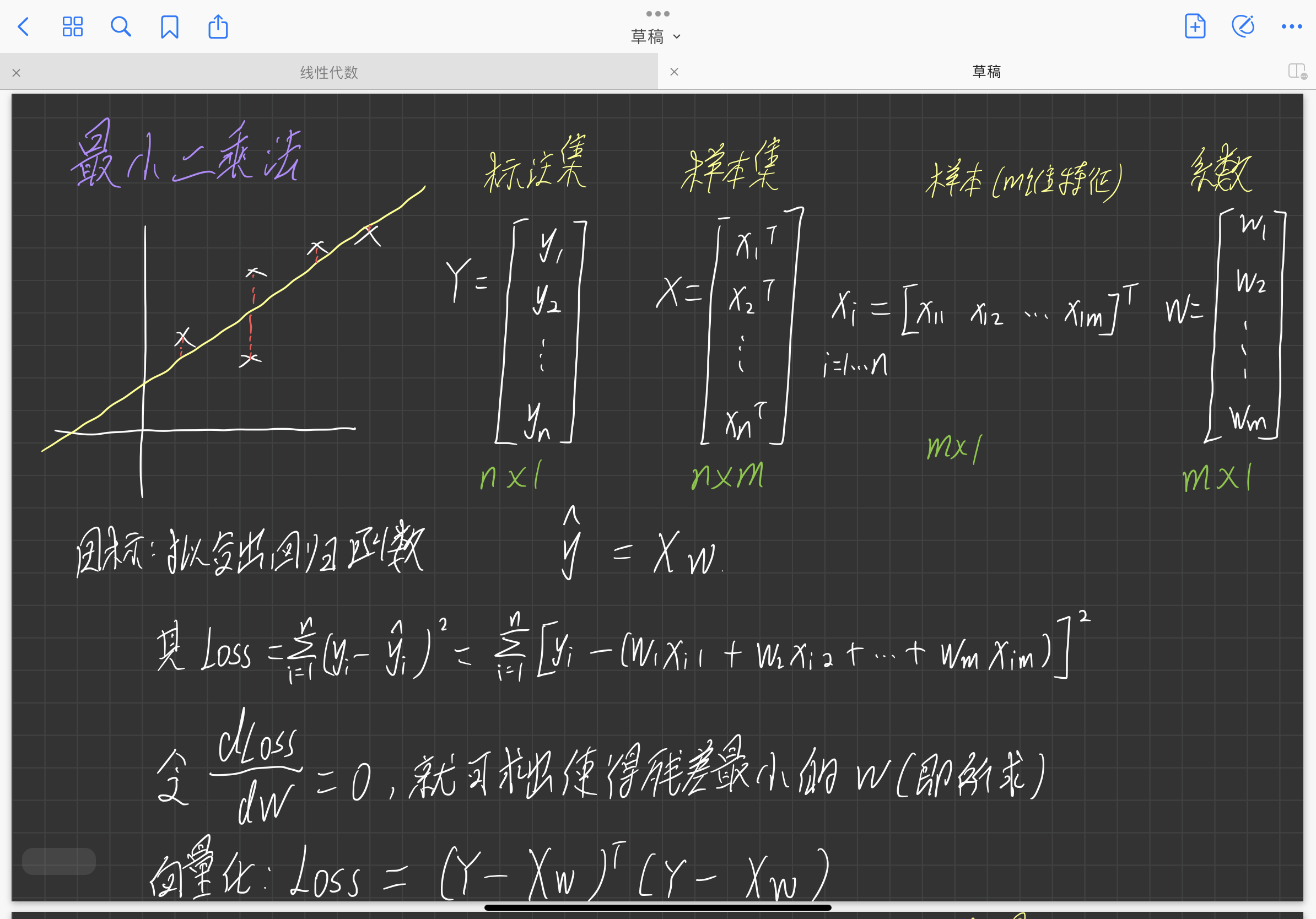
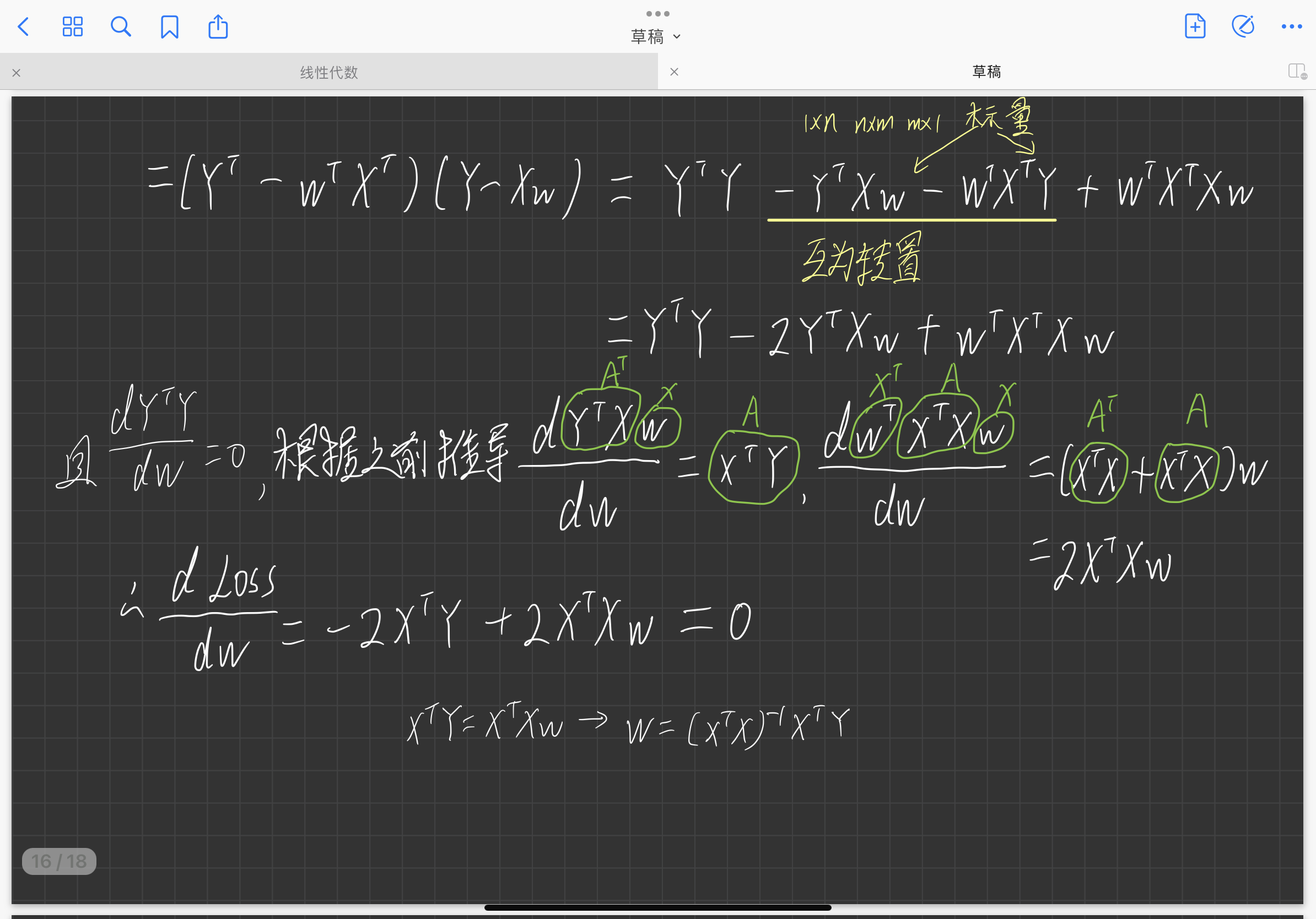
简单的应用实例:最小二乘法