集成学习-偏差与方差

偏差与方差

偏差(Bias)

用所有可能的训练数据集训练出的所有模型的输出的平均值与真实模型的输出值之间的差异。含义：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。

其数学定义为 \(bias^2(x) = (\overline{f}(x) - y)^2\)

方差(variance)

不同的训练数据集训练出的模型输出值之间的差异。含义：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。

其数学定义为
$var(x) = {\mathbb{E}}_{D}[(f(x;D) - \overline{f}(x))^2] $

而泛化误差也就是错误率\(error = bias^2(x) + var(x) + \epsilon^2\),其中\(\epsilon\)为当前学习任务上的噪声。

偏差-方差窘境

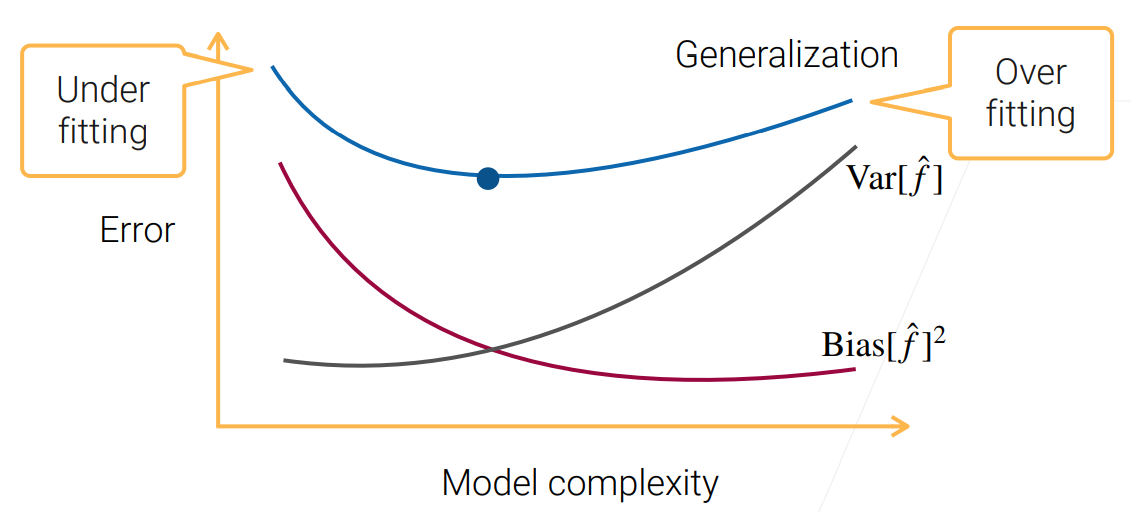
在训练不足时，学习器的拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，此时偏差主导了泛化错误率；随着训练程度的加深，学习器的拟合能力逐渐增强，训练数据发生的扰动渐渐能被学习器学到，方差逐渐主导了泛化错误率；在训练程度充足后，学习器的拟合能力已经非常强，训练数据发生的轻微扰动都会导致学习器发生显著变化，若训练数据自身的、非全局的特性被学习器学到了，则将发生过拟合。

为什么能降低方差

对于每个样本\(x\)，假设在不同数据集上学习得到的模型对样本的输出服从某种分布\(\mathcal{L},G_1(x),G_2(x),\ldots,G_n(x)\)为来自分布独立同分布的随机变量，Bagging的集策略为对弱学习器求平均，即得到模型\(F(x) = \frac{G_1(x)+G_2(x)+\ldots+G_n(x)}{n}\)

设随机变量\(Gi\)的方差为\(\delta^2\),则

\[var(F(x))=Var(\frac{G_1(x)+G_2(x)+\ldots+G_n(x)}{n}) = Var(\frac{G_1(x)}{n}+\frac{G_2(x)}{n}+\ldots+\frac{G_n(x)}{n}) = Var(\frac{\delta^2}{n^2}) * n = \frac{\delta^2}{n}\]

可以看到Bagging集成之后方差变小了，也就是说在不同数据集上训练得到的模型对样本的预测值之间的差距变小。

若各子模型完全相同，而不是完全独立，则

\[Var(F(x))=Var(\frac{G_1(x)+G_2(x)+\ldots+G_n(x)}{n}) = Var(\frac{G_1(x)}{n}+\frac{G_2(x)}{n}+\ldots+\frac{G_n(x)}{n}) = \delta^2\]

此时并不会降低variance。bagging方法得到的各子模型是有一定相关性的，属于上面两个极端状况的中间态，因此可以一定程度降低variance。但对于Adaboost来说，其子模型之间是强相关的，因此子模型之和并不能显著降低variance。

为什么偏差不变

因为Bagging中的子样本集具有相似性，因此各模型有近似相等的bias，由于模型之间虽不完全独立，但模型之间也没有强依赖关系，\(E[\frac{\sum {X_i}}{n}] = E[X_i]\)
因此单个模型和集成之后的模型关于样本的预期值差别不大，bias也近似。而对于Boosting，其训练好一个弱分类器之后计算错误作为下一个分类器的输入，这个过程本身就是在不断减小损失函数，来使得模型偏差不断降低。