7.30 背包问题
1 01背包
问题描述:
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
基本思路 :
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
顺序写:
for(int i=1;i<=n;i++) { for(j=c[i];j<=v;j++) //容量至少要大于c[i]啊,不然就只能不选i了 { f[i][j]=max(f[i-1][j],f[i-1][j-c[i]]+w[i]);//选与不选中找大的那一个 } }
这样写要开二维数组,浪费空间
怎么节省空间呢?
观察上面的状态转移方程,可以发现
f[i][j](放前i个物品,容量为j时的最大价值)=max(f[i-1][j](不放第i个物品的上一个状态的价值),f[i-1][j-c[i]]+w[i](放了第i个物品的上一个状态的价值加上 i 物品的价值))
所以我们只要保证我们找到的都是上一个状态即可。
化简为一维数组->f[j] 显然f[j]=max (f[j],f[j-c[i]]+w[i]) 显然括号里的f[j]为上一个状态,那么我们还要保证f[j-c[i]]为上一个状态,如果顺序求,求到f[j]时,f[j-c[i]]已经被更新过了,就不再是上一个状态
所以我们逆序求,保证下标小的未被更新即可
f[v]即是最大的价值
for(int i=1;i<=n;i++) { for(j=v;j>=c[i];j--) { f[j]=max(f[j],f[j-c[i]]+w[i]);
} }

2 完全背包
问题描述:有编号分别为a,b,c,d的四件物品,它们的重量分别是2,3,4,7,它们的价值分别是1,3,5,9,每件物品数量无限个,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
完全背包问题与01背包问题的区别在于每一件物品的数量都有无限个,而01背包每件物品数量只有一个。
之前对于01背包逆序求的解释还有一种,即拿完一个就没得了,f[i][j]=max(f[i-1][j],f[i-1][j-c[i]]+w[i] (拿第i个,上一个状态只能拿前i-1个)
而完全背包拿完了还可以再拿,f[i][j]=max(f[[i-1][j] (不拿第i个),f[i][j-c[i]]+w[i] (拿第i个,上一个状态可能仍旧拿的是第i个)
如此对于完全背包,我们不需要保证得到的都是之前的状态,顺序求即可
for(int i=1;i<=n;i++) { for(j=c[i];j<=v;j++) { f[j]=max(f[j],f[j-c[i]]+w[i]); } }
3 多重背包
多重背包在完全背包的基础上加上了第i件物品最多只有m[i]件的限制
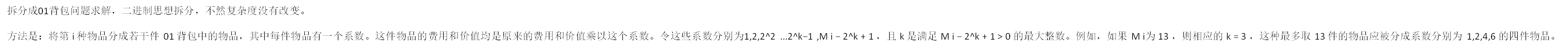
int num=0; for(int i=1;i<=n;i++) { int k=1; while(k<m[i]) { w[num]=pw[i]*k; c[num]=pc[i]*k; num++; m[i]-=k; k<<=1; } w[num]=pw[i]*m[i]; c[num]=pc[i]*m[i]; num++; } F[0-v]=0; for(int i=0;i<num;i++) { for(int j=v;j>=c[i];j--) { F[j]=max(F[j],F[j-c[i]]+w[i]); } }
4 混合背包
模板
当第i个物品的价值乘以它最多可用的件数大于背包容量时,把它当成完全背包即可(对于物品i来说这个背包就是完全背包因为它肯定用不完)
int p[MAXN];//质量 int h[MAXN];//价值 int c[MAXN];//个数 int dp[MAXN]; void zero(int v,int c,int w) { for(int i=v;i>=c;i--) dp[i]=max(dp[i],dp[i-c]+w); } void cp(int v,int c,int w) { for(int i=c;i<=v;i++) dp[i]=max(dp[i],dp[i-c]+w); } int mul(int n,int v) { memset(dp,0,sizeof dp); for(int i=1;i<=n;i++) { if(p[i]*c[i]>=v) { cp(v,p[i],h[i]); continue; } int k=1; while(k<c[i]) { zero(v,k*p[i],k*h[i]); c[i]-=k; k*=2; } zero(v,c[i]*p[i],c[i]*h[i]); } return dp[v]; }
5 分组背包


类似于01背包
for(i=1;i<=n;i++) //遍历每一组 { for(j=m;j>=0;j--) //每一组的容量为j { for(k=1;k<=j;k++) //从每一组的第一个元素遍历到这一组的容量 { f[j]=max(f[j],f[j-k]+a[i][k]); } } }
6 二维费用背包

此题模板根据题目改动即可
状态转移方程

for(i=1; i<=m; ++i)//忍耐度 for(j=0; j<K; ++j)//怪的种数 for(k=1; k<=s; ++k) //可杀怪总数 if(w[j]<=i)dp[i][k]=max(dp[i][k],dp[i-w[j]][k-1]+v[j]);
A题:
Description
今天AveryBoy去一家诡异的店买东西。如果卡上的余额>=5,就一定可以买到东西,即使买完之后卡上余额为负;否则不能买到东西,即使卡上的余额足够。所以最后大家肯定都希望卡上的余额尽可能的少。
现在已知商店有n种商品并且每种商品只有一个,每种商品的价格和卡上余额,求最少能使卡上余额为多少?
Input
有多组输入数据,对于每组输入数据:
第一行为一个正整数n,n<=1000,表示商品的个数。
第二行为n个正整数,表示每种商品的价格,价格<=50。
第三行为一个正整数m,m<=1000,表示卡上的余额。
n=0表示输入结束。
Output
Sample Input
1
50
5
10
1 2 3 2 1 1 2 3 2 1
50
0
Sample Output
-45
32
HINT
此题对于01背包做了一点小改变
我们只有使最后一次买的商品价值最大才可能让卡上的余额最小
所以我们对商品价值排序
当卡上余额大于5时,我们先减去5,保证最后一次买价值最大的商品可以进行
然后对于剩下的n-1个物品,剩下的余额套用01背包模板即可 求出不超过余额(容量)的最大价值

#include <bits/stdc++.h> using namespace std; int p[1100],f[1100]; int main() { while(1) { int n,m; scanf("%d",&n); if(n==0)break; int i,j; for(i=1;i<=n;i++)scanf("%d",&p[i]); scanf("%d",&m); if(m<5)printf("%d\n",m); else { sort(p+1,p+n+1); m-=5; memset(f,0,sizeof f); for(i=1;i<n;i++) { for(j=m;j>=p[i];j--) { f[j]=max(f[j],f[j-p[i]]+p[i]); } } printf("%d\n",m+5-f[m]-p[n]); } } return 0; }
B题:
Input
Output
Sample Input
10 10 1 10
1 1
10 10 1 9
1 1
9 10 2 10
1 1
2 2
Sample Output
0
-1
1
HINT
二维费用背包

// hdu 2159 #include <cstdio> #include <cstdlib> #include <cstring> #include <cmath> #include <iostream> using namespace std; int dp[105][105],a[105],b[105]; int main() { int n,m,k,s,tmp; while(~scanf("%d%d%d%d",&n,&m,&k,&s)) { for(int i=1;i<=k;i++) scanf("%d%d",&a[i],&b[i]); memset(dp,0,sizeof(dp)); tmp=0; for(int i=1;i<=m;i++) { for(int j=1;j<=k;j++) { if(i<b[j]) continue; for(int x=1;x<=s;x++) { for(int y=1;y<=x&&y*b[j]<=i;y++) { dp[i][x] = max(dp[i-y*b[j]][x-y]+y*a[j],dp[i][x]); } } } if(dp[i][s]>=n) { tmp=i; break; } } if(tmp==0) printf("-1\n"); else printf("%d\n",m-tmp); } return 0; }
也可以用完全背包,判断条件即可

#include<bits/stdc++.h> using namespace std; const int inf=1e9; int w[110],c[110],f[110],t[110]; int n,m,k,s; int main() { while(~scanf("%d%d%d%d",&n,&m,&k,&s)) { int i,j; for(i=1;i<=k;i++)scanf("%d%d",&w[i],&c[i]); memset(f,0,sizeof f); memset(t,0,sizeof t); int ans=inf; for(i=1;i<=k;i++) { for(j=c[i];j<=m;j++) { if(f[j]<f[j-c[i]]+w[i]&&t[j-c[i]]<s) { f[j]=f[j-c[i]]+w[i]; t[j]=t[j-c[i]]+1; } if(f[j]>=n&&j<ans) { ans=j; } } } if(ans==inf)printf("-1\n"); else printf("%d\n",m-ans); } return 0; }
C题:
Input
Output
Sample Input
1
8 2
2 100 4
4 100 2
Sample Output
400
HINT
混合背包模板

#include<bits/stdc++.h> using namespace std; #define MAXN 105 int p[MAXN];//质量 int h[MAXN];//价值 int c[MAXN];//个数 int dp[MAXN]; void zero(int v,int c,int w) { for(int i=v;i>=c;i--) dp[i]=max(dp[i],dp[i-c]+w); } void cp(int v,int c,int w) { for(int i=c;i<=v;i++) dp[i]=max(dp[i],dp[i-c]+w); } int mul(int n,int v) { memset(dp,0,sizeof dp); for(int i=1;i<=n;i++) { if(p[i]*c[i]>=v) { cp(v,p[i],h[i]); continue; } int k=1; while(k<c[i]) { zero(v,k*p[i],k*h[i]); c[i]-=k; k*=2; } zero(v,c[i]*p[i],c[i]*h[i]); } return dp[v]; } int main() { int T; cin>>T; while(T--) { int v,n; cin>>v>>n; for(int i=1;i<=n;i++) { cin>>p[i]>>h[i]>>c[i]; } cout<<mul(n,v)<<endl; } return 0; }
D题:
Description
Input
输入包含多组测试数据,每组测试数据第一行是两个正整数n,m。表示课程数和他学习的天数。
之后是n*m的矩阵,A[i][j]表示第i门课程学习j天会获得的分数。(1<=i<=n<=100,1<=j<=m<=100,1<=A[i][j]<=50)
输入以n=0,m=0结束。
Output
Sample Input
2 2
1 2
1 3
2 2
2 1
2 1
2 3
3 2 1
3 2 1
0 0
Sample Output
3
4
6
HINT
分组背包问题
把每种课当成一个组(只能选择一个天数对应的分数)

#include<bits/stdc++.h> using namespace std; int a[110][110],f[110]; int main() { int n,m; while(1) { scanf("%d%d",&n,&m); if(n==0&&m==0)break; int i,j,k; for(i=1;i<=n;i++) { for(j=1;j<=m;j++) { scanf("%d",&a[i][j]); } } memset(f,0,sizeof f); for(i=1;i<=n;i++) //遍历每一组 { for(j=m;j>=0;j--) //每一组的容量为j { for(k=1;k<=j;k++) //从每一组的第一个元素遍历到这一组的容量 { f[j]=max(f[j],f[j-k]+a[i][k]); } } } printf("%d\n",f[m]); } return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号