深度学习中的LOSS
【总结】深度学习中的损失函数
1. 铰链损失/合页损失 Hinge Loss
SVM常用损失函数
-
函数表达式
\(L(y,f(x)) = max(0,1-y·f(x))\) -
函数图像
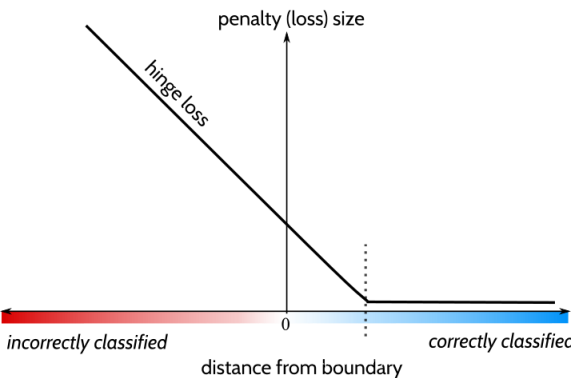
通过上图可知,当\(y·f(x)>1\)时,\(loss=0\);否则,\(loss=1-y·f(x)\)。也就是说,只有被正确分类的时候,loss才为0。
2. 交叉熵 Cross-entropy Loss
(1)用于二分类
表示样本abel与预测值为正类概率的关系
- 函数表达式
\(C = -\frac{1}{N}\sum_i[y_iln(p_i)+(1-y_i)ln(1-p_i)]\)
其中,
\(y_i\)——样本\(i\)的label,正类为1,负类为0;
\(p_i\)——样本\(i\)的预测值为正类的概率。
(2)用于多分类
-函数表达式
\(C = -\frac{1}{N}\sum_i\sum_k[y_{ik}ln(p_{ik})]\)
其中,
\(y_{ik}\)——样本\(i\)的label,与正类类别相同为1,否则为0;
\(p_{ik}\)——样本\(i\)的预测值为第\(k\)类的概率。
- 优点
使用逻辑函数得到概率,并结合交叉熵当损失函数时,在模型效果差的时候学习速度比较快,在模型效果好的时候学习速度变慢 - 缺点
sigmoid(softmax)+cross-entropy loss 擅长于学习类间的信息,因为它采用了类间竞争机制,它只关心对于正确标签预测概率的准确性,忽略了其他非正确标签的差异,导致学习到的特征比较散。基于这个问题的优化有很多,比如对softmax进行改进,如L-Softmax、SM-Softmax、AM-Softmax等。
3. 均方误差MSE
- 函数表达式
\(MSE = \frac{1}{n}\sum_i^n(\hat{y_i}-y_i)^2\) - 缺点
逻辑回归配合MSE损失函数采用梯度下降法进行学习时,在训练初始阶段学习速率非常慢
4. Smooth L1 Loss
- 函数表达式
\[smooth_{L_1}(x) = \begin{cases}
0.5x^2, & |x| <1 \\
|x| - 0.5, & otherwise
\end{cases}\]
- 函数图像
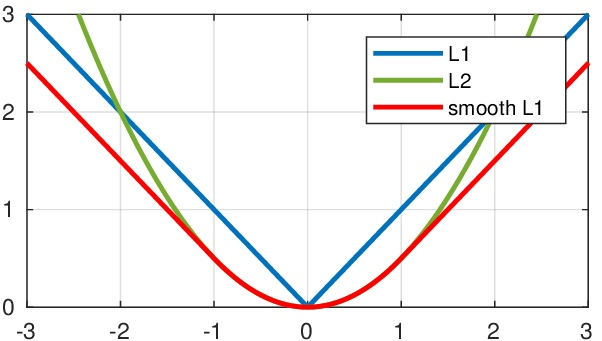
参考
(1) 机器之心——机器学习大牛最常用的5个回归损失函数,你知道几个?
(2) 一文读懂机器学习常用损失函数(Loss Function)
(3) 损失函数 - 交叉熵损失函数


