E - Fibonacci Again（找规律）

逐渐发现找规律的美妙之处啦，真不错，用普通方法解决很久或者很麻烦的问题，找到规律就很方便，算法最主要还是思想

Description

There are another kind of Fibonacci numbers: F(0) = 7, F(1) = 11, F(n) = F(n-1) + F(n-2) (n>=2). 

 

Input

Input consists of a sequence of lines, each containing an integer n. (n < 1,000,000). 

 

Output

Print the word "yes" if 3 divide evenly into F(n). 

Print the word "no" if not. 

 

Sample Input

0 1 2 3 4 5

 

Sample Output

no no yes no no no

 

问题描述：

　　对于以7， 11，为f(0)和f(1)的斐波那契数列，f(n) = f(n-1) + f(n-2);

　　输入项数n，问第n项是否能被三整除

 

这样一个斐波那契数列很大很大，特别是测试项数还比较多，用大数存储也能做，但是比较麻烦，可以打表找规律

打表代码：

#include <stdio.h>
long long a[100];
void init()
{
    a[0] = 7;
    a[1] = 11;
    for(int i = 2; i < 100; i++)
    {
        a[i] = a[i-1]+a[i-2];
    }
}
int main()
{
    init();
    for(int i = 0; i < 100; i++)
    {
        printf("a[%d] = %lld\n", i, a[i]);
        if(a[i] % 3 == 0)
            printf("*****\n");
    }
    return 0;
}

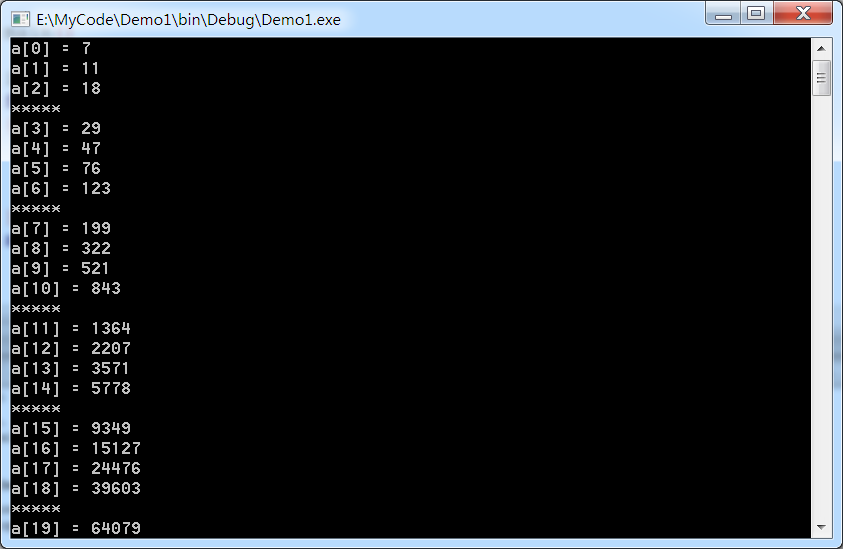
发现每四项有一个满足要求的，所以代码如下：

#include <stdio.h>

int main()
{
    long long n;
    while(scanf("%lld", &n)!= EOF)
    {
        if(n % 4 == 2)
            printf("yes\n");
        else
            printf("no\n");
    }
    return 0;
}